MATLAB 使用记录 ¶
约 4732 个字 316 行代码 预计阅读时间 22 分钟
MATLAB 是“matrix laboratory”的缩写形式。MATLAB® 主要用于处理整个的矩阵和数组,而其他编程语言大多逐个处理数值。矩阵是指通常用来进行线性代数运算的二维数组。
软件配置 ¶
Matlab in VSCode¶


下载插件
在 python 环境中,最好 3.9
import sys
print(sys.maxsize > 2**32)
找到安装 matlab 的 root 路径
\extern\engines\python进入放置setup.py的位置;
python setup.py install
ipython
import matlab.engine
eng = matlab.engine.start_matlab()
eng.sqrt(4.0)

注意这里如果使用 conda 环境,需要配置对应的 conda 中的 python 路径
配好了以后右上角就会有执行代码的按钮了
小 bug ¶
- 需要 vscode 打开
.m文件的文件夹,否则会报错
基础 ¶
Ctrl + I自动整理缩进
多行注释:选中多行 → Ctrl+R;
取消多行注释:选中多行 → Ctrl+T。
format long
复数 ¶
复数包含实部和虚部,虚数单位是 -1 的平方根。
sqrt(-1)
ans = 0.0000 + 1.0000i
要表示复数的虚部,请使用 i 或 j。
c = [3+4i, 4+3j; -i, 10j]
字符串数组中的文本 ¶
当您处理文本时,将字符序列括在双引号中。可以将文本赋给变量。
t = "Hello, world";
如果文本包含双引号,请在定义中使用两个双引号。
q = "Something ""quoted"" and something else."
有时,字符表示的数据并不对应到文本,例如 DNA 序列。您可以将此类数据存储在数据类型为 char 的字符数组中。字符数组使用单引号。
seq = 'GCTAGAATCC';
whos seq
seq2 = [seq 'ATTAGAAACC']
seq2 =
'GCTAGAATCCATTAGAAACC'
变量 ¶
使用 whos 可以查看工作区的内容。
whos
退出 MATLAB 后,工作区变量不会保留。使用 save 命令保存数据以供将来使用,
save myfile.mat
通过保存,系统会使用 .mat 扩展名将工作区保存在当前工作文件夹中一个名为 MAT 文件的压缩文件中。
要清除工作区中的所有变量,请使用 clear 命令。
使用 load 将 MAT 文件中的数据还原到工作区。
load myfile.mat
函数 ¶
max()
union()
[minA,maxA] = bounds(A) % 如果存在多个输出参数,请将其括在方括号中
用引号将任何文本输入括起来:
disp("hello world")
输出 ¶
disp()¶
A = [1 0];
disp(A)
S = 'Hello World.';
disp(S)
fprintf()¶
fprintf('X is %4.2f\n',A)
print()¶
bar(1:10)
print
矩阵 ¶
创建 ¶
请使用逗号 ( , ) 或空格分隔各元素 , 使用分号分隔各行。
创建矩阵的另一种方法是使用 ones、zeros 或 rand 等函数。
a = [1 3 5; 2 4 6; 7 8 10]
z = zeros(5,1)
eye(size(A)) %产生与A矩阵同阶的单位矩阵
zeros()
ones() % 产生0和1的矩阵
rand() % 产生随机元素的矩阵
diag() % 产生对角矩阵
triu() % 产生上三角矩阵
tril() % 产生下三角矩阵
size() %显示一个包含两个元素的向量:矩阵的行与列的个数。函数length()返回向量的长度或矩阵行数和列数的最大值
取值 ¶
A(4,2)
A(8) % 单一下标按顺序向下遍历每一列
A(1:3,2) % 列出 A 前三行及第二列中的元素,与python元组语法类似
A(3,:)
B = 0:10:100 % 冒号表达式
运算 ¶
MATLAB 允许您使用单一的算术运算符或函数来处理矩阵中的所有值
a + 10
sin(a)
a' % 转置
inv(a) % 逆矩阵
您可以使用 * 运算符执行标准矩阵乘法
p = a*inv(a)
元素级别乘法
p = a.*a
a.^3
乘方
A^P
矩阵值 ¶
方阵的行列式:det
矩阵的迹: trace
矩阵的秩: rank
矩阵和向量的范数
- norm 欧几里德范数
- norm(x,inf) 无穷范数
矩阵函数
expm logm sqrtm
串联 ¶
串联是连接数组以便形成更大数组的过程。实际上,第一个数组是通过将其各个元素串联起来而构成的。成对的方括号 [] 即为串联运算符。
A = [a,a]
A = [a; a] % 垂直
分解 ¶
LU¶
矩阵的三角分解:将一个方阵表示为一个上三角阵(U)和一个下 三角阵(L)的乘积(LU分解)
[L,U]=lu(X)
QR¶
矩阵的正交变换:分解为正交矩阵(Q)和上三角矩阵(R)的乘积 (QR分解)
[Q,R]=qr(A)
特征值分解 ¶
eig(A) 以列向量形式返回特征值,[X,D]=eig(A)返回
特征值和特征向量,D为特征值对角阵,特征向量X。
SVD¶
奇异值分解
[U,S,V]=svd(A)
信号处理 ¶
conv() % 卷积
laplace(x) % 拉普拉斯变换
连续系统时域分析 ¶
sys = tf(num,den)
# 单位冲激响应
[y,t] = impulse(sys)
[y,t] = impulse(sys,T_final)
# 单位阶跃响应
[y,t] = step(sys)
[y,t] = step(sys,Tfinal)
# 任意激励 lsim
[y,t,x] = lsim(sys,u,t)
[y,t,x] = lism(sys,u,t,x_0) %x_0系统状态变量
离散系统时域分析 ¶
# 单位脉冲响应
[h,t] = impz(num,den)
impz(b,a,-3:10)
# 单位阶跃响应
[h,t] = stepz(num,den)
# 零状态响应
y = filter(num,den,x,zi)
% x是包含输入序列非零样值点,zi表示系统输入延时
[y,x] = dlism(num,den,u,x0)
频域分析 ¶
时域卷积对应频域相乘
连续系统:\(Y(\omega) = X(\omega)H(\omega)\)
离散系统:\(Y(\Omega) = X(\Omega)H(\Omega)\)
# 连续系统频率特性
[h,w] = freqs(sys,n) % n为输出频率点个数
abs() % 幅频
angle() % 相频
#
heaviside(t) 单位冲激响应h(t)
fourier(x) % 傅里叶变换
ifourier(Y) % 傅里叶反变换
# 离散系统频率特性
[h,w] = freqz(sys, n, Fs) %频率等分点向量w的采样频率Fs,省略时候,w为0-pi的n个频率等分点
[h,w] = freqz(sys,n,'whole') % H(Ω) 0-2pi n个频率等分点
复频域分析 ¶
连续系统 ¶
# 传递函数表达方式转换
[z,p,k] = tf2zp(num,den)
[num,den] = tf2tf(z,p,k)
[N,D] = numden(A) % 多项式分解成分子多项式N,分母多项式D
a = sym2pol(P) % 返回多项式系数向量
# 求根
r = roots(N)
N = poly(r) % 将根转换为多项式系数向量
den = conv() % 将因子相乘形式转换为多项式形式
# 部分分式展开
[r,p,k] = residue(num,den)
# 绘制零极点分布
pzmap(sys)
离散系统 ¶
zrans(x)
[r,p,k] = residuez(num,den)
# 绘制图像
zplane(num,den)
Simulink¶
- 系统仿真:Simulink 是 MATLAB 中用于动态系统建模、仿真和分析的工具箱,可以用于自动控制原理课程中的系统仿真。
- 控制系统设计:通过 Simulink,可以设计和分析各种类型的控制系统,包括反馈控制系统、前馈控制系统等。
使用方法:在 matlab 中输入simulink,打开 simulink 模型编辑器。
快捷键 ¶
Ctrl + R:顺时针旋转Ctrl + Shift + R逆时针旋转- 按住
Ctrl键并连接线,可以从一条线中分支 Ctrl + M:打开 maskCtrl + Shift + X注释Ctrl + G创建子系统Ctrl + Shift + G取消创建子系统
常用元件 ¶
mux:多路复用器,可以实现多个输入信号的选择
scope:示波器,用于显示信号波形;设置里可以更改输入端口的个数;
如果看不到曲线的话,检查一下是不是坐标轴范围给的太大了
transfer function:传递函数,用于建立系统的传递函数模型
step:阶跃信号,用于产生阶跃信号
add:加法器,用于实现信号的加法运算;设置里可以更改输入端口的个数
Saturation 限幅
PID¶
改进型 ¶
当系统容易收到高频信号的干扰时 , 微分作用会将高频信号的扰动放大 ( 自控课本上说的 ), 高频信号变化的较快 , 而微分是去求误差的变化率 , 所以有高频扰动信号 , 就会被微分作用给放大 , 建议对微分环节做低通滤波 , 通常是一阶低通滤波
微分环节的缺点,就是误差 e 变化微弱的时候,如果 D 过大会产生过大的修正量,导致震动不但不减小反而扩大。 滤波器的作用就是滤除高频修正,使D更好用,说白了是一个改进型,
积分饱和 ¶
那么什么时候需要加积分环节限制输出呢?当系统在抗扰动时,需要一个大的 Ki 参数来快速消除稳态误差,而在开始从 0 到稳态这个过程又会因为 ki 太大而引起过大超调时,这个时候就需要加积分过饱和限制。
使用外部参数 ¶
PID 自动调参 ¶
点击自动调节
调节最上方的响应时间和瞬态特性,可以得到不同的曲线 按照自己项目的要求对应的调整
调整之后,点击“更新模块”,就会换成新的 PID 参数
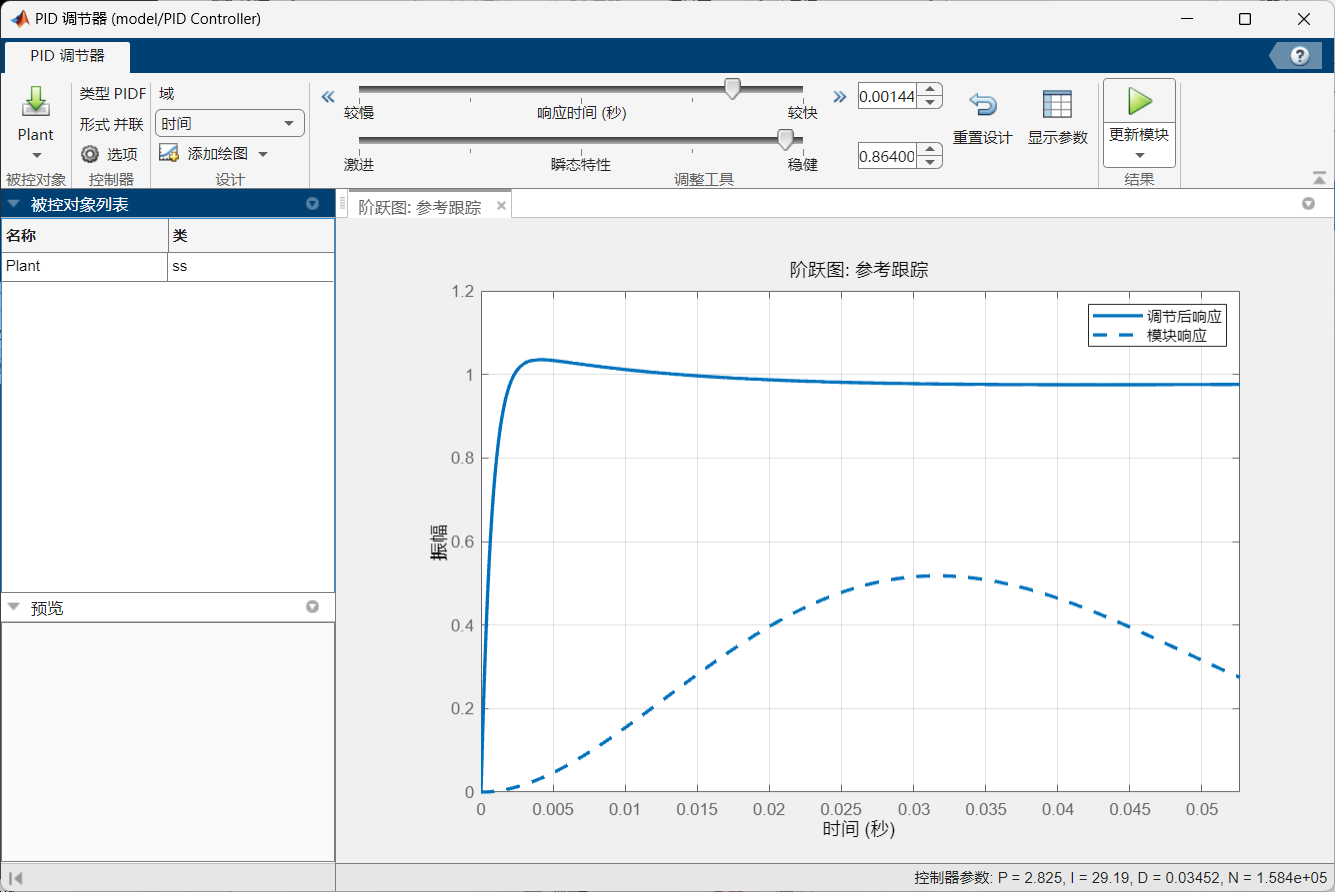
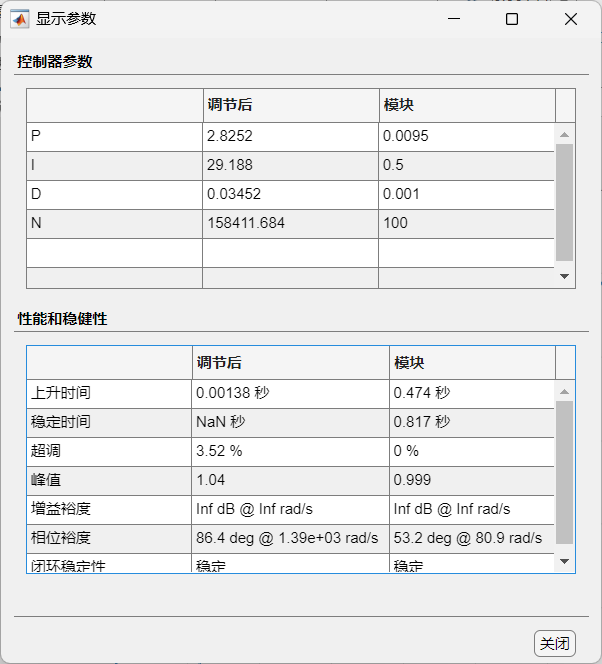
点击“显示参数”,可以查看 PID 参数
S function¶
S function 就是自定义的模型,用于补充 simulink 中没有的功能
S-function 入门及案例详解(1)——S-function 基础介绍及基本案例 -CSDN 博客
S-function 入门及案例详解(2)——S-function 基本案例介绍 _s-function 怎么用 -CSDN 博客
S-function 入门及案例详解(3)——S-function 进阶案例 _s 函数 英文学习指导 -CSDN 博客
S-function 入门及案例详解(4)——S-function 进阶案例之连续 / 离散状态空间表达式的 S-function 实现 _s-function 实例 -CSDN 博客
S-function 模块,位于 Simulink/User-Defined Functions 模块库中,是使 S-function 图形化的模板工具,用于为 S-function 创建一个定值的对话框和图标。

S-function name:填入 S-function 的函数名称,这样就建立了 S-function 模块与 M 文件形式的 S-function 之间的对应关系;
S-function parameters:填入 S-function 需要输入的外部参数的名称,如果有对各变量,则变量中间用逗号隔开,如 a,b,c;
S-function modules:仅当 S-function 是用 C 语言编写并用 MEX 工具编译的 C-MEX 文件时,才需要填写该参数;
直接馈通
如果输出函数(mdlOutputs 或 flag==3)是输入 u 的函数,即,如果输入 u 在 mdlOutputs 中被访问,则存在直接馈通。ex:\(y= k\cdot u\)
采样时间与偏移量
采样时间是按照固定格式成对指定的:[采样时间 偏移时间]。
| 采样时间表示 | 意义 |
|---|---|
| [0 0] | 连续采样时间 |
| [-1 0] | 继承 S-function 输入信号或父层模型的采样时间 |
| [0.5 0.1] | 离散采样时间,从 0.1s 开始每 0.5s 采样一次 |
函数分析 ¶
S-function 包括主函数和 6 个功能子函数,包括 mdlInitializeSizes(初始化
在 S-function 仿真过程中,利用 switch-case 语句,根据不同阶段对应的 flag 值(仿真流程标志向量)来调用 S-function 的不同子函数,以完成对 S-function 模块仿真流程的控制。

Mask¶
如果我们不想每次修改 S-function 的参数都要打开 S-function 的编辑窗口,我们可以使用 Mask 功能。
第一步是增加 Mask
点击添加封装
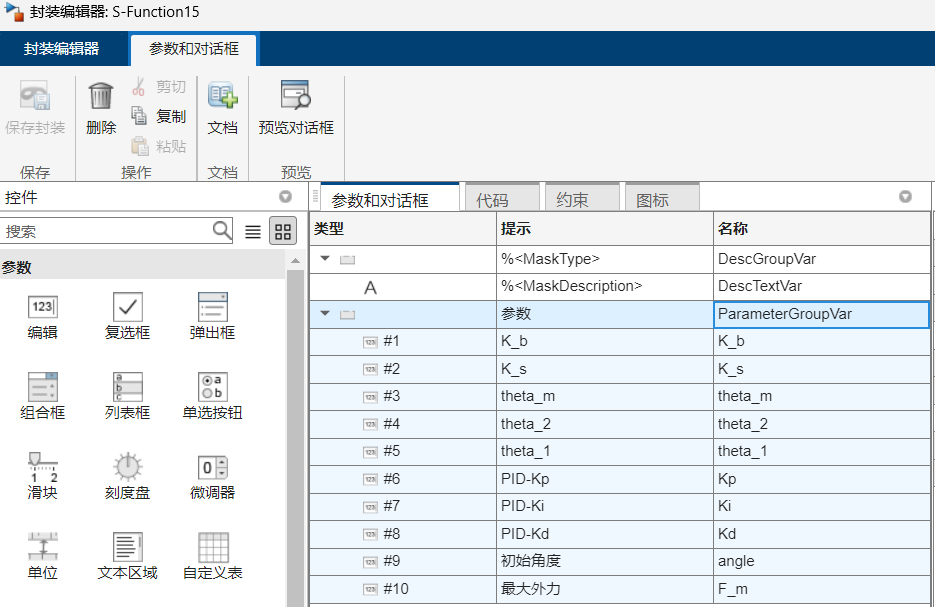
提示框可以随便写,但是名称需要和代码中的变量名称对齐。
第二步是在 S-function 初始化当中加入 Mask 参数
```matlab hl_lines="1,3,8,20" function [sys,x0,str,ts,simStateCompliance] = expert_control(t,x,u,flag,K_b,K_s,theta_m,theta_2,theta_1,Kp,Ki,Kd,angle,F_m) switch flag case 0 [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes(angle); case 1 sys=mdlDerivatives(t,x,u); case 2 sys=mdlUpdate(t,x,u,K_b,K_s,theta_m,theta_2,theta_1,Kp,Ki,Kd,F_m); case 3 sys=mdlOutputs(t,x,u); case 4 sys=mdlGetTimeOfNextVarHit(t,x,u); case 9 sys=mdlTerminate(t,x,u); otherwise DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag)); end
%% 子函数定义部分 function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes(angle)
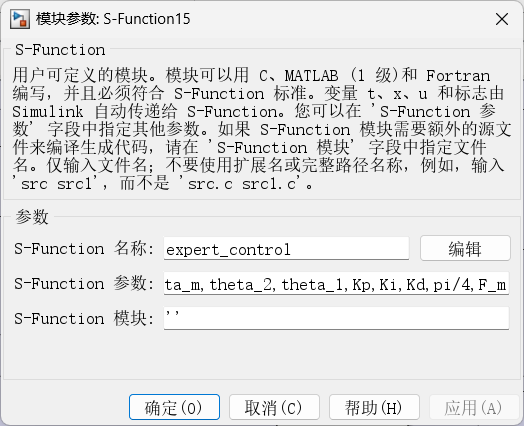
**第三步是在s-function的模块参数中,添加需要预置的参数**
在参数这一行把需要的参数填进去,按照顺序来
## Control System Toolbox
### 构建系统模型
#### 传递函数 `tf()`
$$
G(s) = \frac{Y(s)}{U(s)}
$$
传递函数法可以通过`tf`函数来实现,其基本语法为:
```matlab
sys = tf(num, den)
其中,num和den分别是传递函数的分子和分母多项式系数向量。
状态空间ss() | state space ¶
其中,\(x(t)\) 是系统的状态向量,\(u(t)\) 是系统的输入,\(y(t)\) 是系统的输出,\(A\)、\(B\)、\(C\)、\(D\)是系统矩阵。
状态空间法可以通过ss函数来实现,其基本语法为:
sys = ss(A, B, C, D)
其中,A、B、C、D分别是状态空间模型的状态矩阵、输入矩阵、输出矩阵和直接传输矩阵。
示例代码:
A = [0, 1; -1, -2];
B = [0; 1];
C = [1, 0];
D = 0;
sys = ss(A, B, C, D);
这将创建一个状态空间模型sys,其状态空间表示为:
频率响应法freqs() ¶
频率响应法是一种基于频率特性的分析方法,通过建立系统的频率响应函数来描述系统的输入输出关系。
其中,\(G(j\omega)\) 是系统的频率响应函数,\(Y(j\omega)\) 是系统的输出,\(U(j\omega)\) 是系统的输入,\(j\) 是虚数单位,\(\omega\)是角频率。
频率响应法可以通过freqs函数来计算系统的频率响应,其基本语法为:
[H, w] = freqs(num, den)
其中,H是系统的频率响应,w是对应的频率向量。
示例代码:
num = [1, 2];
den = [1, 3, 2];
[H, w] = freqs(num, den);
这将计算传递函数G(s) = (1 + 2s)/(1 + 3s + 2s^2)的频率响应H和对应的频率向量w。
零极点法zpk(z,p,k) ¶
零极点法是一种基于零极点的分析方法,通过确定系统的零点和极点来描述系统的频率特性。零极点模型可以表示为:
其中,\(b_0, b_1, \cdots, b_n\) 是系统的零点,\(a_0, a_1, \cdots, a_m\)是系统的极点。
零极点法可以通过zpk函数来实现,其基本语法为:
sys = zpk(z, p, k)
其中,z、p、k分别是系统的零点、极点和增益。
示例代码:
z = [-1];
p = [-2, -3];
k = 2;
sys = zpk(z, p, k);
这将创建一个零极点模型sys,其传递函数为:
连续系统离散化 ¶
SYSD = c2d(SYSC,Ts,METHOD)
METHOD缺省为采用零阶保持器的方法,Ts为采样周期。
Method:
- zoh——采用零阶保持器
- foh——采用一阶保持器
- tustin——采用双线形(tustin)逼近方法
- prewarp——采用改进的tustin方法
- matched——采用SISO系统的零极点匹配法。
例子
A = [0 1; -.5 -.5]
B = [1;0]
C = [1 0]
sys = ss(A,B,C)
sys_d = c2d(sys,0,1)
离散系统连续化 ¶
sysc=d2c(sysd,method)
Method:
- zoh——采用零阶保持器
- tustin——采用双线形(tustin)逼近方法
- prewarp——采用改进的tustin方法
- matched——采用SISO系统的零极点匹配法。具有接近1的极点
的情况。
注意
zoh 法不适合系统具有 z=0 的极点的情况,对于具有负实数极点的系统,该方法将增加系统的阶。 Tustin法不适合系统具有z=1
系统组合 ¶
SYS = APPEND(SYS1,SYS2, ...)
串联 ¶

sys=series(sys1,sys2)
sys=series(sys1,sys2,outputs1,inputs2)
并联 ¶

sys=parallel(sys1,sys2)
sys=parallel(sys1,sys2,inp1,inp2,out1,out2)
反馈 ¶
sys=feedback(sys1,sys2)
返回 sys1 和 sys2 的反馈连接系统 sys,反馈为负反馈。两个子系统必须连续时间系统或者具有相同采样周期的离散时间系统。
sys=feedback(sys1,sys2,sign)
sys=feedback(sys1,sys2,feedin,feedout,sign)
feedout连接到sys2的输入,sys2的输出连接到sys1的指定输入feedin,以此构成闭环
系统
框图连接 ¶
sysc=connect(sys,Q,inputs,outputs)——框图建模,sys 为由 append 生成的无连接对角方块系统,Q 矩阵用于指定系统 sys 的内部连接关系,其中矩阵的每一行对应一个输入,其第一个元素为输入编号,其后为连接该输入的输出编号,如采用负连接,则以负值表示。inputs 和 outputs 用于指定无连接系统中的某些输入 / 输出保留作为外部的输入输出
Time Domain¶
求解方程 ¶
p = pole(sys) % 求极点
z = zeros(sys) % 求零点
r = roots([1,2,3]) % 中间是多项式的参数
阶跃响应绘制 ¶
在 MATLAB 中,可以使用step函数来绘制系统的阶跃响应曲线。step函数的基本语法如下:
step(sys)
此外,还可以使用以下语法来获取阶跃响应的输出值和时间向量:
[y, t] = step(sys)
其中,y是阶跃响应的输出值向量,t是对应的时间向量。
| 求解时域指标 | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | |
S domain¶
图像绘制 ¶
pzmap(sys) % 绘制极点、零点图像
[P, Z] = pzmap(SYS)
绘制根轨迹rlocus ¶
rlocus(sys)
rlocus(SYS)
计算并绘制系统的根轨迹图。根轨迹图用来分析 负反馈系统,并显示当反馈增益从0变化到\(\infty\)时,闭环极点的轨迹。
[R, K] = RLOCUS(SYS),R=rlocus(SYS,K)
num = [1];
den = [1, 2, 1];
rlocus(num, den);
zeta = ;
sgrid(zeta,[]) % 绘制根轨迹图上的阻尼比线
min_zeta = inf; % 初始化最小阻尼比
min_zeta_pole = []; % 保存最小阻尼比对应的极点
min_zeta_K = []; % 保存最小阻尼比对应的增益
% 遍历每个增益的闭环极点,计算阻尼比
for i = 1:size(r,2)
poles = r(:,i); % 第 i 列对应的是增益 K(i) 下的闭环极点
for j = 1:length(poles)
zeta = -real(poles(j)) / abs(poles(j)); % 计算每个极点的阻尼比
if zeta < min_zeta
min_zeta = zeta; % 更新最小阻尼比
min_zeta_pole = poles(j); % 保存对应的极点
min_zeta_K = k(i); % 保存对应的增益 K
end
end
end
% 显示最小阻尼比、对应极点和增益 K
disp(['最小阻尼比: ', num2str(min_zeta)])
disp(['对应极点: ', num2str(min_zeta_pole)])
disp(['对应增益 K: ', num2str(min_zeta_K)])
根轨迹分析 ¶
rlocfind 计算给定一组根的根轨迹增益
[K, POLES] = rlocfind(SYS)
[K, POLES] = rlocfind(SYS,P)
sgrid 在连续系统根轨迹图和零极点图中绘出阻尼系数和自然频率栅格
sgrid——在连续系统的根轨迹或零极点图上绘制出栅格线,栅格线由等阻尼系数和等自然频率线构成,阻尼系数以步长 0.1 从 ξ=0 到 ξ=1 绘出
sgrid(‘new’)——先清除图形屏幕,然后绘制出栅格线,并设置成hold on,使后续绘图命令能绘制在栅格上。
sgrid(z, wn)——可制定阻尼系数 z 和自然频率 \(\omega_n\)
sgrid(‘new’, z, wn)——可制定阻尼系数 z 和自然频率 \(\omega_n\),并且在绘制栅格线之前清除图形窗口。
SISOTOOL¶
除了使用rlocus函数外,你还可以使用 MATLAB 的 SISOTOOL(单输入单输出工具)进行根轨迹设计。SISOTOOL 提供了一个交互式的界面,使你可以方便地绘制和分析根轨迹,以及设计控制器。要使用 SISOTOOL,只需在 MATLAB 命令窗口中输入sisotool即可。
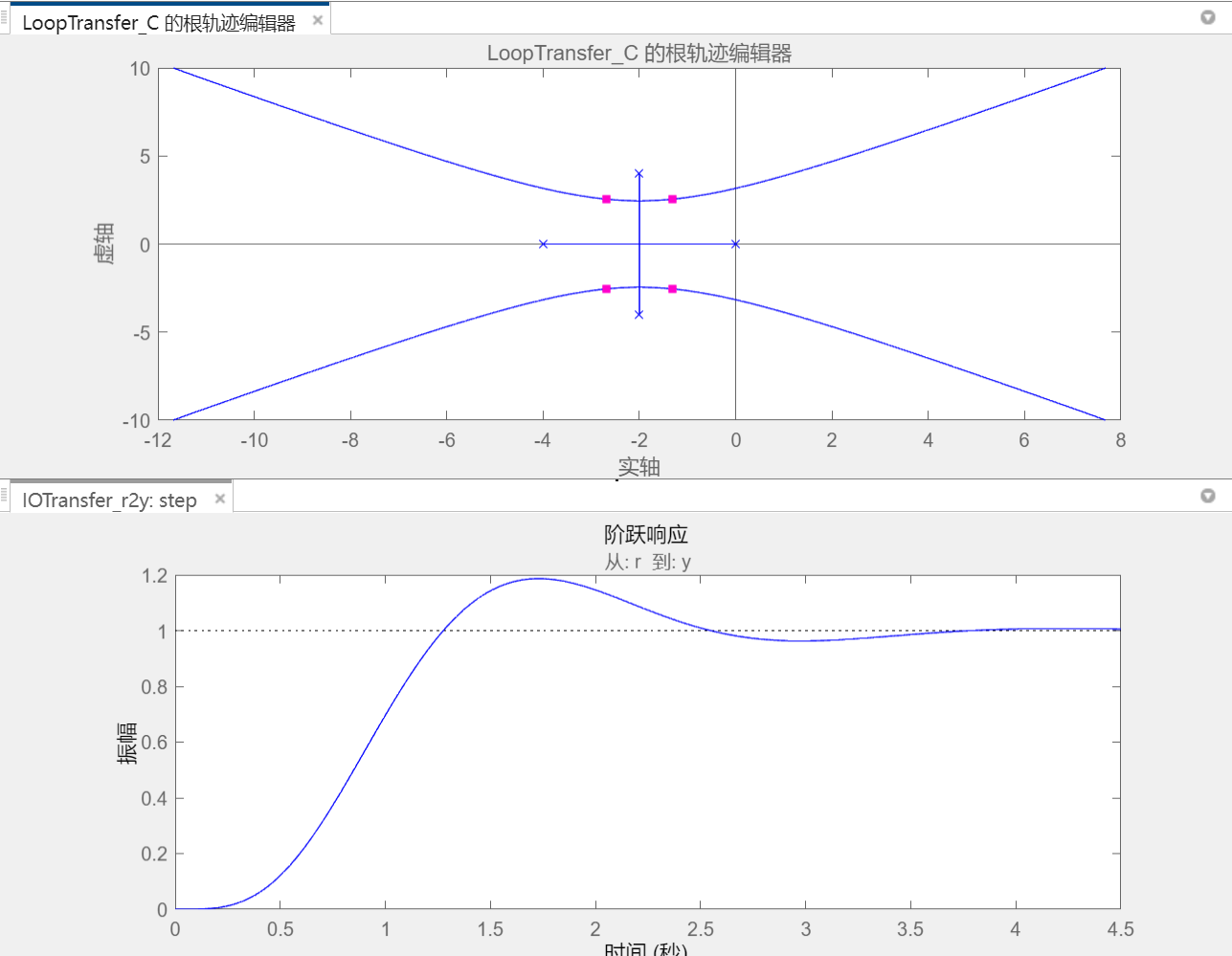
分析根轨迹 ¶
- 添加零点、极点、积分器
- 去除零点、极点、积分器
- 移动零极点
- 添加
requirement

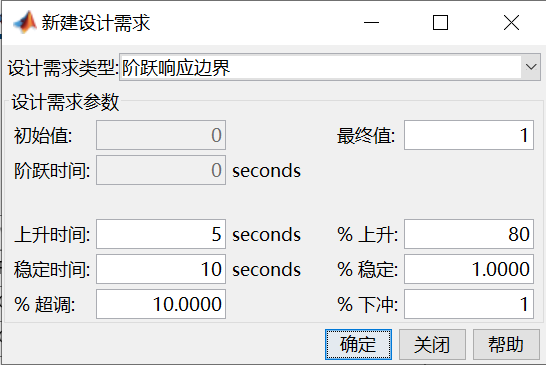
- 查看阶跃图像特征点

现代控制 ¶
能控性 ¶
Co = ctrb(A,B) # return the controllability matrix
MPC toolbox¶
基本使用 ¶
【模型预测控制】Matlab 自带 MPC Designer 工具
使用步骤 ¶
- 安装 MPC Designer
- 放一个 simulink 模型
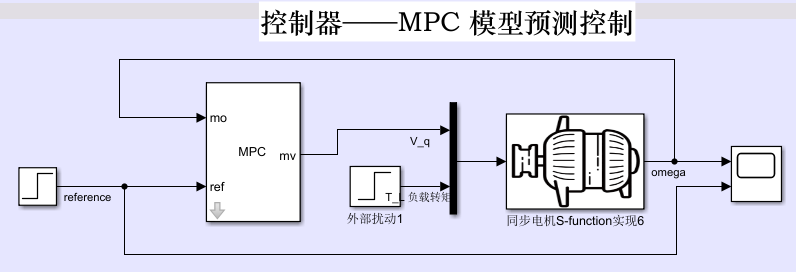
- 打开设计界面,点击 MPC Structure,设置输入输出通道,打开 I/O Attributes,设置输入输出名称
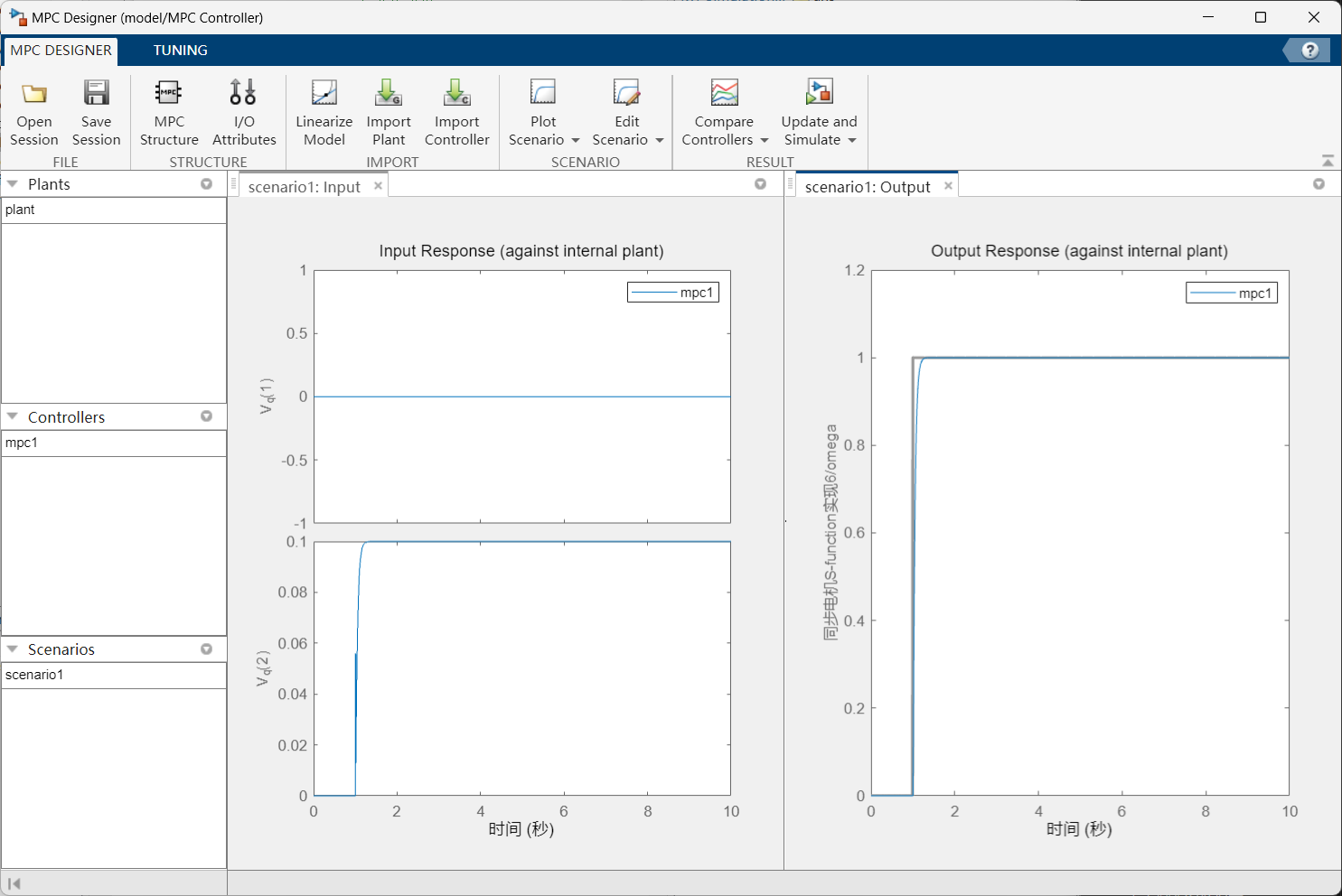
- 点击 Update and Simulate
fuzzy 工具箱 ¶
神经网络工具箱 ¶
训练 ¶
nftool
- 选择导入数据集
- 正确选择是行还是列
- 选择训练集的比例;隐藏层的个数(5or10)
- 选择训练方法:一般选择第一个方法;第二个方法和遗传算法一起用;第三个方法比较慢
validation test
validation test 表示的是泛化性能,如果连续 6 个 epoch 都上不去,就停止训练
图像查看:一般看回归的图(第四个
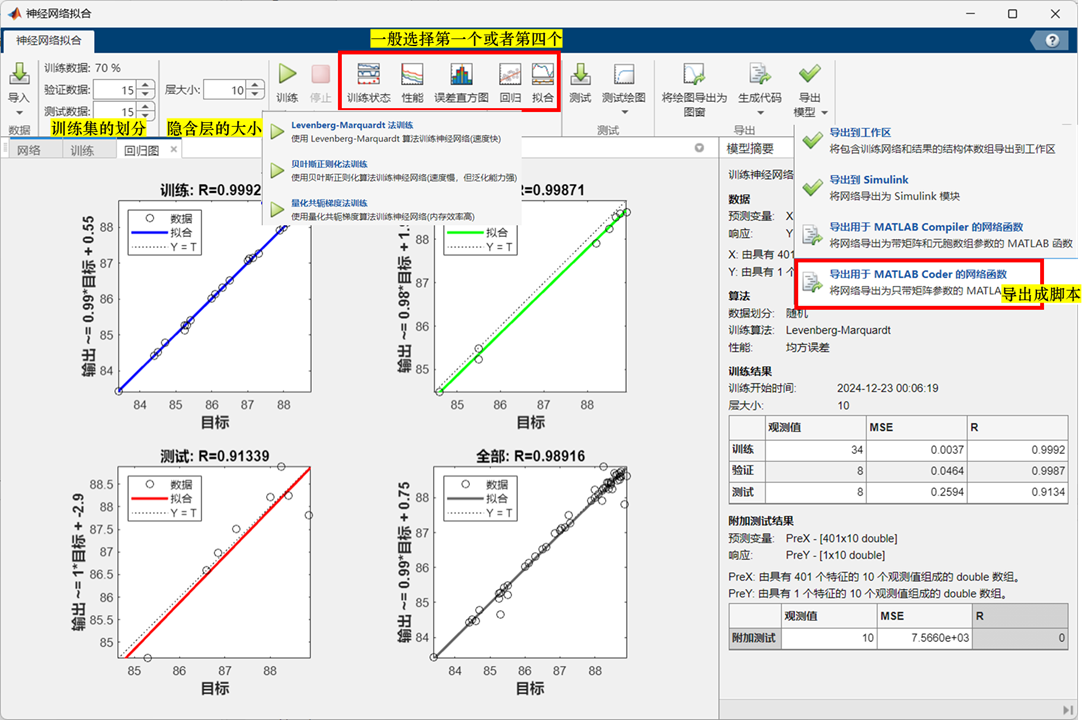
模型保存 ¶
save('filename.mat') % 保存所有变量
save('filename.mat', 'var1', 'var2') % 只保存指定变量
load('data.mat');
模型预测 ¶
PreY = zeros(10,1);
for i = 1:10
PreY(i,1) = sim(net,PreX(i,:)');
% sim函数第二个参数列数等于输入向量的个数
end
disp(PreY);
myNeuralNetworkFunction(X) % 这里需要把后两个参数去掉
多输入多输出 ¶
多输入多输出也是一样的操作,唯一值得注意的地方就是在训练之前需要将行还是列选择正确(特征 or 样本)
使用脚本替代 ui 操作 ¶
function train()
dataFile = 'data.mat';
load(dataFile); % 从文件导入数据
x = features'; % 转置为符合网络输入格式
t = labels'; % 转置为符合网络目标格式
% 选择训练函数
trainFcn = 'trainlm'; % Levenberg-Marquardt 反向传播
% 创建拟合网络
hiddenLayerSize = 15;
net = fitnet(hiddenLayerSize, trainFcn);
% 输入输出的预处理函数
net.input.processFcns = {'removeconstantrows', 'mapminmax'};
net.output.processFcns = {'removeconstantrows', 'mapminmax'};
% 设置数据的划分方式
net.divideFcn = 'dividerand'; % 随机划分数据
net.divideMode = 'sample'; % 划分所有样本
net.divideParam.trainRatio = 70/100;
net.divideParam.valRatio = 15/100;
net.divideParam.testRatio = 15/100;
% 选择性能函数
net.performFcn = 'mse'; % 均方误差
% 选择绘图函数
net.plotFcns = {'plotperform', 'plottrainstate', 'ploterrhist', ...
'plotregression', 'plotfit'};
% 训练网络
[net, tr] = train(net, x, t);
% 测试网络
y = net(x);
e = gsubtract(t, y);
performance = perform(net, t, y);
% 重新计算训练、验证和测试性能
trainTargets = t .* tr.trainMask{1};
valTargets = t .* tr.valMask{1};
testTargets = t .* tr.testMask{1};
trainPerformance = perform(net, trainTargets, y);
valPerformance = perform(net, valTargets, y);
testPerformance = perform(net, testTargets, y);
figure, plotperform(tr);% 绘制并保存训练性能图
% figure, plottrainstate(tr);% 绘制并保存训练状态图
% figure, ploterrhist(e);% 绘制并保存误差直方图
figure, plotregression(t, y)
% figure, plotfit(net, x, t);% 绘制并保存拟合图
% 保存模型
% modelFile = ['model_level' num2str(level) '.mat'];
% save(modelFile, 'net'); % 保存神经网络模型
% 生成simulink模型
gensim(net);
disp(['Model saved as ' modelFile]);
end
使用 python 训练的模型进行训练 ¶
首先下载 Deep Learning Toolbox Converter for ONNX Model Format
- 使用 pytorch 训练之后,导出 onnx 模型
- 在 matlab 中使用 onnxmodelpredict 函数进行预测(验证可行性)
model = importONNXNetwork('model.onnx', ...
'OutputLayerType', 'regression', ...
'InputDataFormats', 'BC'); % B=batch size, C=channels
% 我训练的模型输入8维,输出2维
u = [1.1; 1.1; 1.1; 1.1; 2.2; 2.2; 2.2; 2.2];
u = reshape(u, [1, 8]); % 将输入调整为 [1, 8]
y = predict(model, u);
disp('预测输出:');
disp(y);
- 在 simulink 中使用 matlab function 进行预测
Class mismatch for variable '<output of predict>'. Expected 'double', Actual 'single'.
需要强制类型转换一下
y_single = predict(model, u); % 返回的预测结果是 single 类型
y = double(y_single); % 将结果转换为 double 类型
MATLAB Function ‘xxx‘ not supported for code generation.
simlink 里面 MATLAB Function 'xxx' not supported for code generation._simulink 函数输出中不能为 mxarray-CSDN 博客 simulink代码生成的过程中,有些函数是不支持内部代码生成的,需要将其定义为外部函数,使用coder.extrinsic声明一下即可,详细的你可以参考一下matlab的帮助文档doc coder.extrinsic外部函数
coder.extrinsic('name_of_the_function');
防止重复导入模型的方法
为了防止 matlab function 每次调用的时候就导入一遍模型,使用persistent关键字声明模型
这样的话时间大大加快
function y = predictWithONNX(u)
persistent model;
coder.extrinsic('importONNXNetwork'); % 声明外部函数
if isempty(model)
% 仅当模型未加载时加载 ONNX 模型,防止重复加载消耗时间
model = importONNXNetwork('model_level2.onnx', ...
'OutputLayerType', 'regression', ...
'InputDataFormats', 'BC'); % B=batch size, C=channels
end
y = zeros(1, 2); % 初始化输出并调整输入格式
u = reshape(u, [1, 8]); % 确保输入尺寸匹配
coder.extrinsic('predict');
y_single = predict(model, u); % 返回的预测结果是 single 类型
y = double(y_single); % 将结果转换为 double 类型
end
图像绘制 ¶
绘制相平面图像 MathWorks-Teaching-Resources/Phase-Plane-and-Slope-Field: Apps for qualitative ODE analysis.
图像保存 ¶
imwrite(img,'result.jpg');
```matlab " 按照窗口进行保存 " saveas(gcf, 'save.jpg'); %保存当前窗口的图像 saveas(2, 'save.jpg'); %保存Figure 2窗口的图像
```matlab title="显示图像并保存"
x=-pi: 2*pi/ 1000:pi;
y= cos( x);
plot( x, y); print(gcf, '-djpeg', 'abc.jpg') %绘制图像并保存为jpg格式
x=-pi: 2*pi/ 1000:pi;
set(figure( 1), 'visible', 'off');
plot( x, sin( x)); print(gcf, '-dpng', 'abc.png') %不显示图像直接保存为png格式
3D animation¶
Simulink 学习——弹球仿真三维动画模型(Simulink3D 演示动画学习 01)_simulink 弹球仿真 -CSDN 博客
【免费】Bouncingball3D.slx_simulink3dsink 资源 -CSDN 文库
Simulink 3D Animation 的使用(V_realm builder2.0)-CSDN 博客
小白学习 simulink 建模开发,看这篇就够了,从入门到能够搭建完整的系统模型 _simulink 里面 vr 虚拟模型建模 -CSDN 博客
