09 | 实验 —— 机械臂仿真与实验 ¶

约 3715 个字 239 行代码预计阅读时间 17 分钟

实验要求 ¶

地点：石虎山基地时间：春 4- 春 7 周

课程安排

第一周：仿真 - 机械臂正逆运动学求解
第二周：仿真 - 机械臂轨迹规划
第三周：实物 - 机械臂抓取与放置实验

实验器材

ZJU-I 型桌面机械臂
机器人关节模组
CoppeliaSim
Python、Matlab

Coppeliasim¶

环境配置 ¶

打开文件

Windows:C:\Users\<username>\AppData\Roaming\CoppeliaSim\usrset.txt
MacOS:/Users/<username>/.CoppeliaSim/usrset.txt

将default Python项修改为所安装 Python 的路径（确保与 1 中的 python 一致）注：“\”为注释，请在其之前输入路径

找 python 路径的方法 Python: python的安装路径\python.exe Anaconda: anaconda的安装路径\envs\env_name\python.exe

创建 CoppeliaSim 的 Python 环境

conda create -n robot python=3.10
conda activate robot

查询 python 位置
which python

install python packages

pip install pyzmq
pip install cbor

仿真环境验证

完成上述仿真环境配置后，进入 Coppeliasim 软件，右键new scene中的Floor，选择Add -> Associated child script -> Non Threaded -> Python

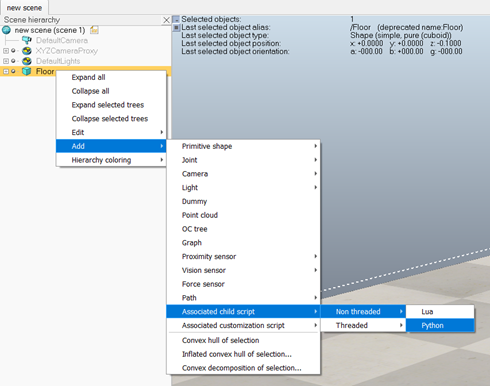
函数sysCall_init()中键入代码

floor = sim.getObject(".") # 获取当前场景中的 . 对象，"." 代表的是 当前对象，如果是在主脚本里运行，通常指的是整个场景的地面 (floor)
print(sim.getObjectPosition(floor, -1)) # 获取 floor 相对于 世界坐标系（-1 代表世界坐标系）的位置信息，返回的是 [x, y, z] 坐标。

运行并得到在控制台得到结果

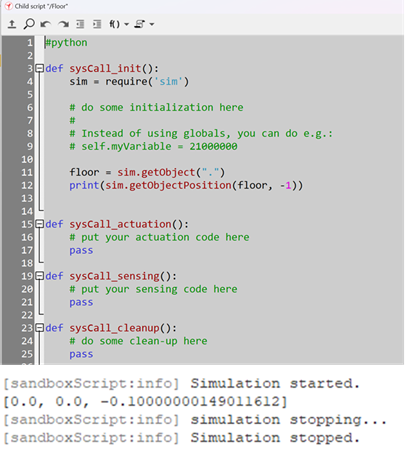
为什么 Z 轴值是 -0.1？在 CoppeliaSim 里，默认地面 (Floor) 通常不是在 z = 0，而是位于 z = -0.1。这可能是为了避免浮动误差或保证物体接触地面时的稳定性。

如果你想让地面在 z = 0，可以手动修改地面的 Z 轴位置，例如：

sim.setObjectPosition(floor, -1, [0, 0, 0])

快捷键 ¶

CTRL+<space>：开始 / 停止模拟
CTRL+E：在 1）普通，2）对象平移和 3）对象旋转鼠标模式之间切换
CTRL+D：打开对象属性对话框
CTRL+G：打开计算模块对话框
CTRL+B：调整视图以适合选定的对象；如果未选择任何对象，则调整整个场景。重点需要放在视图上。
CTRL+ALT+C：将焦点放在 Lua 命令行控制栏上
CTRL+L：清除状态栏（当焦点在 Lua 命令行控制栏上时）

代码框架入门 - 例程讲解 ¶

代码框架 ¶

双击 icon 可以打开代码

仿真中单位为米

Robot 中SuctionCup_end点展示的为机械臂末端的坐标点（仿真中为 Dummy），通过选中坐标点可以在左上角查看位姿信息（其中角度为欧拉角X-Y’-Z’）。PS：调用 API 得到的姿态信息为四元数，请注意转换。
Platform1为搬运起点的平台，其中四个物块的SuckPoint为吸盘的吸附中心点；Platform2为搬运终点的平台，其中PlacePoint为物块放置中心点；Pond为染色池，Start和End分别为起点和终点位置。PS：以上均只对位置进行了规定，但由于误差的存在，建议在规划时留一定的余量。
吸盘的吸附条件：吸盘与吸附中心点的 Z 轴夹角应小于 \(5^{\circ}\)，吸附位置应在吸附中心点为圆心、半径为 0.02m 的圆内，吸盘离物体的距离不能超过 0.005m。
在运行过程中、暂停时可以读取机械臂位置、速度、加速度和吸盘开关的状态，如下图所示。PS：停止会直接关闭。

图片来源于实验要求

Robot/Script.py¶

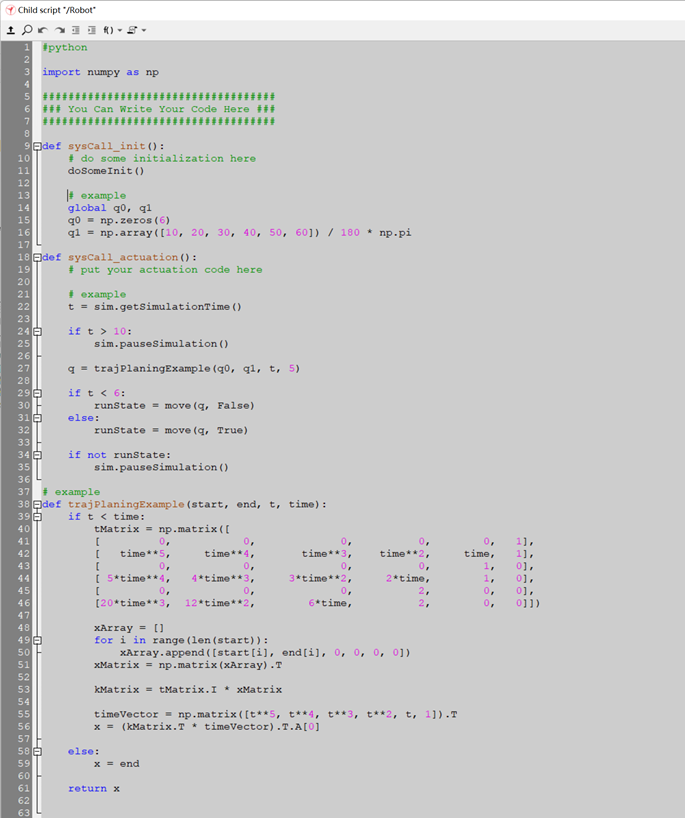
sysCall_init() 完成各关节角的计算
sysCall_actuation()中将规划好的关节角通过move(q, state)函数传输给机械臂。
move(q, state)：
- q: 机械臂各关节角度，数据类型6*1 ndarray，单位 rad；
- state，吸盘开关，数据类型bool。
- 返回值：运行成功与否，数据类型bool。

例程，拿起一个物块，停一下再扔掉

if t < 5.2:
    q = trajPlaningDemo(self.q0, self.q1, t, 5) # return the joint angles at time t
    state = False # vacumm gripper is off
    
# vacumm gripper takes effect from t=5.2s to 5.5s    
elif t < 5.5:
    q = self.q1      # keeps the robot still at q1
    state = True  # vacumm gripper is on

# lift a block and move to q2    
elif t < 8.7:
    q = trajPlaningDemo(self.q1, self.q2, t-5.5, 3)
    state = True

# release the vaccum gripper
elif t < 9:
    q = self.q2 
    state = False
else:
    # robot moves from q2 to q0 within 5s
    q = trajPlaningDemo(self.q2, self.q0, t-9, 5)
    state = False

时间 ( 秒 )	任务描述	夹持器状态
0 - 5.2	机器人从 `q0` 移动到 `q1`	❌ 关闭
5.2 - 5.5	机器人停留在 `q1`，夹持器启动	✅ 开启
5.5 - 8.7	机器人从 `q1` 移动到 `q2`（搬运物体）	✅ 开启
8.7 - 9	机器人停在 `q2`，夹持器关闭（释放物体）	❌ 关闭
9 - 14	机器人从 `q2` 移动回 `q0`	❌ 关闭
> 20	停止仿真	❌ 关闭

问题与解决 ¶

Traceback (most recent call last): UnicodeDecodeError: 'utf-8' codec can't decode byte 0xbb in position 27: invalid start byte

检查路径中是否有中文地址，改成英文

AttributeError: module 'IK' has no attribute 'IKSolver'

在.py文件的开头，修改正确的 IK 文件夹的位置

仿真实验 1：机械臂正、逆运动学求解 ¶

机械臂几何参数 ¶

每一轴的位置、速度、加速度约束（当前状态是各个关节零点）

	关节一	关节二	关节三	关节四	关节五	关节六
最小关节值	\(-200^\circ\)	\(-90^\circ\)	\(-120^\circ\)	\(-150^\circ\)	\(-150^\circ\)	\(-180^\circ\)
最大关节值	\(200^\circ\)	\(90^\circ\)	\(120^\circ\)	\(150^\circ\)	\(150^\circ\)	\(180^\circ\)

	关节一	关节二	关节三	关节四	关节五	关节六
关节速度	\(100^\circ/s\)	\(100^\circ/s\)	\(100^\circ/s\)	\(100^\circ/s\)	\(100^\circ/s\)	\(100^\circ/s\)
关节加速度	\(500^\circ/s^2\)	\(500^\circ/s^2\)	\(500^\circ/s^2\)	\(500^\circ/s^2\)	\(500^\circ/s^2\)	\(500^\circ/s^2\)

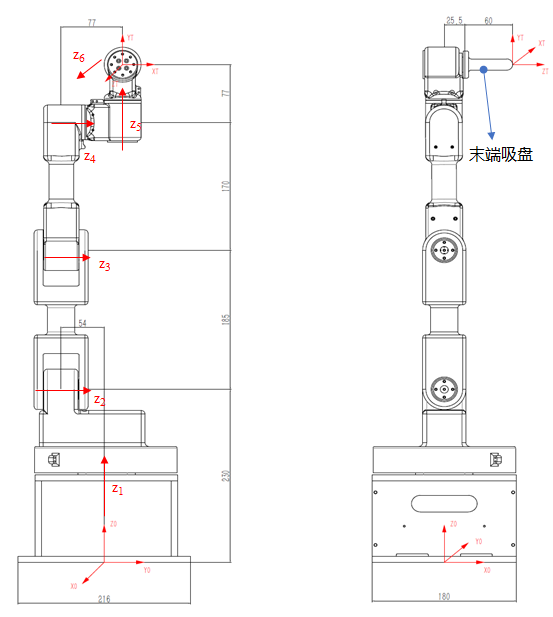
图源课程实验要求

实验要求 ¶

写出 ZJU-I 型桌面机械臂的 DH 参数；
写出 ZJU-I 型机械臂的正运动学解（不用给出最终的齐次变换矩阵的具体代数式），并采用 \(XY'Z'\) 欧拉角表示末端执行器姿态；
将以下 5 组关节角参数带入正运动学解，计算机械臂末端 Tip 点的空间位置，计算末端执行器的姿态，以 \(XY'Z'\) 欧拉角表示结果，写出计算过程；
- 第一组：\(\left(\frac{\pi}{6}, 0,\frac{\pi}{6}, 0, \frac{\pi}{3}, 0\right)\)
- 第二组：\(\left(\frac{\pi}{6}, \frac{\pi}{6}, \frac{\pi}{3}, 0,\frac{\pi}{3}, \frac{\pi}{6}\right)\)
- 第三组：\(\left(\frac{\pi}{2}, 0, \frac{\pi}{2}, -\frac{\pi}{3}, \frac{\pi}{3}, \frac{\pi}{6}\right)\)
- 第四组：\(\left(-\frac{\pi}{6}, -\frac{\pi}{6}, -\frac{\pi}{3}, 0, \frac{\pi}{12}, \frac{\pi}{2}\right)\)
- 第五组：\(\left(\frac{\pi}{12}, \frac{\pi}{12}, \frac{\pi}{12}, \frac{\pi}{12}, \frac{\pi}{12}, \frac{\pi}{12}\right)\)
将以上 5 组关节角分别输入仿真程序，将仿真得到的末端位姿与第 3 步得到的计算结果进行比对。
写出 ZJU-I 型桌面机械臂的逆运动学解析解（可选）；
将如下 5 组末端位姿参数分别代入逆运动学解（可使用自带的逆运动学求解器进行相关计算），计算对应的 5 组关节角；
- 第一组：\((0.117,0.334,0.499,-2.019,-0.058, -2.190)\)
- 第二组：\((-0.066, 0.339, 0.444, -2.618, -0.524, -3.141)\)
- 第三组：\((0.3, 0.25, 0.26, -2.64, 0.59, -2.35)\)
- 第四组：\((0.42, 0, 0.36, 3.14, 1, -1.57)\)
- 第五组：\((0.32, -0.25, 0.16, 3, 0.265, -0.84)\)
将所求关节角作为参数输入仿真程序，从仿真中得到机械臂末端执行器的空间位置和姿态，与第 6 步给定的位置和姿态进行比对。

报告要求

机械臂正、逆运动学求解 1）ZJU-I型机械臂的DH参数
2）机械臂的正运动学及其仿真结果
3）机械臂的逆运动学及其仿真结果

最终提交文件，需包括

1）组号 - 实验报告.docx/pdf（推荐 pdf） 2）组号-代码文件.rar/zip：Coppeliasim仿真软件的.ttt文件及包含的其他代码文件 3）组号-仿真结果.mp4/mov/其他视频文件格式：机械臂轨迹规划仿真实验的录屏文件（文件大小应小于50Mb，推荐使用Win+G中的“捕获”进行录制）

DH 参数 ¶

	\(\alpha\)	\(a\)	\(d\)	\(\theta\)
1	0	0	0.23	\(\theta_1\)
2	\(-\pi/2\)	0	-0.054	\(\theta_2-\pi/2\)
3	0	0.185	0	\(\theta_3\)
4	0	0.170	0.077	\(\theta_4+\pi/2\)
5	\(\pi/2\)	0	0.077	\(\theta_5+\pi/2\)
6	\(\pi/2\)	0	0.0855	\(\theta_6\)

正运动学 ¶

任务在要求干什么

在仿真软件中，输入要求的关节角，从起始位置运动到这个要求的位置
通过手算 /matlab/python，计算出末端执行器最后的变换矩阵
将计算出的末端执行器的位置和姿态与仿真软件中的结果进行比对

仿真软件执行

仿真软件当中执行的代码
def sysCall_actuation():
    q0 = np.zeros(6) # initialize q0 with all zeros
    q1 = np.array([np.pi/6, 0, np.pi/6, 0, np.pi/3, 0])
    q2 = np.array([np.pi/6, np.pi/6, np.pi/3, 0, np.pi/3, np.pi/6])
    q3 = np.array([np.pi/2, 0, np.pi/2, -np.pi/3, np.pi/3, np.pi/6])
    q4 = np.array([-np.pi/6, -np.pi/6, -np.pi/3, 0, np.pi/12, np.pi/2])
    q5 = np.array([np.pi/12, np.pi/12, np.pi/12, np.pi/12, np.pi/12, np.pi/12])

    t = sim.getSimulationTime()
    q = trajPlaningDemo(q0, q1, t, 2) # 修改这里改成不同的点
    print(sim.getObjectPosition(sim.getObject('/Robot/SuctionCup/SuctionCup_end'))+sim.getObjectOrientation(sim.getObject('/Robot/SuctionCup/SuctionCup_end'))) # 输出位置信息
    a = move(q,0)

解算变换矩阵，计算末端参数

需要特别注意的点：

注意 DH 参数表当中的单位，图片中的单位是毫米，软件当中是米
注意 \(\theta\) 的初始值，需要保证 \(\theta_i = 0\) 时候，机械臂初始位姿正确 (\(\pm\frac{\pi}{2}\) 的原因 )
需要特别注意最后的欧拉角表示是 XYZ 表示方法，所以由旋转矩阵计算欧拉角的时候需要注意更换一下公式；

使用 Matlab 计算变换矩阵
calculate_XYZ_euler_angles([pi/6, 0, pi/6, 0, pi/3, 0],1);
calculate_XYZ_euler_angles([pi/6, pi/6, pi/3, 0, pi/3, pi/6],2);
calculate_XYZ_euler_angles([pi/2, 0, pi/2, -pi/3, pi/3, pi/6],3);
calculate_XYZ_euler_angles([-pi/6, -pi/6, -pi/3, 0, pi/12, pi/2],4);
calculate_XYZ_euler_angles([pi/12, pi/12, pi/12, pi/12, pi/12, pi/12],5);


function calculate_XYZ_euler_angles(theta_values,i)
    fprintf("%d",i);
    % 基础DH参数表
    DH_params_base = [
        0, 0, 0.23, 0;
        -pi/2, 0, -0.054, -pi/2;
        0, 0.185, 0, 0;
        0, 0.170, 0.077, pi/2;
        pi/2, 0, 0.077, pi/2;
        pi/2, 0, 0.0855, 0
    ];

    % 创建完整的DH参数表
    DH_params = DH_params_base;
    for i = 1:length(theta_values)
        DH_params(i, 4) = theta_values(i) + DH_params_base(i, 4);  % 添加theta值
    end

    % 计算最终变换矩阵
    T_final = compute_DH(DH_params);
    fprintf('Position\n');
    disp(T_final(1:3,4));
    
    % 需要特别注意这里是XYZ方法
    R = T_final(1:3, 1:3);

    beta_calc = asin( R(1, 3));
    alpha_calc = atan2(-R(2, 3), R(3, 3));
    gamma_calc = atan2(-R(1, 2), R(1, 1));

    euler_angles_deg = rad2deg([alpha_calc, beta_calc, gamma_calc]); % 转换为弧度
    fprintf('Angle\n');
    disp(euler_angles_deg);
end

计算变换矩阵
function T_final = compute_DH(DH_params)
    n = size(DH_params, 1);  % Number of joints
    T_final = eye(4);
  
    for i = 1:n
        theta_i = DH_params(i, 4);
        d_i = DH_params(i, 3);
        a_i_minus_1 = DH_params(i, 2);
        alpha_i_minus_1 = DH_params(i, 1);
      
        % 计算每个关节的变换矩阵 MDH方法
        T_i = [
            cos(theta_i), -sin(theta_i), 0, a_i_minus_1;
            sin(theta_i) * cos(alpha_i_minus_1), cos(theta_i) * cos(alpha_i_minus_1), -sin(alpha_i_minus_1), -sin(alpha_i_minus_1) * d_i;
            sin(theta_i) * sin(alpha_i_minus_1), cos(theta_i) * sin(alpha_i_minus_1), cos(alpha_i_minus_1), cos(alpha_i_minus_1) * d_i;
            0, 0, 0, 1
        ];
      
        T_final = T_final * T_i;
    end
  
    % 打印最终变换矩阵
    fprintf('Final Transformation Matrix T = \n');
    disp(T_final);
end

对比得到结果

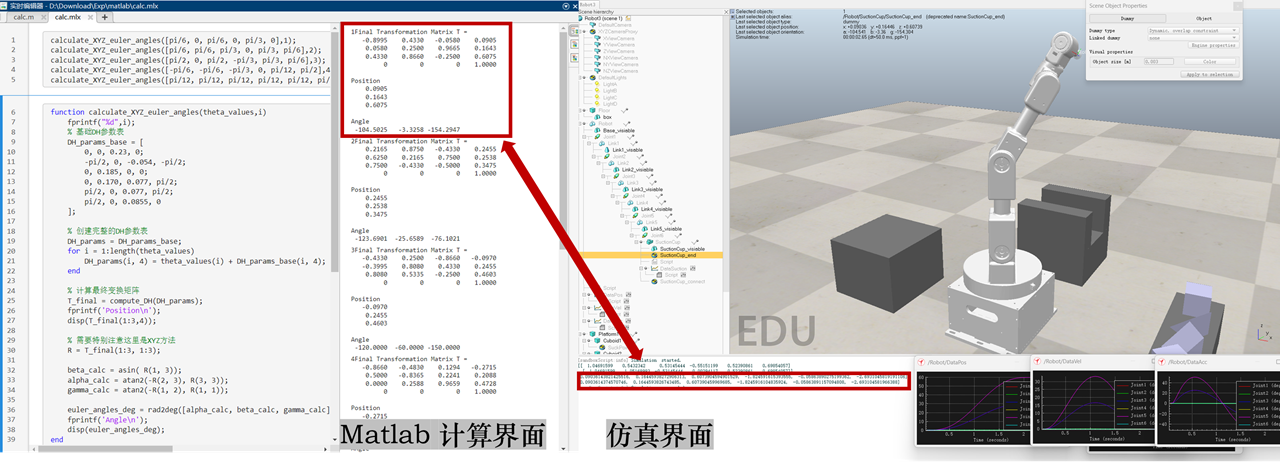
逆运动学 ¶

这里使用IK库即可求解基础解

但是需要注意的是，关节角度有限制，所以需要将不符合关节角度限制的解去除。这里使用了np.all函数加上逻辑表达式进行判断，简化了逻辑判断

步骤：

使用逆运动学求解器得到解（可能有多个，按照要求选择一个）
将解带入正运动学
观察末端坐标和原先给定坐标是否一致

逆运动学求解与验证
def sysCall_init():
    sim = require('sim')
    # initialization the simulation
    doSomeInit()    # must have   

    angles_array = np.array([
        [0.117, 0.334, 0.499, -2.019, -0.058, -2.190],
        [-0.066, 0.339, 0.444, -2.618, -0.524, -3.141],
        [0.3, 0.25, 0.26, -2.64, 0.59, -2.35],
        [0.42, 0, 0.36, 3.14, 1, -1.57],
        [0.32, -0.25, 0.16, 3, 0.265, -0.84]
    ])
    
    iks = IK.IKSolver()
    i = 2 # 手动从0-4
    angles = iks.solve(angles_array[i])
    
    min_vals = np.radians([-200, -90, -120, -150, -150, -180])
    max_vals = np.radians([200, 90, 120, 150, 150, 180])

    valid_columns = ((min_vals[:, None] <= angles) & (angles <= max_vals[:, None])).all(axis=0) # 验证是否在范围内
    valid_angles = angles[:, valid_columns].transpose() # 把符合条件的列提取出来
    print(valid_angles)
    global test_example
    test_example = valid_angles[0] # 从符合的样例当中抽选一个
    
    
def sysCall_actuation():
    t = sim.getSimulationTime()
    q = trajPlaningDemo(q0, test_example, t, 2)
    a = move(q,0)
    if(t>2.5):
        print(sim.getObjectPosition(sim.getObject('/Robot/SuctionCup/SuctionCup_end'))+sim.getObjectOrientation(sim.getObject('/Robot/SuctionCup/SuctionCup_end')))
        sim.pauseSimulation() # 暂停,也可以使用stopSimulation()

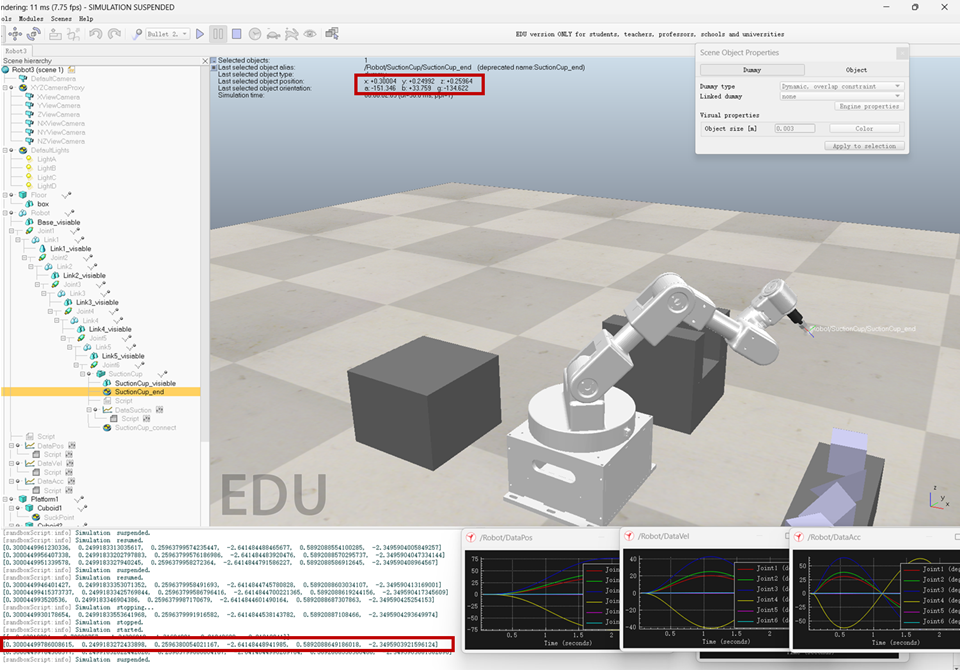
可以看到红框的部分是一致的，可以验证了逆运动学的正确性

仿真实验 2 ：机械臂点到点轨迹规划 ¶

通过控制机械臂关节运动，将机械臂末端执行器从起点在规定时间内运动到终点

注意各个关节轴的位置、速度、加速度限制，若超出限制将会停止运行！！！

不限制规划方案，但是需要注意，最终的成绩与机械臂运行合理性、关节轴速度和加速度连续性等相关。

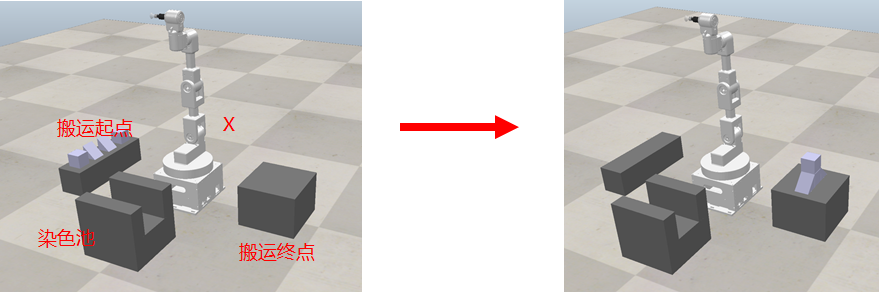
要求：

起点位姿 \((0.117,0.334,0.499,-2.019,-0.058,-2.190)\)
终点位姿 \((0.32,-0.25,0.16,3,0.265,-0.84)\)
初始速度：0；终点速度：0；运行时间：2 秒

报告要求

机械臂轨迹规划，具体需包括

1）仿真实验整体方案介绍
2）机械臂的轨迹规划方案
3）轨迹规划仿真结果（视频）

最终提交文件，需包括

1）组号 - 实验报告.docx/pdf（推荐 pdf）
2）组号-代码文件.rar/zip：Coppeliasim仿真软件的.ttt文件及包含的其他代码文件
3）组号-仿真结果.mp4/mov/其他视频文件格式：机械臂轨迹规划仿真实验的录屏文件（文件大小应小于50Mb，推荐使用Win+G中的“捕获”进行录制）

实物实验 1：六自由度机械臂物体抓取与放置实验 ¶

编写程序控制 ZJU-I 型机械臂，实现木块抓取与搬运，具体流程为：
- 机械臂从零位置启动，运行至起始区域；
- 启动真空吸爪，抓取起始区域内的木块，移动至 A 点 \((370,-90,115)\)；
- 移动过程中控制木块从 A 点沿直线路径运动至 B 点 \((288,-288,115)\)；
- 控制从 B 点到达目标区域，目标区域位置为机械臂 1 号关节旋转角度 \(90^\circ\) 所在位置；
- 抓取第二个木块放置到目标区域，并堆叠在第一个模块上，二者姿态保持一致；
程序中需要编写正、逆运动学求解代码、轨迹规划代码，要求机械臂无碰撞、所有关节速度平滑；
分组完成实验，每组提交一份实验报告，内容不超过 4 页；

实验解释 ¶

说人话：这个实验在干什么

需要找到一个没有坏的机械臂，很多组的都已经坏掉了
连接串口，运行老师给到的测试程序，看看能不能动
期望的现象：机械臂从起始位置运动到第一个物体，吸盘吸附物体，移动到 A 点，再直线移动到 B 点，再移动到目标区域，放下物体
B 点的操作是类似的

遇到的问题与解决方法：

连接不上机械臂： - 解决方法：检查串口是否正确，USB线是否连接好，电源是否打开；红色紧急停止按钮不要旋下去 - mac当中需要使用ls /dev/tty.*来查看串口，注意权限问题；但是老师也没有提供arm架构下的库文件，所以只有intel架构的mac才能做这个实验

例程解释 ¶

例程中主要给了两组函数，分别实现使用五次多项式规划两点之间轨迹和三点之间轨迹的规划（可以指定中间点的位置和速度）。

`quinticCurvePlanning(startPosition, endPosition, time)`¶

两点间五次多项式轨迹规划

# 返回值kArray为多项式系数
def quinticCurvePlanning(startPosition, endPosition, time):
    timeMatrix = np.matrix([
        [         0,           0,             0,          0,        0,   1],
        [   time**5,     time**4,       time**3,    time**2,     time,   1],
        [         0,           0,             0,          0,        1,   0],
        [ 5*time**4,   4*time**3,     3*time**2,     2*time,        1,   0],
        [         0,           0,             0,          2,        0,   0],
        [20*time**3,  12*time**2,        6*time,          2,        0,   0]
    ])
    invTimeMatrix = np.linalg.inv(timeMatrix)
    kArray = []
    for i in range(len(startPosition)):
        X = np.matrix([startPosition[i], endPosition[i], 0, 0, 0, 0]).T
        k = np.dot(invTimeMatrix, X)
        kArray.append(k)
    return kArray

作用: 计算两点间五次多项式轨迹的系数。
输入:
- startPosition: 起始位置数组。
- endPosition: 终止位置数组。
- time: 运动时间。
输出: 多项式系数数组 kArray。
原理: 构造时间矩阵，求逆矩阵，计算多项式系数。

`quinticCurveExcute(kArray, time)`¶

作用: 根据五次多项式系数和时间计算关节位置。
输入:
- kArray: 多项式系数数组。
- time: 当前时间。
输出: 当前关节位置数组 jointPositions。
原理: 将时间代入多项式计算关节位置。

两点间规划，求得当前时刻下的关节位置值

def quinticCurveExcute(kArray, time):
    timeVector = np.matrix([time**5,     time**4,       time**3,    time**2,     time,   1]).T
    jointPositions = []
    for i in range(6):
        jointPosition = np.dot(kArray[i].T, timeVector)
        jointPositions.append(jointPosition[0, 0])
    return np.array(jointPositions)

`quinticCurvePlanning2(...)`¶

作用: 计算三点间五次多项式轨迹的系数。
输入:
- startPosition: 起始位置数组。
- middlePosition: 中间位置数组。
- endPosition: 终止位置数组。
- midVel: 中间点速度。
- time: 起点到中间点时间。
- time1: 起点到终点时间。
输出: 多项式系数数组 kArray。
原理: 构造时间矩阵，求逆矩阵，计算多项式系数。

三点间五次多项式轨迹规划

# 返回值kArray为多项式系数，其中起点终点速度均为零，中间点速度可以规划，为入参midVel
# 其中time为起点到中间点的运动时间，time1为起始点到终点的运动时间（即整段规划的运动时间）
def quinticCurvePlanning2(startPosition, middlePosition, endPosition, midVel, time, time1):
    timeMatrix = np.matrix([
        [          0,            0,              0,           0,        0,   1],
        [    time**5,      time**4,        time**3,     time**2,     time,   1],
        [   time1**5,     time1**4,       time1**3,    time1**2,    time1,   1],
        [          0,            0,              0,           0,        1,   0],
        [  5*time**4,    4*time**3,      3*time**2,      2*time,        1,   0],
        [ 5*time1**4,   4*time1**3,     3*time1**2,     2*time1,        1,   0],
    ])
    invTimeMatrix = np.linalg.inv(timeMatrix)
    kArray = []
    for i in range(len(startPosition)):
        X = np.matrix([startPosition[i], middlePosition[i], endPosition[i], 0, midVel, 0]).T
        k = np.dot(invTimeMatrix, X)
        kArray.append(k)
    return kArray

`quinticCurveExcute2(kArray, time)`¶

三点间规划，求得当前时刻下的关节位置值

def quinticCurveExcute2(kArray, time):
    timeVector = np.matrix([time**5,     time**4,       time**3,    time**2,     time,   1]).T
    jointPositions = []
    for i in range(6):
        jointPosition = np.dot(kArray[i].T, timeVector)
        jointPositions.append(jointPosition[0, 0])
    return np.array(jointPositions)

作用: 根据三点间五次多项式系数和时间计算关节位置。
输入:
- kArray: 多项式系数数组。
- time: 当前时间。
输出: 当前关节位置数组 jointPositions。
原理: 将时间代入多项式计算关节位置。

一些需要注意的点 ¶

起始点是需要自己确定的，我自己选的是和 A 点 x 相同，y 大一些的两个点
旋转 90 度的坐标位置可以通过简单的全等三角形知识得出
需要注意坐标系当中的单位问题，之前实验中的单位是米，这里是毫米
贵重物品最好远离机械臂，避免代码中的 bug 导致机械臂突然发疯

求解代码 ¶

# from Robot.Robot import Robot
import numpy as np
import until
import time
from until import InverseKinamatics
import math

def go(r, runtime, *k_list):
    T, t, flag = 0.02, 0, 0
    r.go_home()
    while t < runtime[-1]:
        start = time.time()
        for i, k in enumerate(k_list):
            if runtime[i] <= t < runtime[i + 1]:
                if i == 1 and not flag:
                    time.sleep(2)
                    flag = 1
                if i == 3:
                    q = until.quinticCurveExcute2(k, t - runtime[i])
                else:   
                    q = until.quinticCurveExcute(k, t - runtime[i])
                break
        else:
            time.sleep(2)
            r.go_home()
            break
        r.syncMove(np.reshape(q, (6, 1)))
        t += T
        time.sleep(max(0, T - (time.time() - start)))

获取坐标点
def get_position():
    q0 = np.zeros(6)
    object_1 = InverseKinamatics(np.array([0.370,0.010,0.10, -np.pi, 0, -np.pi/2]), q0)/math.pi*180
    P_A_1 = InverseKinamatics(np.array([0.370,-0.090,0.21, -np.pi, 0, -np.pi/2]), object_1)/math.pi*180
    P_B_1 = InverseKinamatics(np.array([0.288,-0.288,0.21, -np.pi, 0, -np.pi/2]), P_A_1)/math.pi*180
    helper_1 = InverseKinamatics(np.array([0.01,-0.37,0.25, -np.pi, 0, -np.pi/2]), P_B_1)/math.pi*180
    end_1 = InverseKinamatics(np.array([0.01,-0.37,0.11, -np.pi, 0, -np.pi/2]), helper_1)/math.pi*180
    
    
    object_2 = InverseKinamatics(np.array([0.370,0.120,0.10, -np.pi, 0, -np.pi/2]), q0)/math.pi*180
    P_A_2 = InverseKinamatics(np.array([0.370,-0.090,0.21, -np.pi, 0, -np.pi/2]), object_2)/math.pi*180
    P_B_2 = InverseKinamatics(np.array([0.288,-0.288,0.21, -np.pi, 0, -np.pi/2]), P_A_2)/math.pi*180
    helper_2 = InverseKinamatics(np.array([0.01,-0.37,0.30, -np.pi, 0, -np.pi/2]), P_B_2)/math.pi*180
    end_2 = InverseKinamatics(np.array([0.01,-0.37,0.17, -np.pi, 0, -np.pi/2]), helper_2)/math.pi*180
    return q0, object_1, P_A_1, P_B_1, helper_1,end_1, object_2, P_A_2, P_B_2, helper_2,end_2

控制逻辑

def move():
    # com: Windows: "COM3" Linux: "/dev/ttyUSB0" Mac: "/dev/tty.usbserial-*"
    r = Robot(com='COM9', baud=250000)
    r.connect()

    q0, object_1, P_A_1, P_B_1, helper_1,end_1, object_2, P_A_2, P_B_2, helper_2,end_2 = get_position()
    
    t1 = [2,3,2,4]
    runtime = [sum(t1[:i+1]) for i in range(len(t1))]

    # 抓取第一个物体

    k_0 = until.quinticCurvePlanning(q0,object_1,t1[0])
    k_1 = until.quinticCurvePlanning(object_1,P_A_1,t1[1])
    k_2 = until.quinticCurvePlanning(P_A_1,P_B_1,t1[2])
    k_3 = until.quinticCurvePlanning2(P_B_1,helper_1,end_1,t1[3]*0.45,t1[3]) # 经过中间点的轨迹规划
    go(r,runtime,k_0,k_1,k_2,k_3)

    # 抓取第二个物体
    
    k_0 = until.quinticCurvePlanning(q0,object_2,t1[0])
    k_1 = until.quinticCurvePlanning(object_2,P_A_2,t1[1])
    k_2 = until.quinticCurvePlanning(P_A_2,P_B_2,t1[2])
    k_3 = until.quinticCurvePlanning2(P_B_2,helper_2,end_2,t1[3]*0.45,t1[3])
    go(r,runtime,k_0,k_1,k_2,k_3) # 经过中间点的轨迹规划

if __name__ == '__main__': 
    move()

Explore¶

Pybullet 环境配置 ¶

查看 Matlab 支持的 Python 版本

Versions of Python Compatible with MATLAB Products by Release - MATLAB & Simulink

maltab 与 pybullet 联合仿真 - _ 夜尘 - 博客园

pybullet 学习（一）——安装与入门 pybullet-CSDN 博客

PyBullet 笔记（一）pybullet 及其依赖项的安装、pybullet 初探 - 知乎

官方笔记

https://docs.google.com/document/d/10sXEhzFRSnvFcl3XxNGhnD4N2SedqwdAvK3dsihxVUA/edit?tab=t.0

openai/baselines: OpenAI Baselines: high-quality implementations of reinforcement learning algorithms

pip install pybullet

由于 pybullet 中一些开箱即用的模型是通过 tensorflow 实现的，所以 tensorflow 也需要装一下：

pip install tensorflow

pybullet 的官方也提供了一些好玩的 demo，不过这些 demo 需要额外下载，先进入 windows 下一个你想要安放这些 baselines 的目录，然后输入：

git clone https://github.com/openai/baselines.git
cd baselines
pip install -e .

09 | 实验 —— 机械臂仿真与实验 ¶

实验要求 ¶

Coppeliasim¶

环境配置 ¶

快捷键 ¶

代码框架入门 - 例程讲解 ¶

代码框架 ¶

Robot/Script.py¶

问题与解决 ¶

仿真实验 1：机械臂正、逆运动学求解 ¶

机械臂几何参数 ¶

实验要求 ¶

DH 参数 ¶

正运动学 ¶

逆运动学 ¶

仿真实验 2 ：机械臂点到点轨迹规划 ¶

实物实验 1：六自由度机械臂物体抓取与放置实验 ¶

实验解释 ¶

例程解释 ¶

quinticCurvePlanning(startPosition, endPosition, time)¶

quinticCurveExcute(kArray, time)¶

quinticCurvePlanning2(...)¶

quinticCurveExcute2(kArray, time)¶

一些需要注意的点 ¶

求解代码 ¶

Explore¶

Pybullet 环境配置 ¶

`quinticCurvePlanning(startPosition, endPosition, time)`¶

`quinticCurveExcute(kArray, time)`¶

`quinticCurvePlanning2(...)`¶

`quinticCurveExcute2(kArray, time)`¶