跳转至

05 | 轨迹规划

约 2333 个字 106 行代码 预计阅读时间 10 分钟

（Trajectory Planning） 为每个关节计算连续的运动轨迹，使末端执行器在空间中从点A移动到点B

特性 关节空间规划 笛卡尔空间规划
定义 在关节空间中规划每个关节的运动轨迹，使末端执行器达到目标位置。 在笛卡尔空间中直接规划末端执行器的运动轨迹。
优点 - 计算简单，适合大多数机器人控制器。 - 轨迹直观，便于控制末端执行器的运动路径。
缺点 - 末端执行器的路径可能不直观，可能出现不必要的绕行。 - 计算复杂，可能需要逆运动学求解，增加计算负担。
适用场景 - 对路径形状要求不高的任务，例如点到点的运动。 - 对路径形状有严格要求的任务，例如绘图或焊接。
插值方法 - 直接对关节角度进行插值。 - 需要对末端位置或姿态进行插值，可能涉及旋转矩阵或四元数的处理。
运动平滑性 - 关节运动平滑，但末端执行器路径可能不平滑。 - 末端执行器路径平滑，但可能导致关节运动不平滑。

关节空间规划

方法 平滑性 计算复杂度 加速度连续性 适用场景
线性插值 低（速度突变） 低 不连续 简单、低速
抛物线过渡 中（速度连续） 中 不连续 中等速度，允许加速度突变
分段三次多项式 高（速度 / 加速度连续） 中高 连续 平滑加减速的中高速运动
五次多项式 极高（全局连续） 高 连续 高精度、高动态性能需求

线性插值

线性插值是一种简单的轨迹规划方法，通过在起点和终点之间进行线性插值来计算中间点的位置。其公式如下：

\[ \phi(t) = \phi_0 + (\phi_f - \phi_0) \cdot \frac{t}{T} \]

其中：

  • \(\phi_0\) 为起始位置，
  • \(\phi_f\) 为终止位置，
  • \(t\) 为当前时间，
  • \(T\) 为总时间。

线性插值的优点是计算简单，适用于对路径平滑性要求不高的场景，但其缺点是速度和加速度可能会出现突变。

linear_interpolation
import numpy as np

def linear_interpolation(start, end, t, duration):
    """
    线性插值轨迹规划
    :param start: 起始点坐标
    :param end: 终点坐标
    :param t: 当前时间
    :param duration: 总时长
    :return: 当前时刻的位置
    """
    if t < duration:
        x_array = start * (1 - t / duration) + end * (t / duration)
        x_angles = inverse_kinematics(x_array)
    else:
        x_angles = inverse_kinematics(end)
    return x_angles

三次多项式：规划位置 & 速度

\[ \phi(t) = a_0 + a_1t + a_2t^2 + a_3t^3 \]

这里有四个未知数，所以需要四个约束条件，选择初始位置、初始速度、终止位置、终止速度（一般都是给定的）

用给定的数据求解方程，得到四个系数，然后就可以得到轨迹方程。

三次 + 中间点

指定中间点速度

每一段都使用三次多项式进行规划。

  • 前后两段斜率符号相同：速度取平均值
  • 前后两段斜率符号不同：速度取 0

不指定中间点速度

\[ \phi_{ij}(t) = a_0 + a_1t + a_2t^2 + a_3t^3\\ \phi_{jk}(t) = b_0 + b_1t + b_2t^2 + b_3t^3 \]

有八个未知数，所以需要八个约束条件，一种方式是

  • 位置约束：第一段起点终点，第二段起点终点
  • 速度约束：第一段起点速度，第二段终点速度，中间点速度相等
  • 加速度联系约束：中间点加速度相等
cubic_spline
def cubic_spline(start, end, t, duration):
    """
    分段三次多项式插值
    :param start: 起始点坐标
    :param end: 终点坐标
    :param t: 当前时间
    :param duration: 总时长
    :return: 当前时刻的位置
    """
    if t < duration:
        tx = t / duration
        if t < 0.25 * duration:
            tx = 32 / 6 * (tx ** 3)
        elif t < 0.5 * duration:
            tx = -32 / 6 * (tx - 0.25) ** 3 + 4 * (tx - 0.25) ** 2 + tx - 0.25 + 1 / 12
        elif t < 0.75 * duration:
            tx = -32 / 6 * (tx - 0.5) ** 3 + 2 * (tx - 0.5) + 0.5
        else:
            tx = 32 / 6 * (tx - 0.75) ** 3 - 4 * (tx - 0.75) ** 2 + (tx - 0.75) + 11 / 12
        x_array = start * (1 - tx) + end * tx
        x_angles = inverse_kinematics(x_array)
    else:
        x_angles = inverse_kinematics(end)
    return x_angles

五次多项式：规划位置 & 速度 & 加速度

思路比较类似。

\[ \phi(t) = a_0 + a_1t + a_2t^2 + a_3t^3 + a_4t^4 + a_5t^5 \]

六个未知数 , 就可以指定起点终点的位置、速度、加速度，然后求解方程。

quintic_polynomial
def quintic_polynomial(start, end, t, duration):
    """
    五次多项式轨迹规划
    :param start: 起始点坐标
    :param end: 终点坐标
    :param t: 当前时间
    :param duration: 总时长
    :return: 当前时刻的位置
    """
    if t < duration:
        t_matrix = np.matrix([
            [0, 0, 0, 0, 0, 1],
            [duration ** 5, duration ** 4, duration ** 3, duration ** 2, duration, 1],
            [0, 0, 0, 0, 1, 0],
            [5 * duration ** 4, 4 * duration ** 3, 3 * duration ** 2, 2 * duration, 1, 0],
            [0, 0, 0, 2, 0, 0],
            [20 * duration ** 3, 12 * duration ** 2, 6 * duration, 2, 0, 0]
        ])
        x_matrix = np.matrix([[start[i], end[i], 0, 0, 0, 0] for i in range(len(start))]).T
        k_matrix = np.linalg.inv(t_matrix) @ x_matrix
        time_vector = np.matrix([t ** 5, t ** 4, t ** 3, t ** 2, t, 1]).T
        x = (k_matrix.T @ time_vector).T.A[0]
    else:
        x = end
    return x

直线段 + 抛物线过渡

两段形状相同的抛物线，中间连接的直线段是公切线

  • 过渡段：抛物线段
  • 直线段：顾名思义

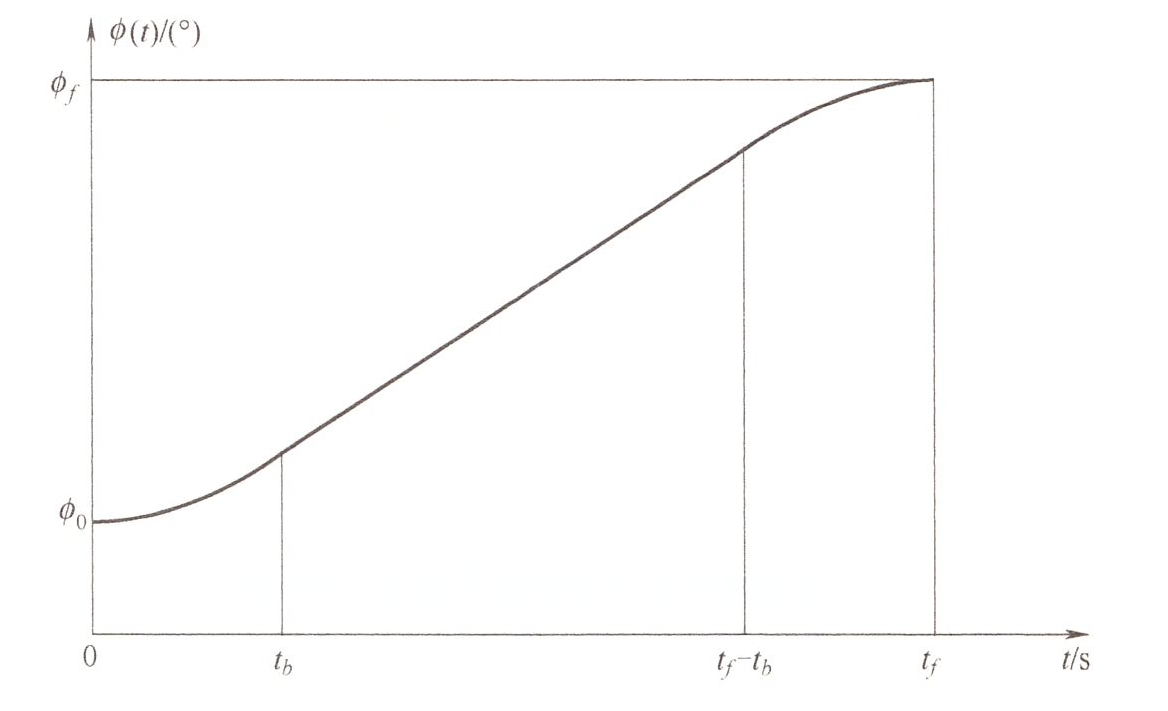
给定：起点 \(\phi_0\)、终点 \(\phi_{final}\)、总时间 \(t_{final}\)、加速度 \(\ddot\phi\) 需要求解：过渡时间（抛物线段）\(t_b\)、速度（直线段）\(k_b\)

\[ t_b=\frac{\ddot{\phi}t_f-\sqrt{\ddot{\phi}^2t_f^2-4\ddot{\phi}(\phi_f-\phi_0)}}{2\ddot{\phi}} \]

过渡段的时间间隔，二次方程求根公式求解。舍掉 + 号的解是因为 \(t_b < t_{f}\)

\[ k_b=\ddot \phi \cdot t_b \]

这里相当于初速度为 0 的平抛

parabolic_transition
def parabolic_transition(start, end, t, duration):
    """
    抛物线过渡插值
    :param start: 起始点坐标
    :param end: 终点坐标
    :param t: 当前时间
    :param duration: 总时长
    :return: 当前时刻的位置
    """
    if t < duration:
        tx = t / duration
        if t < 0.5 * duration:
            tx = 2 * (tx ** 2)
        else:
            tx = 0.5 + 2 * (tx - 0.5) - 2 * (tx - 0.5) ** 2
        x_array = start * (1 - tx) + end * tx
        x_angles = inverse_kinematics(x_array)
    else:
        x_angles = inverse_kinematics(end)
    return x_angles

中间点 + 抛物线过渡

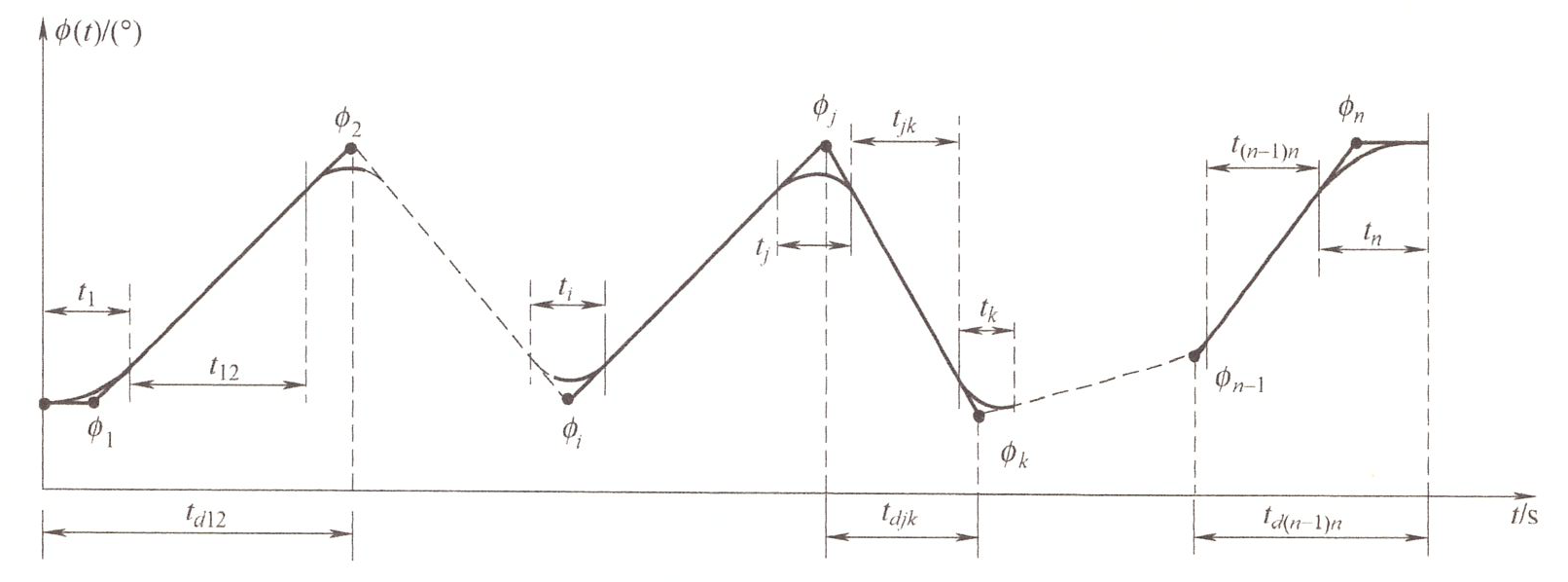
给定： 系列点 \(\phi_0, \phi_1,\dots,\phi_{final}\)、各段时间 \(t_{dij}\)、加速度 \(\ddot\phi\)

需要求解： 各段的速度 \(k_{ij}\)，以及过渡段的时间 \(t_{i}\)，直线段的时间 \(t_{ij}\)

中间段计算

过渡段 \( j \) 加速度

\[ \ddot{\phi}_j = \text{SGN}(\dot{\phi}_{jk} - \dot{\phi}_{ij}) \cdot |\ddot{\phi}_j| \]

过渡段 \( j \) 时间间隔

\[ t_j = \frac{\dot{\phi}_{jk} - \dot{\phi}_{ij}}{\ddot{\phi}_j} \]

直线段 \( jk \) 速度

\[ \dot{\phi}_{jk} = \frac{\phi_k - \phi_j}{t_{djk}} \]

直线段时间 \( jk \) 间隔

\[ t_{jk} = t_{djk} - \frac{1}{2} t_j - \frac{1}{2} t_k \]
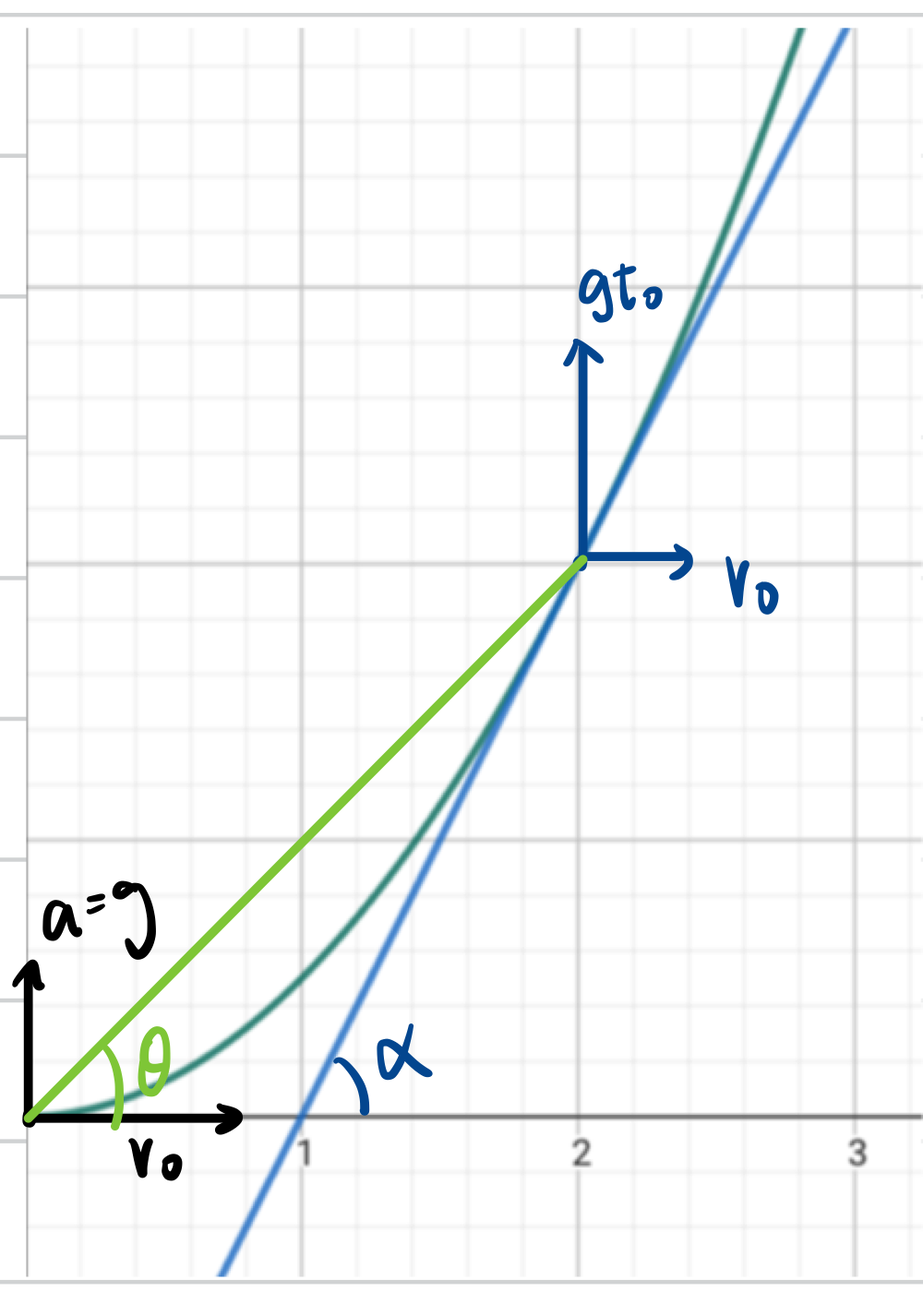
为什么是 \(\frac{1}{2}t\)

这里可以联想到高中平抛运动当中的知识，速度角和位置角有一个 \(\frac{1}{2}\) 的关系。

这个其实很容易推导：

  1. 速度角：\(\tan \alpha = \frac{v_y}{v_x}= \frac{g\cdot t}{v_0}\)
  2. 位置角：\(\tan \theta = \frac{y}{x} = \frac{\frac{1}{2}g\cdot t^2}{v_0\cdot t} = \frac{1}{2}\cdot \tan \alpha\)

也就是说，任意给定抛物线上的点，找到位移中点，连线即可得到速度方向

起始段计算

过渡段 1 加速度

\[ \ddot{\phi}_1 = \text{SGN}(\phi_2 - \phi_1) \cdot |\ddot{\phi}_1| \]

过渡段 1 时间间隔

根据切点速度相等列写方程

\[ \frac{\phi_2 - \phi_1}{t_{d12} - \frac{1}{2} t_1} = \ddot{\phi}_1 t_1 \]

求根公式解得：

\[ t_1 = t_{d12} - \sqrt{t_{d12}^2 - \frac{2(\phi_2 - \phi_1)}{\ddot{\phi}_1}} \]

直线段 12 速度

\[ \dot{\phi}_{12} = \frac{\phi_2 - \phi_1}{t_{d12} - \frac{1}{2} t_1} \]

直线段 12 时间间隔

\[ t_{12} = t_{d12} - t_1 - \frac{1}{2} t_2 \]

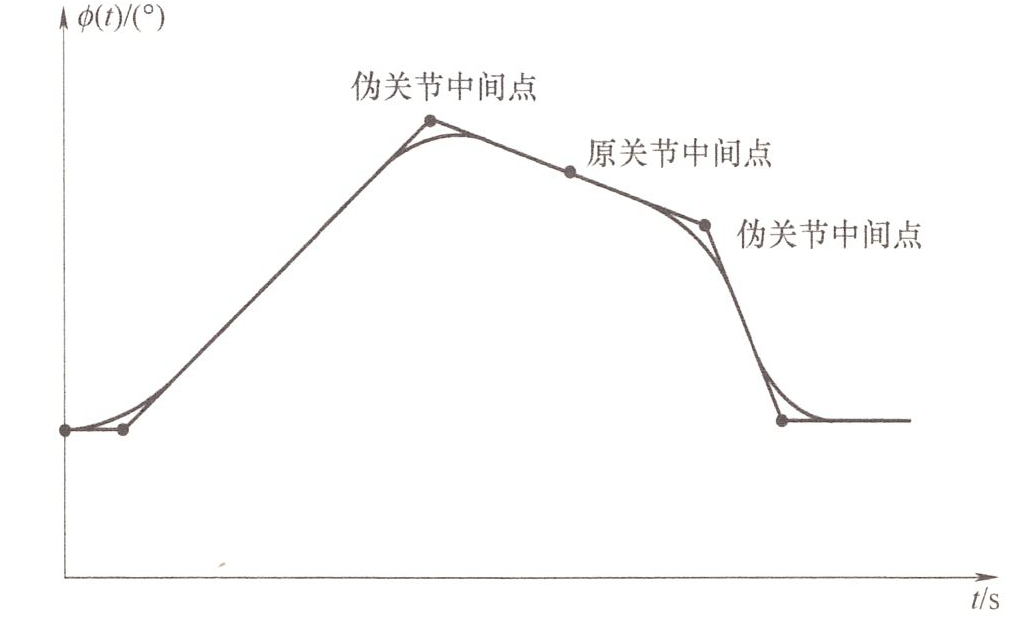
这里因为抛物线对轨迹进行了圆滑处理，相当于先用直线连接起来，再用抛物线做一个圆角，所以并不能真正到达对应的点

解决方案：设置两个伪关节，连线经过给定点，则可以保证经过给定点

笛卡尔空间规划

旋转矩阵和欧拉角不可以插值的原因：插值得到的 R 矩阵不一定属于 SO(3)

等效轴角插值

Slerp ｜ 四元数球面线性插值

\[ r_t = k_0 r_0 + k_1 r_1 \]
\[ \begin{align*} k_0 = \frac{\sin((1-t)\theta)}{\sin\theta} \quad k_1 = \frac{\sin(t\theta)}{\sin\theta},\theta = \cos^{-1}(r_0 \cdot r_1) \end{align*} \]
证明

\(S^3\) 中的单位四元数 \(\eta + i\varepsilon_1 + j\varepsilon_2 + k\varepsilon_3\) 与 \(\mathrm{U}\) 中的欧拉参数 \((\eta, \varepsilon_1, \varepsilon_2, \varepsilon_3)^T\) 一一对应。考虑两个用欧拉参数（等价于用单位四元数）表示的不同姿态：

\[ \mathbf{r}_0 = (\eta, \varepsilon_1, \varepsilon_2, \varepsilon_3)^T \]
\[ \mathbf{r}_1 = (\xi, \delta_1, \delta_2, \delta_3)^T \]

式中，\(\mathbf{r}_0 \neq \mathbf{r}_1\) 且 \(\mathbf{r}_0 \neq -\mathbf{r}_1\)。四元数插值的目的是找出中间姿态 \(\mathbf{r}_t\)，\(t \in [0, 1]\)（注意这里的起止时间作了归一化），使得 \(\mathbf{r}_0\) 平滑过渡到 \(\mathbf{r}_1\)。显然，\(\mathbf{r}_0\) 和 \(\mathbf{r}_1\) 这两个四维单位向量确定了 \(\mathbb{R}^4\) 中的一个平面，该平面上的任何一个元素（四维向量）都可以表示为 \(\mathbf{r}_0\) 和 \(\mathbf{r}_1\) 的线性组合。在该平面中，向量 \(\mathbf{r}_0\)、\(\mathbf{r}_1\) 和 \(\mathbf{r}_0 - \mathbf{r}_1\) 构成一个三角形，对于 \(\mathbf{r}_0\) 和 \(\mathbf{r}_1\) 的夹角 \(\theta\)，由余弦定理，有

\[ 2\|\mathbf{r}_0\|\|\mathbf{r}_1\|\cos\theta = \|\mathbf{r}_0\|^2 + \|\mathbf{r}_1\|^2 - \|\mathbf{r}_0 - \mathbf{r}_1\|^2 \]

注意到 \(\|\mathbf{r}_0\| = \|\mathbf{r}_1\| = 1\)。

\[ \begin{align*} \|\mathbf{r}_0 - \mathbf{r}_1\|^2 &= (\eta - \xi)^2 + (\varepsilon_1 - \delta_1)^2 + (\varepsilon_2 - \delta_2)^2 + (\varepsilon_3 - \delta_3)^2\\ &= (\eta^2 + \varepsilon_1^2 + \varepsilon_2^2 + \varepsilon_3^2) + (\xi^2 + \delta_1^2 + \delta_2^2 + \delta_3^2) - 2(\eta\xi + \varepsilon_1\delta_1 + \varepsilon_2\delta_2 + \varepsilon_3\delta_3)\\ &= \|\mathbf{r}_0\|^2 + \|\mathbf{r}_1\|^2 - 2\mathbf{r}_0 \cdot \mathbf{r}_1 \end{align*} \]

于是，两个欧拉参数的内积等于它们夹角的余弦值

\[ \mathbf{r}_0 \cdot \mathbf{r}_1 = \cos\theta \]

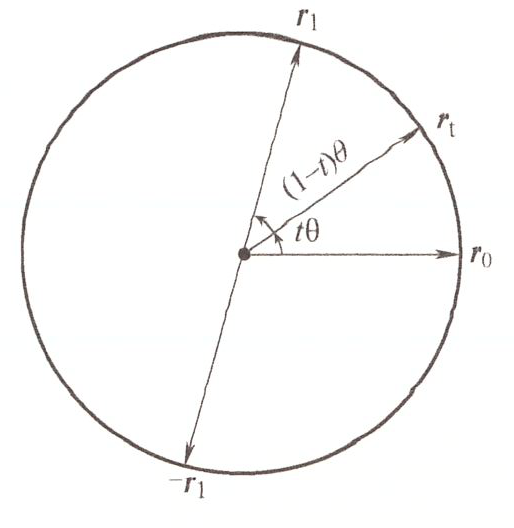
如图所示，将中间姿态 \(\mathbf{r}_t\) 限制在 \(\mathbf{r}_0\) 和 \(\mathbf{r}_1\) 确定的平面中并假设匀速旋转，可以使四元数插值问题化为一个简单的平面几何问题：\(\mathbf{r}_0\)、\(\mathbf{r}_1\) 和 \(\mathbf{r}_t\) 都在平面单位圆上，\(\mathbf{r}_t\) 从 \(\mathbf{r}_0\) 匀速旋转到 \(\mathbf{r}_1\)。

由于匀速旋转，对于 \(t \in [0, 1]\)，\(\mathbf{r}_0\) 与 \(\mathbf{r}_t\) 的夹角是 \(t\theta\)，\(\mathbf{r}_1\) 与 \(\mathbf{r}_t\) 的夹角是 \((1-t)\theta\)，则由欧拉参数内积与夹角余弦值的关系，有

\[ \begin{align*} \mathbf{r}_0 \cdot \mathbf{r}_t = \cos(t\theta)\\ \mathbf{r}_t \cdot \mathbf{r}_1 = \cos((1-t)\theta) \end{align*} \]

同时，\(\mathbf{r}_t\) 可以表示为 \(\mathbf{r}_0\) 和 \(\mathbf{r}_1\) 的线性组合，即

\[ \mathbf{r}_t = k_0\mathbf{r}_0 + k_1\mathbf{r}_1 \]

最后，求解线性方程组

\[ \begin{cases} k_0 + k_1\cos\theta = \cos(t\theta) \\ k_0\cos\theta + k_1 = \cos((1-t)\theta) \end{cases} \]

联立两式，可求得

\[ k_0 = \frac{\sin((1-t)\theta) - k_1\sin\theta}{\sin\theta}, k_1 = \frac{\sin(t\theta) - k_0\sin\theta}{\sin\theta} \]

式中，\(\theta = \cos^{-1}(\mathbf{r}_0 \cdot \mathbf{r}_1)\)。

slerp_interpolation
def slerp(q1, q2, t):
    """
    球面线性插值（Slerp）
    :param q1: 起始四元数
    :param q2: 终止四元数
    :param t: 插值因子，范围 [0, 1]
    :return: 插值后的四元数
    """
    dot_product = np.dot(q1, q2)
    dot_product = np.clip(dot_product, -1.0, 1.0)
    theta_0 = np.arccos(dot_product)
    sin_theta_0 = np.sin(theta_0)
    
    if sin_theta_0 < 1e-6:
        return q1
    
    theta = theta_0 * t
    s1 = np.sin(theta) / sin_theta_0
    s0 = np.cos(theta) - dot_product * s1
    return s0 * q1 + s1 * q2

有约束的轨迹规划

避障

加速度 / 速度限制

题型

多项式参数计算：时间、速度

抛物线过渡计算

matlab 求解方程