03 | 逆运动学 - 已知位姿求解角度 ¶

约 4275 个字 1 行代码预计阅读时间 17 分钟

为什么需要逆运动学：想控制的量一般在操作空间，而被控量是关节空间

本章内容：给定工具坐标系的位置和姿态，解算出个各关节变量；把笛卡尔空间转换到关节空间

主要内容：

数学基础：三角变换 ¶

诱导公式和角公式倍角公式半角公式和差化积公式万能公式辅助角公式

奇变偶不变，符号看象限，即形如 \((2k + 1)\cdot90\pm\alpha\)

\(\sin(\alpha + \beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)
\(\sin(\alpha - \beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\)
\(\cos(\alpha + \beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)
\(\cos(\alpha - \beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
\(\tan(\alpha + \beta)=\frac{\tan\alpha+\tan\beta}{1 - \tan\alpha\tan\beta}\)
\(\tan(\alpha - \beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\)

\(\sin2\alpha = 2\sin\alpha\cos\alpha\)
\(\cos2\alpha=\cos^{2}\alpha-\sin^{2}\alpha = 2\cos^{2}\alpha - 1 = 1 - 2\sin^{2}\alpha\)
\(\tan2\alpha=\frac{2\tan\alpha}{1 - \tan^{2}\alpha}\)

\(\sin\frac{\alpha}{2}=\pm\sqrt{\frac{1 - \cos\alpha}{2}}\)
\(\cos\frac{\alpha}{2}=\pm\sqrt{\frac{1+\cos\alpha}{2}}\)
\(\tan\frac{\alpha}{2}=\pm\sqrt{\frac{1 - \cos\alpha}{1+\cos\alpha}}=\frac{\sin\alpha}{1+\cos\alpha}=\frac{1 - \cos\alpha}{\sin\alpha}\)

高中搜到一个口诀感觉特别形象，这里记一下

\(\sin\alpha+\sin\beta = 2\sin\frac{\alpha + \beta}{2}\cos\frac{\alpha - \beta}{2}\) 帅 + 帅 = 帅哥
\(\sin\alpha-\sin\beta = 2\cos\frac{\alpha + \beta}{2}\sin\frac{\alpha - \beta}{2}\) 帅 - 帅 = 哥帅
\(\cos\alpha+\cos\beta = 2\cos\frac{\alpha + \beta}{2}\cos\frac{\alpha - \beta}{2}\) 哥 + 哥 = 哥哥
\(\cos\alpha-\cos\beta=-2\sin\frac{\alpha + \beta}{2}\sin\frac{\alpha - \beta}{2}\) 哥 - 哥 = 负嫂嫂

\(\sin\alpha=\frac{2\tan\frac{\alpha}{2}}{1 + \tan^{2}\frac{\alpha}{2}}\)
\(\cos\alpha=\frac{1-\tan^{2}\frac{\alpha}{2}}{1 + \tan^{2}\frac{\alpha}{2}}\)
\(\tan\alpha=\frac{2\tan\frac{\alpha}{2}}{1-\tan^{2}\frac{\alpha}{2}}\)

\(a\sin\alpha + b\cos\alpha=\sqrt{a^{2}+b^{2}}\sin(\alpha + \varphi)\)，其中 \(\tan\varphi=\frac{b}{a}\)

正弦定理

\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\)

余弦定理

\(a^{2}=b^{2}+c^{2}-2bc\cos A\)
\(b^{2}=a^{2}+c^{2}-2ac\cos B\)
\(c^{2}=a^{2}+b^{2}-2ab\cos C\)

反正切 arctan2 ¶

arctan2 arctan 的局限性

\(\arctan2(y, x)\) 函数接受两个参数（\(y\) 和 \(x\)），而不是它们的比值，具有以下优势：

能够正确区分四个象限
可以处理 \(x = 0\) 的情况
结果范围为 \((-\pi, \pi]\)，覆盖完整的角度范围

arctan 的局限性：只有一个参数 \(\frac{y}{x}\)，丢失了象限信息

无法区分象限：例如 \(\arctan(\frac{1}{1}) = \arctan(\frac{-1}{-1}) = \frac{\pi}{4}\)，但这两个点实际上在不同象限
当 \(x = 0\) 时无法计算（除零错误）
结果范围仅为 \((-\frac{\pi}{2}, \frac{\pi}{2})\)，不能表示完整的 360° 范围

定义如下：

\[ \text{arctan2}(y, x) = \begin{cases} \arctan(y/x) & \text{if } x > 0 \\ \arctan(y/x) + \pi & \text{if } x < 0 \text{ and } y \geq 0 \\ \arctan(y/x) - \pi & \text{if } x < 0 \text{ and } y < 0 \\ +\pi/2 & \text{if } x = 0 \text{ and } y > 0 \\ -\pi/2 & \text{if } x = 0 \text{ and } y < 0 \\ \text{undefined} & \text{if } x = 0 \text{ and } y = 0 \end{cases} \]

工作空间与自由度 ¶

自由度｜ Degrees of Freedom¶

自由度 - 刚体本身具有可独立运动方向的数目

手臂：7 自由度；无穷多个解腿：6自由度;8个解

\[ F = 6(l - n - 1)+\sum_{i = 1}^{n}f_{i} \\ l为连杆数（包括基座），n为关节总数，f_i为第i个关节的自由度数 \]

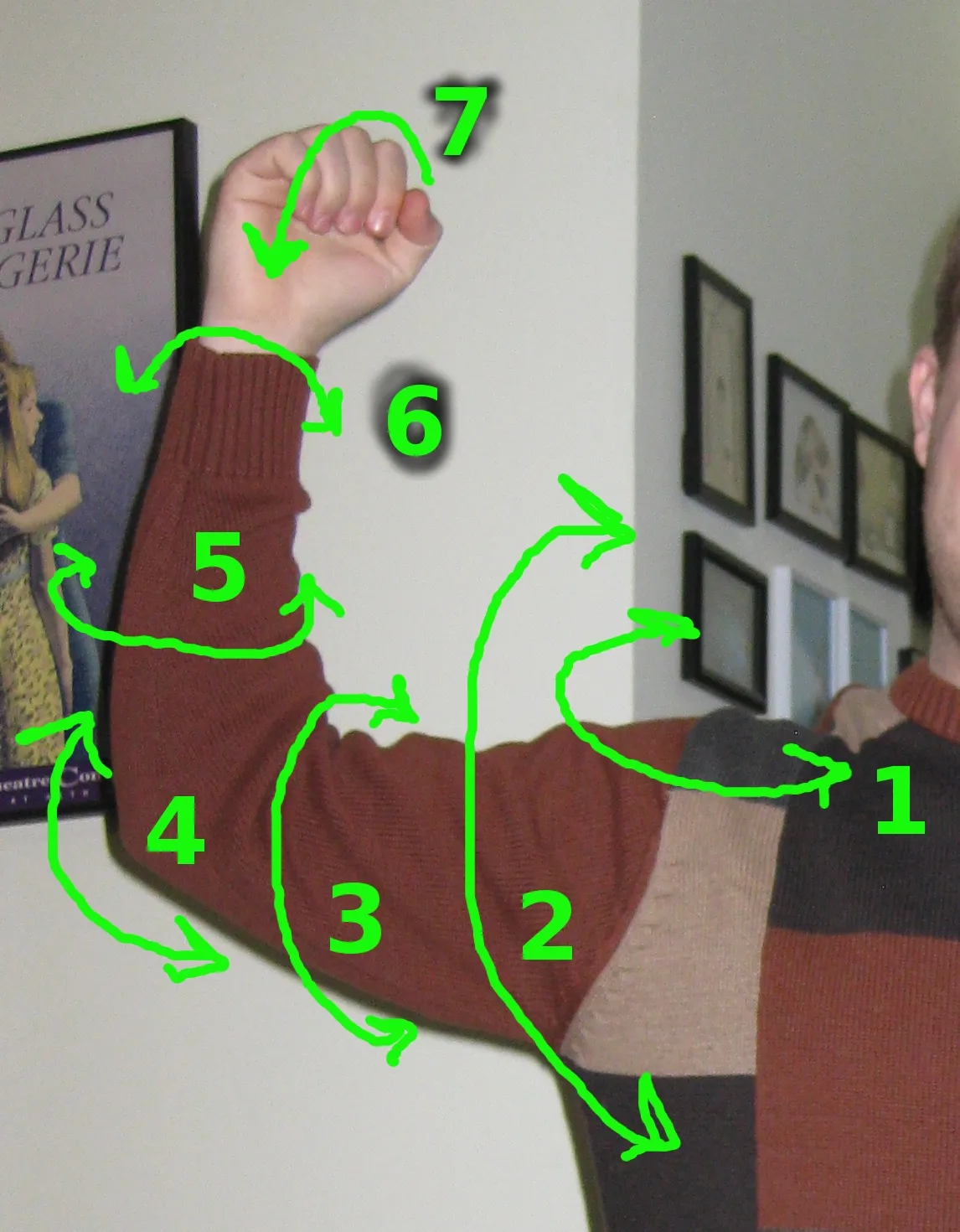
一个 6 自由度的机械手，即使某两组构型对应的末端机构的三维位置相同，机械手在从一个构型移动到另一个构型的时候无法保持末端机构始终不动。

如果有人在电视里看过工业机器人焊东西的话，就会发现它在同一个位置焊接的时候，一会儿整个扭到这边，一会儿整个扭到那边，看起来非常酷炫的样子。事实上这么做只是因为，虽然焊接只是想改变末端机构的朝向，而不改变末端机构的位置，但是由于定理的限制，它必须要往后退一些，然后各种扭，才能保证在移动末端机构的朝向的过程中不会撞到东西，因为移动的时候末端机构的三维位置一定会乱动。如果它能够随便转一点点就可以达到目的，还费那个力气酷炫地整体都转起来干啥……

而多了一个自由度以后就不一样了。

想想开门时拧钥匙的动作，这个情况下是人胳膊的末端机构（手）的三维位置没有变（始终在钥匙孔前），但是末端机构（手）的三维旋转变了（转动了钥匙）。人能够实现这个简单的动作，就是因为我们的胳膊有 7 个自由度。

工作空间｜ Workspace¶

工作空间：机械臂末端执行器所能到达的范围。
灵巧工作空间：机械臂末端执行器能够从各个方向到达的空间区域。
可达工作空间：机械臂末端执行器至少从一个方向上可以到达的空间。

通常机械臂的关节越多，机械臂的自由度就越高，那么可达工作空间往往就越大，当机械臂少于 6 个自由度时，它就不能达到三维空间内一般的目标点。

如何描述工作空间

解存在性与选择 ¶

\(^0_6 \!T\) 自由度为 6 个

由于是 nonlinear transcendental equations( 非线性超越方程组 ) 问题，6 未知数 6 方程式不代表具有唯一解。

PIEPER 准则 ¶

当如下条件之一满足时，一个 6 自由度运动学结构具有闭合形式的运动学逆解：（充分条件）

1、三个连续的转动关节的轴相交于同一点 2、三个连续的转动关节的轴平行

多解处理方法 —— 最短行程 ¶

若同一位姿有多个解，系统最终只能选择一个解，比较合理的一种选择是取“最短行程”解

计算最短行程需要加权，倾向于选择移动小连杆而不是移动大连杆（更省能量）

例子

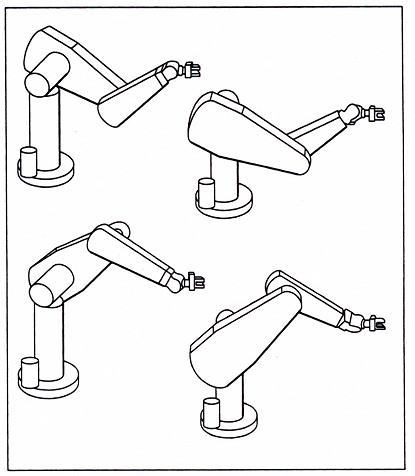
图片来源课程组 ppt

这四个姿态位姿都相同，但是对于每种手部都有 2 种解，一共有 8 个解。

几何法 - 引入几何方法 ¶

由于操作臂是平面的，因此可利用平面几何关系直接求解

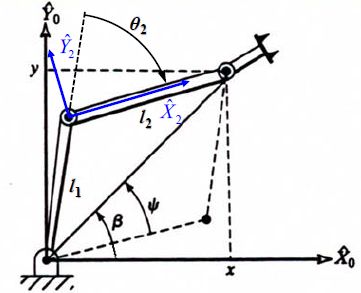
注意到三个连杆角度之和即为连杆 3 的姿态：\(\theta_1 + \theta_2 + \theta_3 = \phi\), 由此可求得 \(\theta_3\)。

应用反正切公式：\(\beta = \arctan 2(y, x)\)

应用余弦定理：\(\cos \psi = \frac{x^2 + y^2 + l_1^2 - l_2^2}{2l_1 \sqrt{x^2 + y^2}}\)

可解得 \(\psi \in [0^\circ, 180^\circ]\)

进一步，可得：

\[ \theta_1 = \begin{cases} \beta + \psi, & \text{若 } \theta_2 \leq 0 \\ \beta - \psi, & \text{若 } \theta_2 > 0 \end{cases} \]

特别要注意这个是平行四边形，而不是菱形，所以两种情况用的证明三角形略有不同，但是结论是统一的。

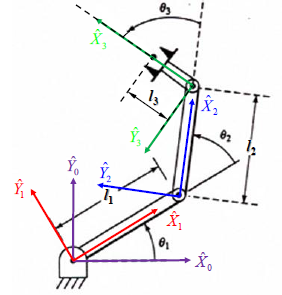
解析（代数）法 - 解析表达式表出 ¶

工业上很多特定的机械臂也都是解析法求解

机器人的运动学解——逆向运动学解 - 知乎

基础代数 ¶

核心思想：同一变量不同表出列方程

例 1 基础的平面 3 自由度机械臂 ¶

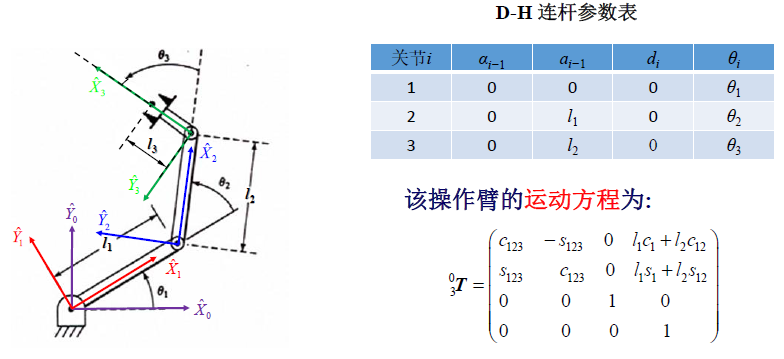
图片来源课程组 ppt

该操作臂的逆运动学问题可描述为：

\[ {}^0_3 \mathbf{T} = \begin{pmatrix} c_{123} & -s_{123} & 0 & l_1 c_1 + l_2 c_{12} \\ s_{123} & c_{123} & 0 & l_1 s_1 + l_2 s_{12} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} c_{\phi} & -s_{\phi} & 0 & x \\ s_{\phi} & c_{\phi} & 0 & y \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \]

得到四个非线性方程：

\[ \begin{cases} x = l_1 c_1 + l_2 c_{12} \\ y = l_1 s_1 + l_2 s_{12} \end{cases} \]

其中：

\[ \begin{cases} c_{\phi} = c_{123} \\ s_{\phi} = s_{123} \end{cases} \]

推导得到：

\[ \begin{align} x^2 + y^2 &= l_1^2 + l_2^2 + 2l_1 l_2 (c_1 c_{12} + s_1 s_{12})\\ &= l_1^2 + l_2^2 + 2l_1 l_2 (c_1^2 c_2 - c_1 s_1 s_2 + s_1^2 c_2 + s_1 c_1 s_2)\\ &= l_1^2 + l_2^2 + 2l_1 l_2 c_2 \end{align} \]

\[ c_2 = \frac{x^2 + y^2 - l_1^2 - l_2^2}{2l_1 l_2} \]

若 \(-1 \leq c_2 \leq 1\)，上式有解；否则无解。

若上式有解，则：

\[ s_2 = \pm \sqrt{1 - c_2^2} \quad, \quad \theta_2 = \arctan 2(s_2, c_2) \]

得到 2 个可行的 \(\theta_2\)( 肘上形和肘下形 )

三角函数方程式 ¶

\(n\) 不大于 4 时，一元 \(n\) 次方程有封闭形式的解

有些情况下可将超越方程化为一元 n 次方程

例：求解超越方程 \(a \cos \theta + b \sin \theta = c\) 的 \(\theta\)

解：利用

\[ \cos \theta = \frac{1 - u^2}{1 + u^2} \quad , \quad \sin \theta = \frac{2u}{1 + u^2} \]

得到

\[ a(1 - u^2) + 2bu = c(1 + u^2)\\ (a + c)u^2 - 2bu + (c - a) = 0 \]

得到

\[ u = \frac{b \pm \sqrt{b^2 + a^2 - c^2}}{a + c} \quad , \quad \theta = 2 \arctan \left( \frac{b \pm \sqrt{b^2 + a^2 - c^2}}{a + c} \right) \]

如果 \(a + c = 0\)，那么 \(\theta = 180^\circ\)

3 轴相交 PIEPER 解法 ¶

具有 6 个旋转关节的操作臂存在封闭解的充分条件是相邻的三个关节轴线相交于一点

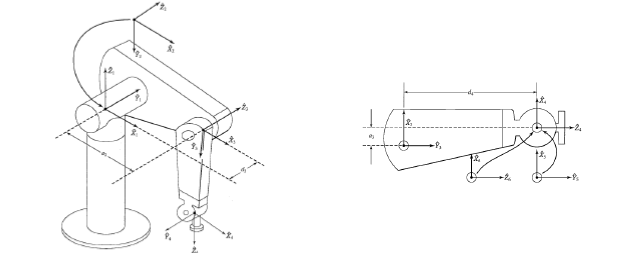
当最后 3 根轴相交时，连杆坐标系 {4}、{5}、{6} 的原点均位于这个交点上 ( 齐次变换矩阵当中的 \(\vec{P}\) 是一个值，但是 \(\mathbb{R}\) 是不一样的 )，这点的基坐标为：

\[ \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = {}^0_1 \mathbf{T} {}^1_2 \mathbf{T} {}^2_3 \mathbf{T} \begin{pmatrix} {}^3 \mathbf{O}_4 \\ 1 \end{pmatrix} \]

其中：

\[ \begin{pmatrix} {}^2 \mathbf{O}_4 \\ 1 \end{pmatrix} = {}^2 \mathbf{T} \begin{pmatrix} {}^3 \mathbf{O}_4 \\ 1 \end{pmatrix} = \begin{pmatrix} c \theta_3 & -s \theta_3 & 0 & a_2 \\ s \theta_3 c \alpha_2 & c \theta_3 c \alpha_2 & -s \alpha_2 & -s \alpha_2 d_3 \\ s \theta_3 s \alpha_2 & c \theta_3 s \alpha_2 & c \alpha_2 & c \alpha_2 d_3 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} f_1(\theta_3) \\ f_2(\theta_3) \\ f_3(\theta_3) \\ 1 \end{pmatrix} \]

其中：

\[ \begin{align} f_1 &= f_1(\theta_3) = a_3 c_3 + d_4 s \alpha_3 s_3 + a_2\\ f_2 &= f_2(\theta_3) = a_3 c \alpha_2 s_3 - d_4 s \alpha_2 c \alpha_3 c_3 - d_4 s \alpha_2 c \alpha_3 s \alpha_3 - d_3 s \alpha_2\\ f_3 &= f_3(\theta_3) = a_3 s \alpha_2 s_3 - d_4 s \alpha_2 s \alpha_2 c \alpha_3 + d_4 c \alpha_2 c \alpha_3 + d_3 c \alpha_2 \end{align} \]

利用 \({}^0_1 \mathbf{T}\)，\({}^1_2 \mathbf{T}\)，得到：

\[ \begin{pmatrix} {}^1 \mathbf{O}_4 \\ 1 \end{pmatrix} = {}^1_2 \mathbf{T} \begin{pmatrix} {}^2 \mathbf{O}_4 \\ 1 \end{pmatrix} = \begin{pmatrix} c \theta_2 & -s \theta_2 & 0 & a_1 \\ s \theta_2 c \alpha_1 & c \theta_2 c \alpha_1 & -s \alpha_1 & -s \alpha_1 d_2 \\ s \theta_2 s \alpha_1 & c \theta_2 s \alpha_1 & c \alpha_1 & c \alpha_1 d_2 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} g_1(\theta_2, \theta_3) \\ g_2(\theta_2, \theta_3) \\ g_3(\theta_2, \theta_3) \\ 1 \end{pmatrix} \]

其中：

\[ \begin{align} g_1 &= g_1(\theta_2, \theta_3) = c_2 f_1 - s_2 f_2 + a_1\\ g_2 &= g_2(\theta_2, \theta_3) = s_2 c \alpha_1 f_1 + c_2 c \alpha_1 f_2 - s \alpha_1 f_3 - d_2 s \alpha_1\\ g_3 &= g_3(\theta_2, \theta_3) = s_2 s \alpha_1 f_1 + c_2 s \alpha_1 f_2 + c \alpha_1 f_3 + d_2 c \alpha_1 \end{align} \]

令：

\[ \begin{align} r &= x^2 + y^2 + z^2 \\ &= (c_1 g_1 - s_1 g_2)^2 + (s_1 g_1 + c_1 g_2)^2 + g_3^2\\ &= g_1^2 + g_2^2 + g_3^2 = f_1^2 + f_2^2 + f_3^2 + a_1^2 + d_2^2 + 2a_1(c_2 f_1 - s_2 f_2) \end{align} \]

求解 \(\theta_3\) 求解 \(\theta_2\) 求解 \(\theta_1\) 求解 \(\theta_4, \theta_5, \theta_6\)

简化表达，得到：

\[ r = (k_1 c_2 + k_2 s_2) 2a_1 + k_3, z = (k_1 s_2 - k_2 c_2) s \alpha_1 + k_4 \]

其中：

\[ \begin{align} k_1 &= f_1\\ k_2 &= -f_2\\ k_3 &= f_1^2 + f_2^2 + f_3^2 + a_1^2 + d_2^2 + 2d_2 f_3\\ k_4 &= f_3 c \alpha_1 + d_2 c \alpha_1 \end{align} \]

若 \(a_1 = 0\)，则：

\[ r = k_3 = f_1^2 + f_2^2 + f_3^2 + a_1^2 + d_2^2 + 2d_2 f_3 \]

注意到：

\[ \begin{align} f_1 &= f_1(\theta_3) = a_3 c_3 + d_4 s \alpha_3 s_3 + a_2\\ f_2 &= f_2(\theta_3) = a_3 s \alpha_2 s_3 - d_4 s \alpha_2 c \alpha_3 c_3 - d_4 s \alpha_2 c \alpha_3 s \alpha_3 - d_3 s \alpha_2\\ f_3 &= f_3(\theta_3) = a_3 s \alpha_2 s_3 - d_4 s \alpha_2 s \alpha_2 c \alpha_3 + d_4 c \alpha_2 c \alpha_3 + d_3 c \alpha_2 \end{align} \]

将 \(u = \tan \frac{\theta_3}{2}\)，\(c_3 = \frac{1 - u^2}{1 + u^2}\)，\(s_3 = \frac{2u}{1 + u^2}\) 代入，可将 \(r = k_3\) 化为 \(u\) 的二次方程。利用二次方程可以得到 \(\theta_3\)。

若 \(s \alpha_1 = 0\)，则 \(z = k_4\)，同样采用化简为多项式的办法，由二次方程得 \(\theta_3\)。
否则，消去 \(s_2\) 和 \(c_2\)，得到：

\[ \frac{(r - k_3)^2}{4a_1^2} + \frac{(z - k_4)^2}{s^2 \alpha_1^2} = k_1^2 + k_2^2 \]

采用化简为多项式的办法，可得到一个四次方程，由此解得 \(\theta_3\)。

根据：

\[ r = (k_1 c_2 + k_2 s_2) 2a_1 + k_3\\ z = (k_1 s_2 - k_2 c_2) s \alpha_1 + k_4 \]

可解得 \(\theta_2\)。

根据：

\[ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} c_1 g_1 - s_1 g_2 \\ s_1 g_1 + c_1 g_2 \end{pmatrix} \]

\(x\) 和 \(y\) 是已知的，可解得 \(\theta_1\)。

求出 \(\theta_1, \theta_2, \theta_3\) 后，若 \(\theta_4 = 0\) 可计算出坐标系 {4} 相对于基坐标的姿态：

\[ {}^0_4 \mathbf{R} |_{\theta_4 = 0} = {}^0_3 \mathbf{R} {}^3_4 \mathbf{R} |_{\theta_4 = 0} = {}^0_1 \mathbf{R} {}^1_2 \mathbf{R} {}^2_3 \mathbf{R} {}^3_4 \mathbf{R} |_{\theta_4 = 0} \]

再由已知的 \({}^0_6 \mathbf{R}\)，坐标系 {6} 的期望姿态与坐标系 {4} 的姿态差别仅在于最后三个关节的作用：

\[ {}^6_4 \mathbf{R} |_{\theta_4 = 0} = {}^6 \mathbf{R}^1 |_{\theta_4 = 0} {}^0 \mathbf{R}^6 \]

对于任何一个 4、5、6 轴相互正交的 6R 操作臂，最后三个关节角是一种欧拉角，即 \({}^6 \mathbf{R}^4 |_{\theta = 0}\) 可由这种欧拉角表示。这时，\(\theta_4, \theta_5, \theta_6\) 可用欧拉角解法求得。

两种解相当于是手性，右手形和左手形

PUMA560 的一种代数方法 ¶

PUMA560 是一款具有球形腕的机械臂，其关节 4、5、6 的旋转轴相交于第五个关节坐标系的原点处

这里要注意，求解 \(\theta_4\) 的时候，如果 \(\theta_5 = 0\), 那么可以看图发现，轴 4 和轴 6 是重合的，这个时候不可以唯一确定 \(\theta_4\), 所有可能的结果都可能是 \(\theta_4\) 与 \(\theta_6\) 的和或差

数值法 - 有限元或者数值逼近 ¶

优化法 (Optimization-based Solution) ¶

是把问题转化为一个优化问题求数值解。

\[ q = f^{-1}(x) \]

转化为

\[ \min_{q} e, where\quad e = (x - f(q))^2 \]

求关节位置 \(q\)，使实际末端位置 \(x\) 与正运动学算出的末端位置 \(f(q)\) 之间的差最小的问题

使用梯度下降法求解，梯度下降法是求解无约束优化问题最常用的方法之一。

数值法解方程 ¶

这里主要用到的是牛顿法

一句话简述：从一个起始解开始，使用切线逐步逼近交点

\[ x_{n+1} = x_n - J(x_n)^{-1} f(x_n) \]

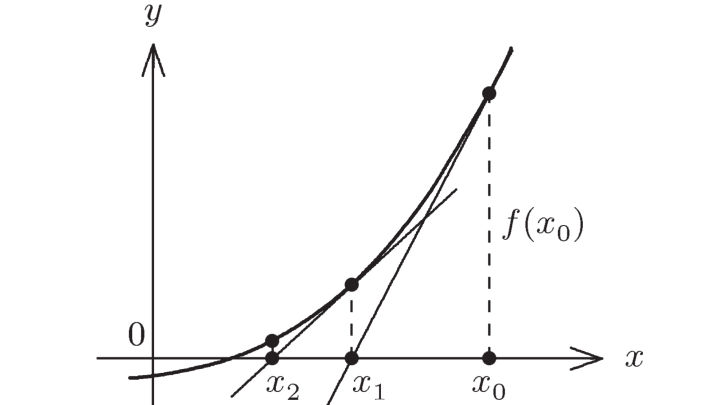
为什么这么写？

写出泰勒展开，忽略二次高阶项 . 相当于做了一条切线，再求这个切线和 x 轴的交点，得到新一轮的 x

\[ f(x) = f(x_0) + f'(x_0)(x - x_0) = 0 \]

参考资料 牛顿迭代法 - OI Wiki 牛顿法原理与应用 - CSDN博客

雅可比方法 ¶

求逆 ¶

\[ \dot{x} = J(q) \dot{q} \]

\[ \dot{q} = J(q)^{-1} \dot{x} \]

逆微分求解：已知

满秩矩阵，直接求解雅可比矩阵的逆

对于不满秩的矩阵来说，求取伪逆

对于机械臂来说，操作空间维度相当于 \(m\)，关节数目相当于 \(n\)（自变量数目）

左逆右逆

仅当 \(m \geq n\) 时 ("Tall matrix")，说明这个时候方程的数目大于未知数的个数，方程是过定 (overdetermined) 的。矩阵 \(A\) 可能有左逆矩阵

\[ A^\dagger_L = \left(A^HA\right)^{-1}A^H \]

左逆列满秩的时候一定存在

超定方程最小二乘解

仅当 \(m \leq n\) 时 ("fat matrix")，方程数目小于未知数的个数，方程式欠定的。矩阵 \(A\) 可能有右逆矩阵

\[ A^\dagger_R = A^H\left(AA^H\right)^{-1} \]

右逆行满秩的时候一定存在

欠定方程最小范数解

关于最小二乘和最小范数解的证明可以看线性方程组的最小二乘解和最小范数解 - 一以知行

\[ \forall\dot{q}_0,J(I-J^\dagger J)\dot{q}_0=0 \]

这说明矩阵 \(I-J^\dagger J\) 可以把任意关节速度投影到 " 零空间 " 内，投影后的关节速度将不改变末端执行器的位置。

利用这个特性，我们可以在满足了位置跟踪任务之后，再利用零空间实现其它任务 ( 比如避开障碍物 )。

力域转置 ¶

利用

\[ \tau = J^T(q) f \]

不关心动力学特性，把上面式子改写成

这里没懂

\[ \dot{q} = J(q)^T \dot{x} \]

阻尼最小二乘法 ¶

干货 | “逆运动学”——从操作空间到关节空间（下篇） - 知乎

迭代求解 ¶

利用雅可比关系和计算出的 \(\dot{x}\)，可以迭代求解出 \(\dot{q}\)

使用控制器控制关节速度 \(\dot{q}\)

干货 | “逆运动学”——从操作空间到关节空间（上篇） - 知乎

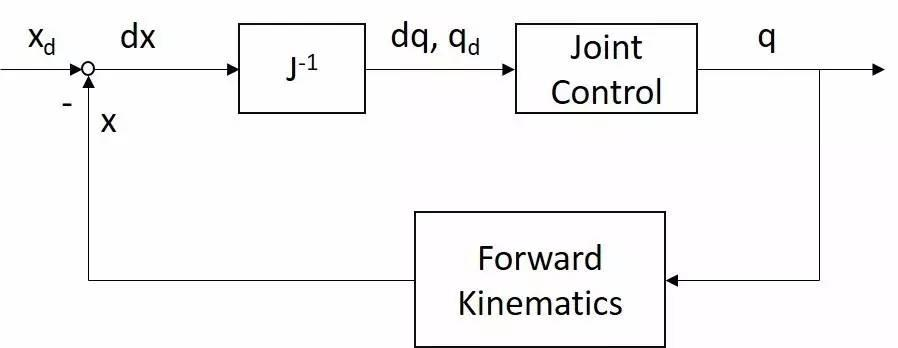
求解代码 ¶

基于 ZJUI 的代码

求解代码

03 | 逆运动学 - 已知位姿求解角度 ¶

数学基础：三角变换 ¶

反正切 arctan2 ¶

工作空间与自由度 ¶

自由度 ｜ Degrees of Freedom¶

工作空间 ｜ Workspace¶

解存在性与选择 ¶

PIEPER 准则 ¶

多解处理方法 —— 最短行程 ¶

几何法 - 引入几何方法 ¶

解析（代数）法 - 解析表达式表出 ¶

基础代数 ¶

例 1 基础的平面 3 自由度机械臂 ¶

三角函数方程式 ¶

3 轴相交 PIEPER 解法 ¶

PUMA560 的一种代数方法 ¶

数值法 - 有限元或者数值逼近 ¶

优化法 (Optimization-based Solution) ¶

数值法解方程 ¶

雅可比方法 ¶

求逆 ¶

力域转置 ¶

阻尼最小二乘法 ¶

迭代求解 ¶

求解代码 ¶

自由度｜ Degrees of Freedom¶

工作空间｜ Workspace¶