00 | 课程大纲与复习 ¶

left undone

• 四元数可视化理解
• 叉乘的矩阵形式
• 相似矩阵如何理解
• arctan2
• 如何描述工作空间
• 自由度的理解
• 奇异性的理解
• DH 参数表下计算齐次变换矩阵
• 惯性张量、转动惯量、惯量积的计算和关系
• 逆运动学求解的题目
• 末端给了力求解关节力矩的题目
• 小测题目
• 动力学模型各个矩阵的含义
• 设计控制器

三轴相交是逆运动学有解析解的充分条件

错误，连续三个 R

对于 6 自由度操作臂来说，当存在几个正交关节轴或者有多个 \(\alpha_i\) 为 0 或 ±90° 才有解析解

有 6 个旋转关节的操作譬存在封闭解的充分条件是相邻的 3 个关节轴线相交于一点

：下列说法错误的是

A. 旋转矩阵特征值均为 1

B. 旋转矩阵行列式为1
C. 旋转矩阵列向量相互正交
D. 旋转矩阵列向量为单位向量

A

填空题 1：线加速度公式

填空题 2：齐次变换矩阵求逆

填空题 3：旋转矩阵转四元数

大题 1：给定一个 DH 参数表，求 \(^0_2T\)

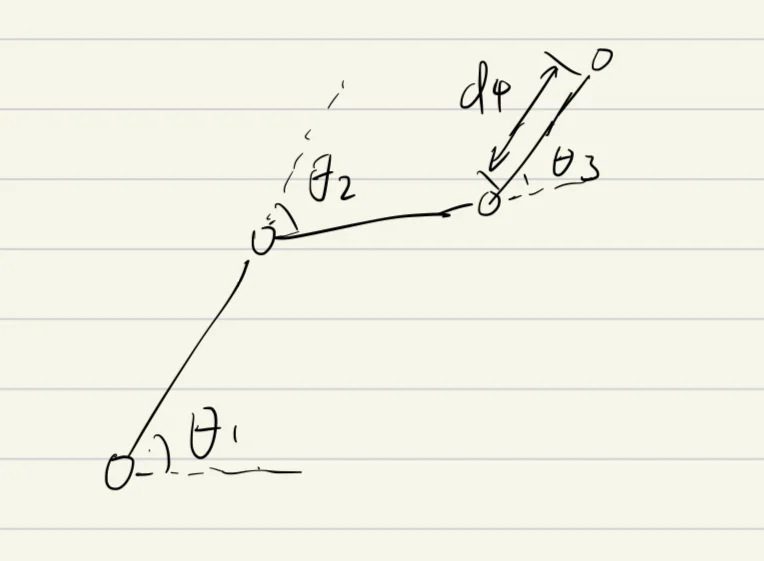
大题 2：平面三连杆，\(\theta_2\)，\(\theta_3\) 为定值，1 为转动关节，4 为移动关节

（1）求末端速度
（2）求奇异位形
（3）机械臂末端给一个力，\(f_x\)，\(f_y\)给定，给一个z轴力矩，求关节力矩

大题 3：四元数插值

（1）请描述四元数插值与欧拉角插值的优势与劣势
（2）给定初始和结束两个q，slerp插值，\(q_0 = [\frac{1}{2},\frac{1}{2},\frac{1}{2},\frac{1}{2}]\) \(q_1 = [\frac{\sqrt{3}-1}{4}, -\frac{\sqrt{3}+1}{4}, -\frac{\sqrt{3}+1}{4}, \frac{\sqrt{3}-1}{4}]\)
（3）要求角速度初始结束为0，中间段为常数，角速度连续，进行规划

大题 4：计算转动惯量，质量为 m，坐标系建在质心 \(\rho = k(\frac{l^2}{4} - x^2)\)

（1）求 k
（2）求转动惯量

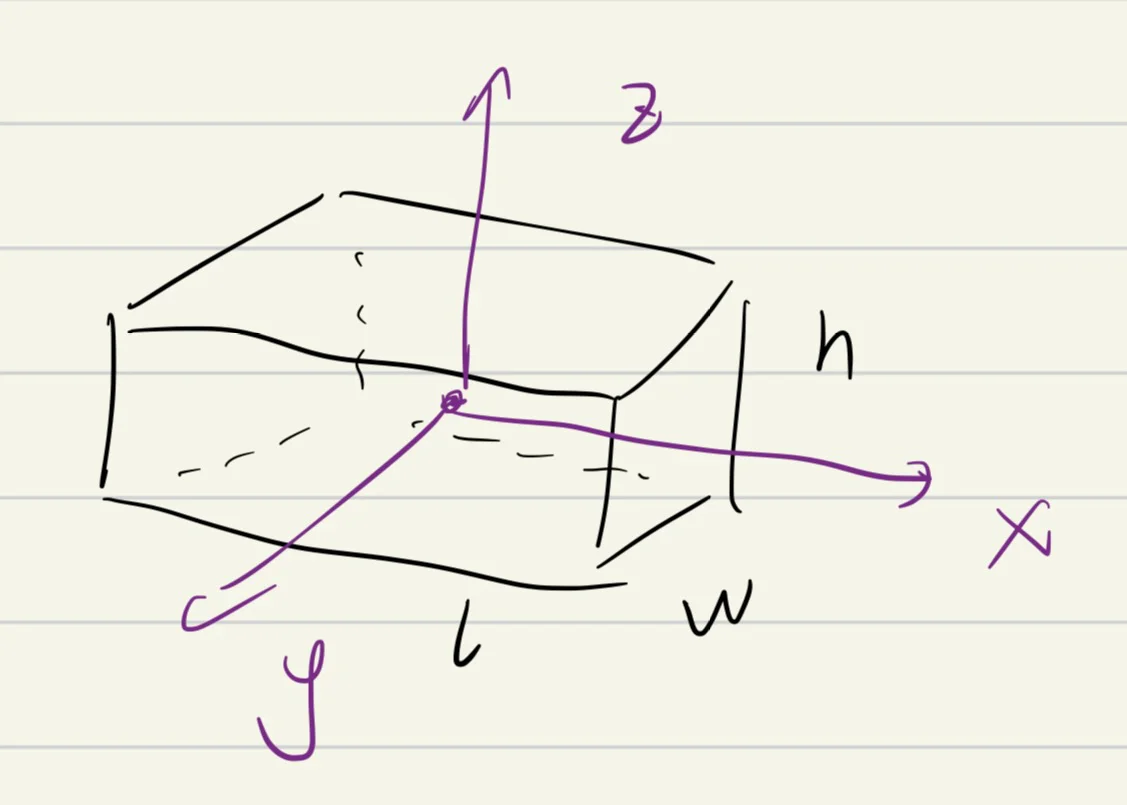
这个题最好自己手推一下，并复习一下多元积分相关的知识

大题 5：两连杆机械臂，一个转动关节一个移动关节，质量集中于末端，标在图上了，求动力学方程

大题 6：长方体工件插入问题

（1）给定任务，把长方体工件插入长方体凹槽，求自然约束和人工约束
（2）-（3）都是阻抗控制相关，没看懂题目

判断题 1：分析雅克比是姿态的最小表示

分析雅可比是基于最小表示推得多

判断题 2：牛顿欧拉法是基于力学的方法，拉格朗日法是基于能量的方法

对，考了多次

判断题 3：一个旋转矩阵对应几个单位四元数

2

判断题 4：关节空间动力学模型的 \(G\) 和笛卡尔空间动力学模型的 \(G_x\) 是否一样

填空题 1：ZYX 欧拉角

旋转矩阵 \(R\) 的左边 6 项已知，求右边 3 项以及 \(\alpha\)、\(\beta\)、\(\gamma\)。利用 \(R\) 和欧拉角转换的公式即可，有一定计算量。

填空题 2：轨迹规划

给了一些条件，需要几次多项式规划；初末用多项式连接，中间用直线规划，有多少解。

填空题 3：惯量积

XY 平面是质量对称平面，哪几个惯量积为 0。

四、（10 分）旋转矩阵计算

右乘联体左乘积。

五、（17 分）R-P 两关节平面机械臂

求末端速度在 0 坐标系的表示，求奇异位形，已知末端 \(f_x\)、\(f_y\)、\(n_z\) 求关节 \(\tau_1\)、\(\tau_2\)（\(l_z\) 是用前面算出的雅克比求的 \(\tau\)，用内推法应该也可以）。

六、（16 分）R-P 两关节机械臂

质量集中，求动力学方程（拉格朗日法即可）；给出 \(\theta\) 和 \(d\) 的期望轨迹 \(y_1(t)\) 和 \(y_2(t)\)，求控制率使得 \(\theta\) 的两个特征根均为 -1，\(d\) 的两个特征根均为 -3，用 \(\alpha\beta\) 分解即可。

七、（17 分）力控制

（1）拧螺丝（和 ppt 不一样，不能沿 Y 轴运动，而且要考虑向下的 Z 速度）写自然约束和人工约束。
（2）讲了什么叫"平行力位控制"，就是力控制和位置控制并非正交，两个控制器的输出要相加。让结合力位混合控制的框图，画出平行力位控制的框图。这个在A4上抄了力位混合的框图就行。
（3）描述完成机器人按下门把推开门的控制策略和控制原理。

八、（10 分）规划姿态

用四元数插补实现。初始 \(q_0\)，结束 \(q_1\)，要求角速度连续，且初末角速度均为 0。这个题没做过类似的，lz 结合了 Slerp 方法并加了两个待定系数，利用 \(q'(t=0)=0\) 和 \(q'(t=1)=0\) 求解出了两个待定系数，但是不知道对不对，这题有点抽象。

判断题 1：单位四元数 \(ab=ba\)

判断题 2：鲁棒控制和自适应控制参数变不变

判断题 3：奇异位形

填空题 1：\(\alpha\)-\(\beta\) 分解

填空题 2：右乘联体左乘基

一、（10 分）正四面体坐标系变换

正四面体三个顶点上画了三个坐标系，求一下三个 \(T\) 矩阵（属于是立体几何题）。

二、（10 分）平面三自由度机械臂逆运动学

平面三自由度机械臂，第一个旋转关节，第二移动关节，第三个旋转关节，求 \(\theta_1\)、\(d_2\)、\(\theta_3\)。

三、（10 分）轨迹规划

起始点 \(0°\)，有个中间点 \(40°\)，终止点 \(70°\)，中间速度连续，起始速度为 0，总时间 1s，两个二次多项式规划。

四、（15 分）三旋转关节机器人

（1）算 0 坐标系下的雅可比矩阵
（2）题目给出具体的角度长度，让算一下各个关节的力矩。

五、（15 分）两自由度机械臂动力学

两自由度机械臂，第一个旋转关节，第二个移动关节，要求用牛顿欧拉法算动力学方程。

六、（15 分）力控制

（1）算了一个自然约束和人工约束
（2）混合力控框图和约束矩阵

一、矩阵计算

给了一个 \(R_{AB}\)，然后 B 绕 K 转 \(\theta\)，再给 \(R_{AB}\)，求 K 和 \(\theta\)。用那个公式算就行，不过当时发现这两个矩阵的第二列相同，就偷懒了。

二、控制设计

设计一个跟踪装置，要求稳定闭环零点。

三、约束分析

一个操作臂，末端擦拭工件，求自然约束和人为约束。

四、动力学分析

考了书上的操作臂 RP 操作臂，不一样的是：关节 1 的 z 轴朝上，关节 2 和关节 1 有个 45° 夹角，从平面运动变成空间运动。用拉格朗日法求解动力学方程。

五、速度传递

一个 2R 连杆，跟书上不一样的是第二个关节转了 90°（有点像竹蜻蜓那样），运动平面跟第一个杆的平面垂直，给了角度和角速度、杆的参数，求末端线速度在基座标系下的速度表示。可以用雅可比矩阵求解。

SCAR 工业机器人有几个滑动关节，几个转动关节？

关于角速度向量哪个说法是错的？

关于 PD 控制哪个说法是错的？

复阻抗是力与什么的比值？

二、欧拉角转换

给定 ZYZ 固定角，求 \(Z'Y'X'\) 欧拉角

三、旋转矩阵

已知 AB 之间旋转关系 1. 求B关于A坐标系下\(\{\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\}\)旋转\(30°\)后两坐标系旋转矩阵 2. 求B关于B坐标系下\(\{\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\}\)旋转\(30°\)后两坐标系旋转矩阵

四、角速度分析

已知两连杆参数，求 \(0\) 坐标系下 \(2\) 坐标系角速度

五、动力学分析

计算运动状态下连杆力，牛顿欧拉法或拉格朗日法那个，考虑重力，形状是横插在墙上的两连杆，第一个关节是移动关节，第二个关节是旋转关节

六、轨迹规划

给定最大加速度和最大速度绝对值，求最小时间从起始角度运动到终止角度的轨迹

七、控制设计

给定两力矩方程，设计线性控制方程（一个 \(Y\) 的矩阵，一个长得像 \(\theta\) 的那个字母）

八、约束分析

拧螺母的自然约束和人为约束

九、坐标变换

给定某 \(U\) 坐标系下 \(A\) 和 \(A'\) 的 \(T\)（位姿矩阵），设计 \(C\) 使 \(A\) 绕 \(C\) 的 \(z\) 轴旋转某角度（未知，也不用算）后再向 \(z\) 轴方向平移一定距离（未知，也不用算）后得到 \(A'\)，求 \(C\) 在 \(U\) 坐标系下的 \(T\)

一、选择题

1. 坐标系 A 和 B 重合，问欧拉参数
2. 在 \(\mathbb{R}^3\) 中的向量外积是不是半群 / 群
3. 问静力传递式中的矩阵和速度雅可比之间的关系
4. 考察惯性张量 I 的相关性质

二、坐标变换

已知 \({}_B^A\!T\) 求 \({}_A^B\!T\)

三、静力分析

已知二连杆（与教材图 3-29 相同）静外力，求关节力矩

四、旋转矩阵

已知一部分 \(R_{Z'Y'X'}\) 的参数，求 R

五、动力学分析

一个 PR 机械臂，求动力学方程

六、控制设计

非线性控制器设计，使得 \(s=-2\pm0.5i\)

七、约束分析

求一个物块的自然约束

八、四元数

单位四元数插补

九、轨迹规划

约束条件下的单自由度机械臂运动规划

一、坐标变换

已知 \({}_A^B\!T\) 矩阵，求 \({}_B^A\!T\) 矩阵

二、旋转矩阵

\(B\) 坐标系先绕自身 \(Z\) 轴旋转 \(30°\)，再绕 \(A\) 坐标系 \(Y\) 轴旋转 \(45°\)，再绕自身 \(X\) 轴旋转 \(60°\)，求 \(R_{AB}\)。并用一组固定角表示出来。

三、运动学分析

二连杆机械臂，已知 \(\{0\}\) 坐标系下末端位置，末端线速度，求解关节角，关节角加速度。

四、静力分析

二连杆机械臂，已知两个关节的力矩，求解末端的作用力。

五、动力学分析

单连杆机械臂，求解动力学方程，用 \(\tau\)、\(\theta\)、\(\dot{\theta}\) 表示。

六、控制设计

二次系统求解控制律，动力学方程是 \(0.05\ddot{\theta} + 0.7\dot{\theta} + \cos(\theta)=\tau\)，要求系统极点为 \(-1\pm2i\)。

七、轨迹规划

用两段三次曲线规划路径，已知起始静止在 \(30°\)，中间点第 \(2\) 秒到达 \(50°\)，最终第 \(4\) 秒停止在 \(90°\)，要求中间点处加速度连续。

八、综合

1. ZMP 有哪三种
2. 已知左脚作用力为 \(20N\)，作用点为 \((1,2)\)，右脚作用力为 \(15N\)，作用点为 \((3,4)\)，求 ZMP
3. Rodrigues 公式如何表示