08 | 力控制 ¶

约 4166 个字预计阅读时间 16 分钟

为了使机械臂以恒定的力在表面上滑动，( 装配、打磨、去毛刺等任务上面 )，需要应用力控制。

todo

力位混合控制，1981，Raibert 和 Craig 提出
阻抗控制，1984，Hogan 提出
导纳控制
关节力 / 力矩控制

Acknowledgement

在写这篇的笔记的时候，参考了下面的文章，感谢作者的分享。

现代机器人学：力学，规划，控制（chapter11 Ⅲ）机器人控制之力控制，混合运动 - 力控制，阻抗控制等 - 知乎

如何形象生动地解释虚功原理、虚位移原理、力之间的关系？ - 知乎

阻抗 / 导纳控制深度解析 _ 阻抗控制和导纳控制 -CSDN 博客

前置知识 ¶

末端力传感器 ¶

关节力矩传感器 ¶

电流环控制：使用关节力矩和电流之间的关系来估计关节力矩：直驱电机 or 减速比较小；内
应变片式

虚功原理 ¶

参考资料如何形象生动地解释虚功原理、虚位移原理、力之间的关系？ - 知乎

之所以叫做虚功，就是这里的力系和位移没有因果关系，任意的平衡力系，任意的可能位移，所以并不是真正的力在位移上做功，只是把力乘以位移写成功的形式，或者你可以理解为一种虚设可能的做功方式。

虚功原理和最小势能原理是从不同角度说明一件事情

形象例子 —— 来自知乎杜老师

引用自如何形象生动地解释虚功原理、虚位移原理、力之间的关系？ - 知乎

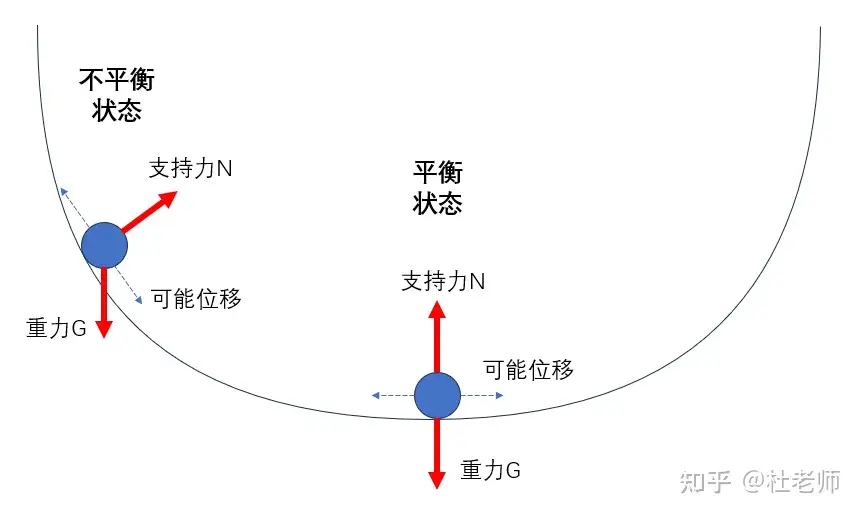
在斜面上，小球受到支持力 N 和重力 G，可能位移可以沿斜面向上或者向下走，这就是虚位移，这两个力在虚位移上做的总虚功不为零，所以是不平衡状态。如果小球向上走，总虚功为负功，如果向下走，总虚功为正功，你可以理解为，功是一种能量转换形式，小球会沿着重力势能降低的方向运动，而总虚功就描述了重力势能的变化趋势。

在碗底水平处，小球受到的支持力 N 和重力 G 都是竖直方向，而虚位移是水平方向，无论向左走还是向右走，总虚功都是 0，所以是平衡状态。你可以理解为，这时候无论小球向左还是向右，它的重力势能变化都是 0，所以它不会动。

从这个角度去看小球的运动，就可以发现它的可能运动方向可能有很多，小球在不同位置的势能是不一样大的，实际总是向着势能更低的方向运动，也就是沿着势能面的最大梯度方向运动。而当小球在某个位置的势能达到了极小值，此处势能面的梯度为零，就会处于平衡状态。这就是常说的最小势能原理

力学第一性原理

力学第一性原理（或力学最高原理），就是可以由他导出全部力学定律的原理或假设。其在力学之中的地位相当于几何学之中的公理。什么原理可以作为力学第一性原理呢？

牛顿运动 3 定律
达朗贝尔原理（又称动力学虚位移原理，或动力学普遍方程）
在静力学情况下是虚位移原理或虚功原理
Lagrange 方程
正则方程
哈密顿原理（这是一种变分原理）

以上原理中的任何一个都可以作为力学的第一性原理，因为它们是相互等价的。

力位混合控制 ¶

几何约束已知，在未约束的任务方向上控制位置，在约束的任务方向上控制力。在不同的方向上被控变量是不同的。

术语解释 ¶

柔性坐标系（约束坐标系 contraint frame）
自然约束（Natural Constraints）：物理环境产生的约束
人工约束（Artificial Constraints）：任务目标决定的约束
按照自然约束 / 人工约束，静力学 / 运动学，可以分成四类：轴方向是正交的，对角方向相同

可行运动空间 (admissible motion space) $V_a \in \mathbb{R}^6$
约束空间 (constraint space) $V_c = V_a ^\bot \in \mathbb{R}^6$

约束求解案例 ¶

柔性坐标系（约束坐标系）的建立比较关键。

如何区分自然约束和人工约束？

假如你是被操作对象，如果在一个方向上，你不能动，那么这个方向就是自然约束。比如轴承在孔中的时候，xy 方向是动不了的，和施加的力无关，因为孔就那么大

梅森规则 ¶

正交性的原因、直观理解

	运动学	静力学
自然约束	$\dot{\vec{p}}_{c}=0$，$\dot{\vec{p}}_{c}\in V_{c}$	$\vec{F}_{a}=0$，$\vec{F}_{a}\in V_{a}$
人工约束	$\dot{\vec{p}}_{a}\in V_{a}$ 可取任意值	$\vec{F}_{c}\in V_{c}$ 可取任意值

根据上面的分析，可以在可行运动空间和约束空间中对静力学和运动学中的自然约束和人工约束进行表征，并且无论约束坐标系各坐标轴是否与控制模态的轴方向对齐，自然约束和人工约束在运动学和静力学上始终具有正交性，且静力学中人工约束对应的子空间与运动学中人工约束对应的子空间也彼此正交。因此，可以在这两个彼此正交的子空间内分别采取位置控制和力控制。

当任务较复杂时，运动空间无法简单地划分为可行运动空间和约束空间。例如，在拧螺钉时，可行运动方向包括了耦合的平移运动与旋转运动，此时利用梅森规则来划分子空间并匹配控制模式就会更加简洁高效。同时，应当注意到实际环境中接触面之间必然会存在摩擦力，环境的刚度也并非无穷大，因此力位混合控制的约束条件通常是对实际问题的简化，这种简化有助于对控制模态的划分。

力位混合控制器 ¶

如果传感器反馈精确无噪声，位置反馈信号应当完全处于可行运动空间，力反馈信号完全处于约束空间当中。

但是实际过程中，传感器会有噪声的影响，所以需要对力和位置进行滤波，把反馈误差投影到位置控制和力控制的子空间当中

轴孔装配任务中的投影矩阵

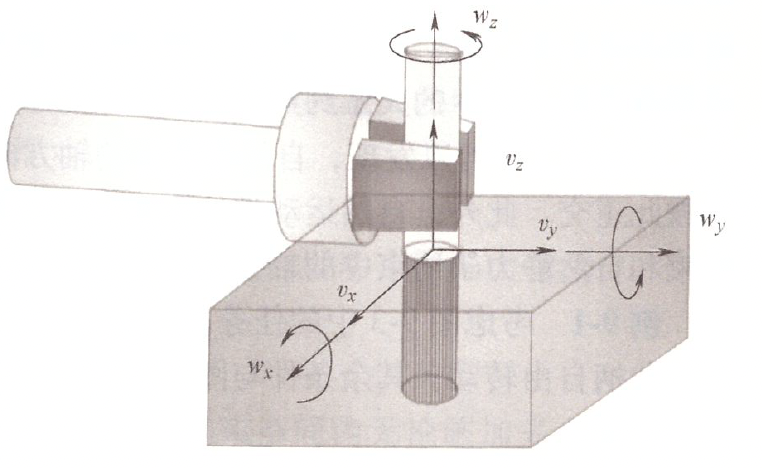
约束类型	运动学约束	静力学约束
自然约束	$v_x = 0$ $v_y = 0$ $\omega_x = 0$ $\omega_y = 0$	$f_z = 0$ $\tau_z = 0$
人工约束	$v_z < 0$ $\omega_z = 0$	$f_x = 0$ $f_y = 0$ $\tau_x = 0$ $\tau_y = 0$

根据前文的分析可知，末端执行器需要在沿 $x$、$y$ 轴平动方向和绕 $x$、 $y$ 轴旋转方向使用力控制，在沿 $z$ 轴平动方向和绕 $z$ 轴旋转方向使用位置控制。因此可将投影矩阵表示为

\[ \boldsymbol{P}_{c}=\mathrm{diag}(1,1,0,1,1,0), \quad \boldsymbol{P}_{a}=\mathrm{diag}(0,0,1,0,0,1) \]

若约束坐标系的各轴与位置和力控制回路中的方向不对齐，投射矩阵就不是对角阵。

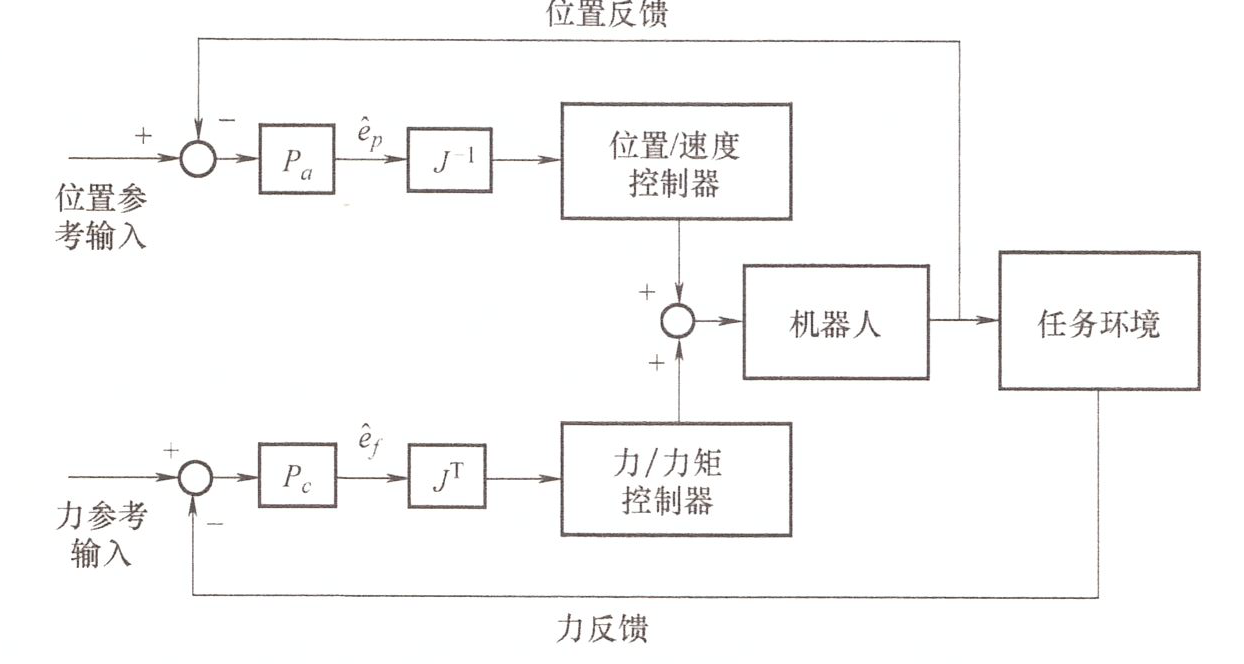
位置误差 $\hat{e}_p$ 和力误差 $\hat{e}_f$ 需要从关节空间转回到笛卡尔空间当中，使用雅可比矩阵 $J$

关节空间的位置误差反馈可表示为 $e_q=J^{-1}\hat{e}_p$
关节空间的力反馈误差可表示为 $e_\tau=J^\mathrm{T}\hat{e}_f$

位置控制器：一般使用 PD 控制器，速度更快
力控制器：PI 控制器，更小稳态误差，噪声强，不适用微分处理

力位混合控制在机器人不对环境做功的时候效果好

为什么不做功的时候控制效果好

阻抗控制 ¶

柔顺控制光看名字就能想象出来了，机械臂正在移动，如果突然来了一个外力，机器人将顺着这个外力运动，外力撤销之后，再回复到之前的状态。就像一个人突然被推了一下，人会产生一个惯性运动，这叫做柔顺。

而 PID 等控制器就是要消除扰动，所以柔顺控制和 PID 控制是相反的。

控制器设计要根据

动力学模型
阻抗模型

形象理解——弹簧门

初始状态：门静止在关闭位置（目标位置）。
外力作用：你推门（导致位置偏移），弹簧门产生反向力抵抗位移。
响应方式：推力越大，门的反作用力越大（刚度），同时门会缓慢复位（阻尼）。
一句话总结：你动它，它推回来（位置决定力）。

机械阻抗：复频域作用力与速度的比值 $\frac{F(s)}{\dot{X(s)}}$

阻抗控制器 ¶

考虑一个简单的一自由度系统：一个质量块与环境进行接触。记质量块的位移为 $x$, 质量为 $m$,$F_{cxt}$ 和 $F$ 分别为环境施加的外力和控制力。质量块的运动方程为

\[ m\ddot{x}=F+F_{ext} \]

若质量块的期望轨迹为 $x_d(t)$, 令 $\widetilde{x}\left(t\right)=x(t)-x_d(t)$ 表示运动的跟踪误差，则阻抗控制的目标可表示为

\[M_d\ddot{\widetilde{x}}+B_d\dot{\widetilde{x}}+K_d\widetilde{x}=F_{ext}\]

式中，$M_d$、$B_d$、$K_d$ 分别表示期望的惯量、阻尼和刚度，三个有一个高叫高阻抗，三个都低叫低阻抗。

\[ F=m\ddot{x}_d+(m-M_d)\ddot{\widetilde{x}}-(B_d\dot{\widetilde{x}}+K_d\widetilde{x}) \]

测量环境力以消除跟踪误差的二阶导数

\[ F=m\ddot{x}_d-\frac{m}{M_d}(B_d\dot{\widetilde{x}}+K_d\widetilde{x})+\left(\frac{m}{M_d}-1\right)F_{ext} \]

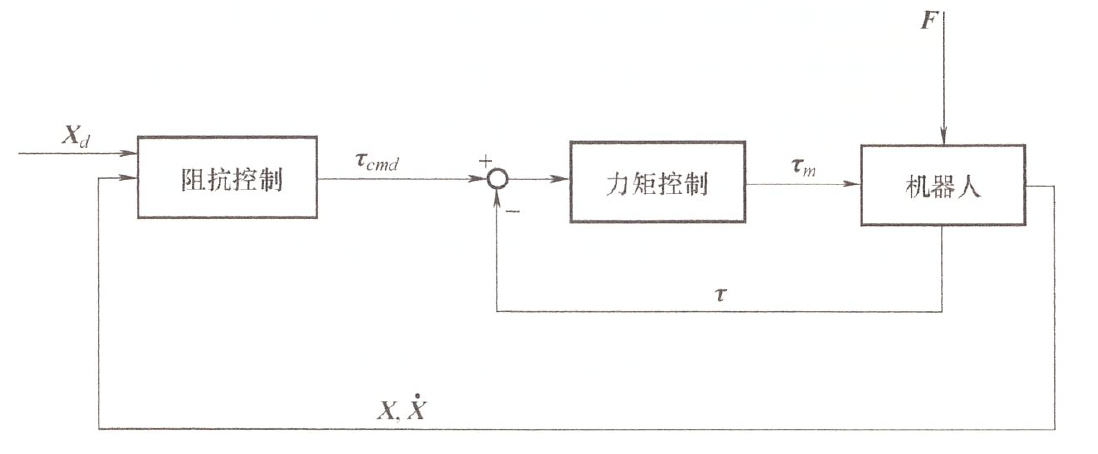
笛卡尔空间阻抗控制 ¶

动力学模型

\[ M(\boldsymbol{\Phi})\ddot{\boldsymbol{\Phi}}+V(\boldsymbol{\Phi},\dot{\boldsymbol{\Phi}})+\boldsymbol{G}(\boldsymbol{\Phi})=\boldsymbol{\tau}+\boldsymbol{J}^\mathrm{T}(\boldsymbol{\Phi})\boldsymbol{F} \]

期望的阻抗关系

\[ \boldsymbol{M}_d\ddot{\widetilde{X}}+\boldsymbol{B}_d\dot{\widetilde{X}}+\boldsymbol{K}_d\widetilde{X}=\boldsymbol{F}_a \]

控制律：

\[ \boldsymbol{\tau}=\boldsymbol{M}(\boldsymbol{\Phi})\boldsymbol{J}_{a}^{-1}(\boldsymbol{\Phi})\left(\ddot{\boldsymbol{X}}_{d}-\dot{\boldsymbol{J}}_{a}(\boldsymbol{\Phi})\dot{\boldsymbol{\Phi}}+\boldsymbol{M}_{d}^{-1}\left(-\boldsymbol{B}_{d}\dot{\widetilde{\boldsymbol{X}}}-\boldsymbol{K}_{d}\tilde{\boldsymbol{X}}\right)\right)+\\V(\boldsymbol{\Phi},\dot{\boldsymbol{\Phi}})+\boldsymbol{G}(\boldsymbol{\Phi})+\boldsymbol{J}_{a}^{\mathrm{T}}(\boldsymbol{\Phi})\left[\boldsymbol{M}_{X}(\boldsymbol{\Phi})\boldsymbol{M}_{d}^{-1}-\boldsymbol{I}\right]\boldsymbol{F}_{a} \]

在阻抗参数矩阵中

$K_d$ 反映末端执行器的刚度大小
- 决定了执行器与环境接触时是呈现刚性还是柔性
- 如果期望轨迹为恒定值，当系统达到稳态时，由于误差的导数都为 $0$，$K_d$ 决定了机器人与环境接触力的大小。
阻尼参数 $B_{t}$ 的变化一般不影响稳态响应，
- 增大 $\boldsymbol{B}_d$，超调减小、响应变慢
惯性参数 $M_d$ 一般不需要进行调节

导纳控制 ¶

控制器接受环境力的输入，改变期望位置

如果环境力太大了，就减小期望位置；如果环境力太小了，就增大期望位置

形象理解——用海绵擦桌子

初始状态：海绵放在桌面上（目标位置）。
外力作用：当你用力按压海绵（外力），海绵会变形（位置改变）。
响应方式：海绵的变形量取决于你的按压力度（外力越大，变形越大），同时海绵内部有弹性（刚度）和阻尼（回弹速度）。
一句话总结：你推它，它动（外力决定位置）。

导纳控制器 ¶

导纳控制的期望位置不是固定的

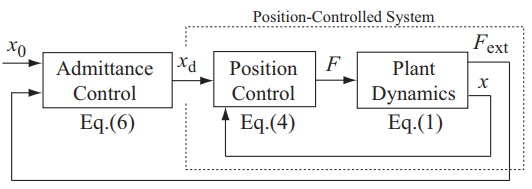
由于质量块还是要由控制力驱动，环路包括一个外环的导纳控制器和一个内环的位置控制器。在导纳控制器中，环境力 $F_\mathrm{ext}$ 通过二阶导纳模型生成一个附加的运动信号，将预期的运动轨迹 $x_d$ 变为新的运动轨迹 $x_m$ $$ M_d(ddot{x}m-ddot{x}_d)+B_ddot{widetilde{x}}+K_dwidetilde{x}=F $$

来计算所需的加速度，求解得到

\[ \ddot{x}_{m}=\ddot{x}_{d}+\frac{1}{M_{d}}(F_{ext}-B_{d}\dot{\widetilde{x}}-K_{d}\widetilde{x}) \]

再对所求得的加速度做两次积分，得到新的运动轨迹并送入位置控制环，来完成最终的控制。

可以发现，当环境力 $F_{ext}=0$ 时有 $(x_m-x_d)\to0$, 只通过位置控制对期望轨迹进行跟踪。

当环境力不为零时，能否实现期望的阻抗关系取决于内环位置控制的精度。

导纳控制器设计 ¶

(1) 输出位置信号，而机器人通常有位置控制模式，故无需建其动力学模型，但要求能测量环境力 (2)需逆运动学，将笛卡尔映射到关节空间 (3)位置控制环增益大，要求刚度(大于环境)和阻尼大 (4)无接触时位置精度高，环境刚度大时可能振荡 (5)属于隐式力控制，期望阻抗关系只保持力位关系，不具体指定接触力，无法跟踪特定力轨迹/直接限制接触力大小

稳态误差 ¶

若要跟踪 F，设接触力误差

\[ F_{e}=F_{r}-F \]

阻抗关系换为

\[ M_{d}\ddot{x}+B_{d}\dot{x}+K_{d}\ddot{x}=F_{e} \]

简化为单一特定方向下参考位置 $x_{d}$ 为定值的恒定接触力任务

\[ m\ddot{x}+b\dot{x}+k(x-x_{d})=e \]

环境建模为弹簧

\[ F=K_{e}(X-X_{e}) \]

得

\[ x=\frac{f}{k_{e}}+x_{e}=\frac{(f_{r}-e)}{k_{e}}+x_{e} \]

代入阻抗关系可得

\[ m\ddot{e}+b\dot{e}+(k+k_{e})e=kf_{r}-k_{e}k(x_{d}-x_{e}) \]

稳态误差

\[ e_{ss}=\frac{k}{k+k_{e}}[f_{r}+k_{e}(x_{e}-x_{d})] \]

取参考位置 $x_{d}=x_{e}+\frac{f_{r}}{k_{e}}$，可使 $e_{ss}=0$

题型 ¶

自然约束 / 人工约束 ¶

案例 1: 轴承装配

约束类型	运动学约束	静力学约束
自然约束	$v_x = 0$ $v_y = 0$ $\omega_x = 0$ $\omega_y = 0$	$f_z = 0$ $\tau_z = 0$
人工约束	$v_z < 0$ $\omega_z = 0$	$f_x = 0$ $f_y = 0$ $\tau_x = 0$ $\tau_y = 0$

案例 2: 旋转曲柄

规定约束坐标系固连在曲柄上并随曲柄运动，x 方向总是指向曲柄的轴心。

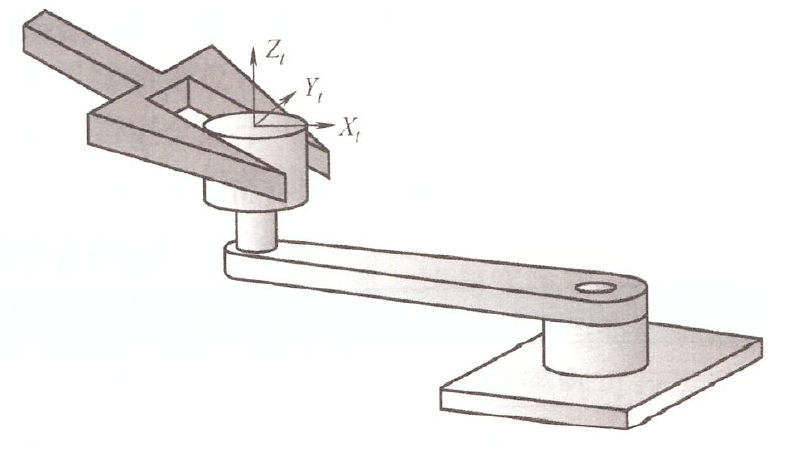
解手柄具有两个自由度，分别为绕 z 轴的转动和绕曲柄轴的转动。约束条件可以整理为下表：

约束类型	运动学约束	静力学约束
自然约束	$v_x = 0$ $v_z = 0$ $\omega_x = 0$ $\omega_y = 0$	$f_y = 0$ $n_z = 0$
人工约束	$v_y = \alpha_1$ $\omega_z = \alpha_2$	$f_x = 0$ $f_z = 0$ $n_x = 0$ $n_y = 0$

其中 $\alpha_1$ 和 $\alpha_2$ 为任意给定的期望速度值。在运动学约束中，自然约束表示机械爪不能在 x 和 z 方向进行平动，也不能绕 x 轴和 y 轴进行旋转；人工约束表示在 y 方向的平动速度和绕 z 轴的转动速度可控。

案例 2: 拧螺丝

拧螺丝任务中物理环境是螺丝表面，轴承装配任务中物理环境是装配孔

约束类型	运动学约束	静力学约束
自然约束	$v_x = 0$ $v_z = 0$ $\omega_x = 0$ $\omega_y = 0$	$f_y = 0$ $n_z = 0$
人工约束	$v_y = 0$ $\omega_z = \alpha_2$	$f_x = 0$ $f_z = \alpha_3$ $n_x = 0$ $n_y = 0$

机器人建模与控制（本）2025-04-07 第 1-2 节

案例 4: 开门

铰链问题、开门、开盒子

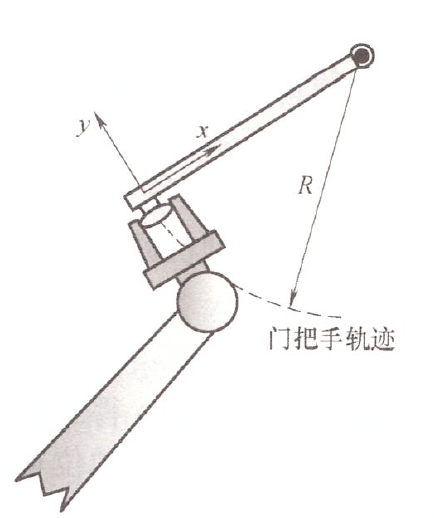
y 方向上给速度，x 方向力恒为 0

约束类型	运动学约束	静力学约束
自然约束	$v_y = 0$ $v_z = 0$ $\omega_x = 0$ $\omega_y = 0$	$f_x = 0$ $n_z = 0$
人工约束	$v_x = a_1$ $\omega_z = \frac{a_1}{r}$	$f_y = 0$ $f_z = 0$ $n_x = 0$ $n_y = 0$

阻抗控制器设计 ¶

根据 $\alpha-\beta$ 律进行分解
设计对应的控制律
列写阻抗控制规律，根据要求的控制目标（极点位置），列写对应的控制律

\[ \boldsymbol{M}_d\ddot{\widetilde{X}}+\boldsymbol{B}_d\dot{\widetilde{X}}+\boldsymbol{K}_d\widetilde{X}=\boldsymbol{F}_a \]

	运动学	静力学
自然约束	\(\dot{\vec{p}}_{c}=0\)，\(\dot{\vec{p}}_{c}\in V_{c}\)	\(\vec{F}_{a}=0\)，\(\vec{F}_{a}\in V_{a}\)
人工约束	\(\dot{\vec{p}}_{a}\in V_{a}\) 可取任意值	\(\vec{F}_{c}\in V_{c}\) 可取任意值

约束类型	运动学约束	静力学约束
自然约束	\(v_x = 0\) \(v_y = 0\) \(\omega_x = 0\) \(\omega_y = 0\)	\(f_z = 0\) \(\tau_z = 0\)
人工约束	\(v_z < 0\) \(\omega_z = 0\)	\(f_x = 0\) \(f_y = 0\) \(\tau_x = 0\) \(\tau_y = 0\)

约束类型	运动学约束	静力学约束
自然约束	\(v_x = 0\) \(v_z = 0\) \(\omega_x = 0\) \(\omega_y = 0\)	\(f_y = 0\) \(n_z = 0\)
人工约束	\(v_y = \alpha_1\) \(\omega_z = \alpha_2\)	\(f_x = 0\) \(f_z = 0\) \(n_x = 0\) \(n_y = 0\)

约束类型	运动学约束	静力学约束
自然约束	\(v_y = 0\) \(v_z = 0\) \(\omega_x = 0\) \(\omega_y = 0\)	\(f_x = 0\) \(n_z = 0\)
人工约束	\(v_x = a_1\) \(\omega_z = \frac{a_1}{r}\)	\(f_y = 0\) \(f_z = 0\) \(n_x = 0\) \(n_y = 0\)