07 | 运动控制 ¶

\(K_p > 0\), 这种控制器被称为比例控制器，或 P 控制器，因为它创建一个与位置误差 \(\theta_e(t) = \theta_d(t) - \theta(t)\) 成比例的校正控制，换句话说，恒定的控制增益 \(K_p\) 有点像一个虚拟的弹簧，试图把实际的关节位置拉到期望的关节位置。P 控制器是线性控制器的一个例子，因为它产生的控制信号是误差 \(\theta_e(t)\) 的线性组合也可能是其的导数和积分。

\(\theta_d(t)\) 是常数 tracking control

如果 \(\theta_d(t)\) 是常数，那么 \(\dot{\theta}_d(t) = 0\)，就称为 setpoint control，这时候误差动力学为：

\[ \dot{\theta}_e(t) = \dot{\theta}_d(t) - \dot{\theta}(t) \]

代入 P 控制器就有：

\[ \dot{\theta}_e(t) = -K_p\theta_e(t) \rightarrow \dot{\theta}_e(t) + K_p\theta_e(t) = 0 \]

如果 \(\theta_{d}(t)\) 不是常数，而 \(\dot{\theta}_{d}(t)=c\)，这时候误差动力学代入 P 控制器为：

\[ \dot{\theta}_{e}(t)=\dot{\theta}_{d}(t)-\dot{\theta}(t)=c-K_{p}\theta_{e}(t) \]

处理一下：

\[ \dot{\theta}_{e}(t)+K_{p}\theta_{e}(t)=c \]

解微分方程，就有：

\[ \theta_{e}(t)=\frac{c}{K_{p}}+\left(\theta_{e}(0)-\frac{c}{K_{p}}\right)e^{-K_{p}t} \]

一阶误差 & PI 控制 ¶

控制律为：

\[ \dot{\theta}(t) = K_p \theta_e(t) + K_i \int_0^t \theta_e(t) \, dt \]

如果 \(\theta_d(t)\) 不是常数，而 \(\dot{\theta}_d(t) = c\)，这时候误差动力学代入 PI 控制器为：

\[ \dot{\theta}_e(t) + K_p \theta_e(t) + K_i \int_0^t \theta_e(t) \, dt = c \]

上式对时间求导：

\[ \ddot{\theta}_e(t) + K_p \dot{\theta}_e(t) + K_i \theta_e(t) = 0 \]

系统的固有频率 \(\omega_n=\sqrt{K_i}\) , 阻尼比 \(\zeta=K_p/2\sqrt{K_i}\)

类比经典的弹簧阻尼系统

增益 \(K_p\) 的作用等同于 \(b/m\) (\(K_p\) 越大，阻尼常数 \(b\) 越大 )
增益 \(K_i\) 的作用等同于 \(k/m\) (\(K_i\) 越大，弹簧刚度 \(k\) 越大 )

那么 \(K_p\) ,\(K_i>0\) 时，PI 控制的误差动力学方程是稳定的，特征方程的根为：

\[ s_{1,2}=-\frac{K_p}{2}\pm\sqrt{\frac{K_p^2}{4}-K_i} \]

PI 反馈 + 前馈 ¶

反馈控制的一个缺点是在关节开始运动之前需要有一个误差，在任何误差累积之前，最好利用我们对所需轨迹的了解来启动运动。我们可以将前馈控制在没有误差的情况下也能控制运动的优点与反馈控制限制误差积累的优点相结合，就有：

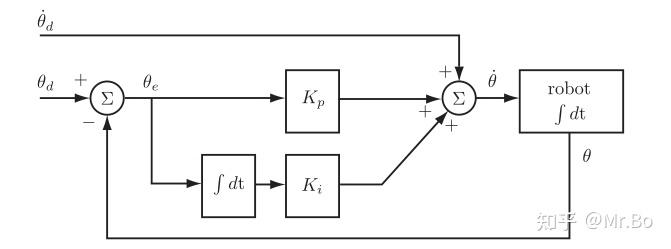
\[\ \dot{\theta}(t)=\dot{\theta}_d(t)+K_p\theta_e(t)+K_i\int_0^t\theta_e(t)\:dt \]

图片来自知乎 Mr.bo

关节建模 ¶

这里有很多字母，联系英文进行记忆

电机建模 ¶

符号	描述	英文翻译
\(T_{ei}\)	电机转矩	Motor torque
\(C_{Ti}\)	转矩系数	Torque coefficient
\(I_{mi}\)	电机的电流	Motor current
\(E_{mi}\)	电机的电动势	Motor voltage
\(\omega_{mi}\)	电机的转速	Motor speed
\(k_{ei}\)	电机的反电动势常数	Back EMF constant
\(R_{mi}\)	电机的电阻	Motor resistance
\(U_{mi}\)	电机的电压	Motor voltage
\(k_{ui}\)	关节 \(i\) 电机驱动器的增益；节省能量，用小功率的器件控制大功率的电机	Joint \(i\) motor driver gain

带驱动器的直流有刷电机模型：转矩 & 转速

\[ T_{ei} = C_{ti} \cdot I_{mi} \]

\[ \omega_{mi} = (\frac{k_{ui}}{k_{ei}})U_{ci} - (\frac{R_{mi}}{k_{ei}})I_{mi} \]

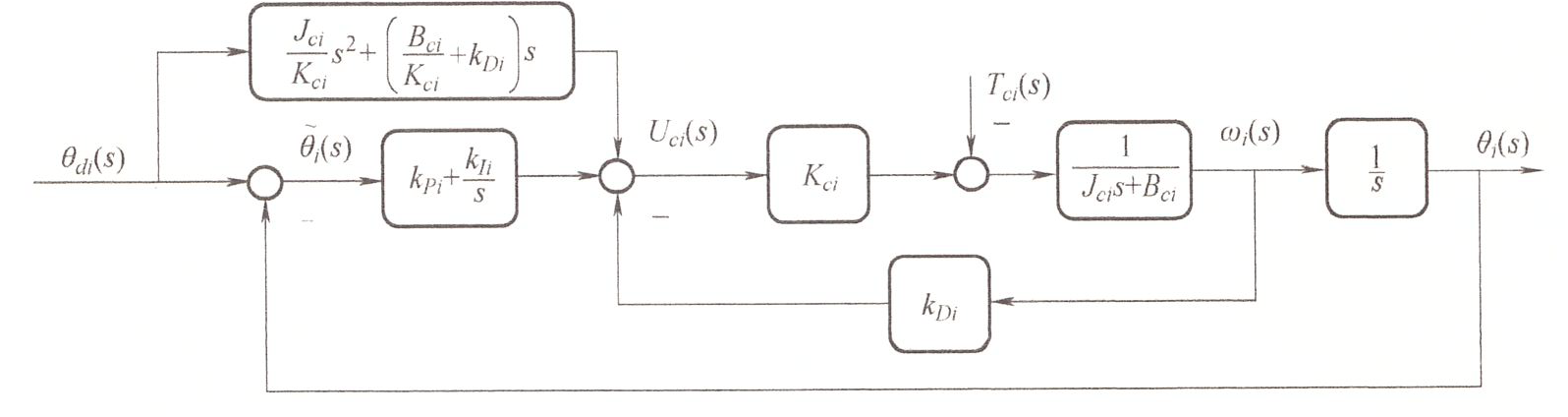
关节建模与传递函数 ¶

\(\theta_{mi}\) 电机转角 \(\theta_{i}\) 关节i转角 \(T_{ei}\) 电机的输出力矩 \(T_{ai}\) 输入齿轮对关节的作用力矩 \(T_{li}\) 反作用力的力矩，后续方程可以约掉 \(T_{ci}\) 干扰力矩 \(b_{mi},b_{ai}\) 轴承的粘性摩擦系数 \(J\) 转动惯量

减速器：其实是扭矩放大器，代价是转速的下降

编码器：对转速进行观测

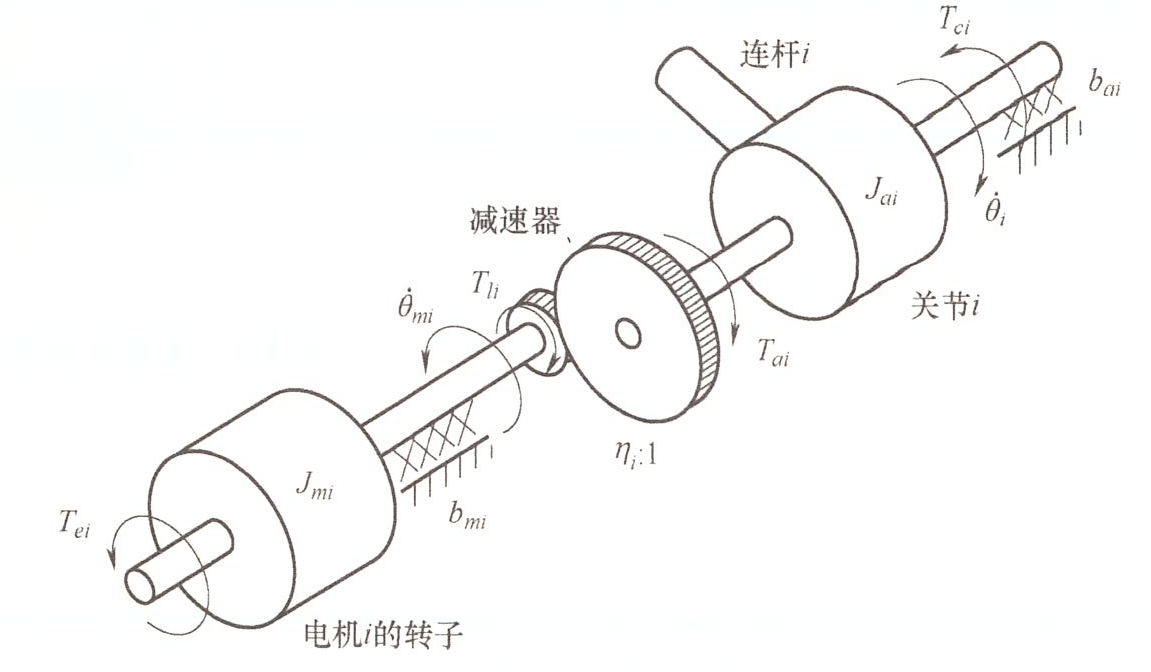
电机动力学：\(J_{mi}\dot{\omega}_{mi}=T_{ei}-T_{li}-b_{mi}\omega_{mi}\)

关节侧动力学： \(J_{ai}\dot{\omega}_{i}=T_{ai}-T_{ci}-b_{ai}\omega_{i}\)

转速关系：\(\omega_i = \frac{\omega_{mi}}{\eta_i}\)，转速下降，扭矩上升

使用 \(\eta * eq1 + eq2\) 可以得到关节模型

\(J_{ci}\ddot{\theta}_{i}+B_{ci}\dot{\theta}_{i}=J_{ci}\dot{\omega}_{i}+B_{ci}\omega_{i}=K_{ci}U_{ci}-T_{ci}\)

输入量：\(U_{ci}\)
干扰输入 \(T_{ci}\)
输出 \(\theta_i\)

关节传递模型框图

Laplace 变换

\[ J_{ci}s^2\theta_i(s)+B_{ci}s\theta_i(s)=K_{ci}U_{ci}(s)-T_{ci}(s) \]

得到系统的传递函数

\[ \theta_i(s)=\frac{K_{ci}}{s(J_{ci}s+B_{ci})}U_{ci}(s)-\frac{1}{s(J_{ci}s+B_{ci})}T_{ci}(s) \]

多关节：独立关节控制 ¶

阶跃输入 | PD 控制器 - 有静差 ¶

反馈信号是：被控对象的输出 \(\theta_i\) 和其微分

控制算法：

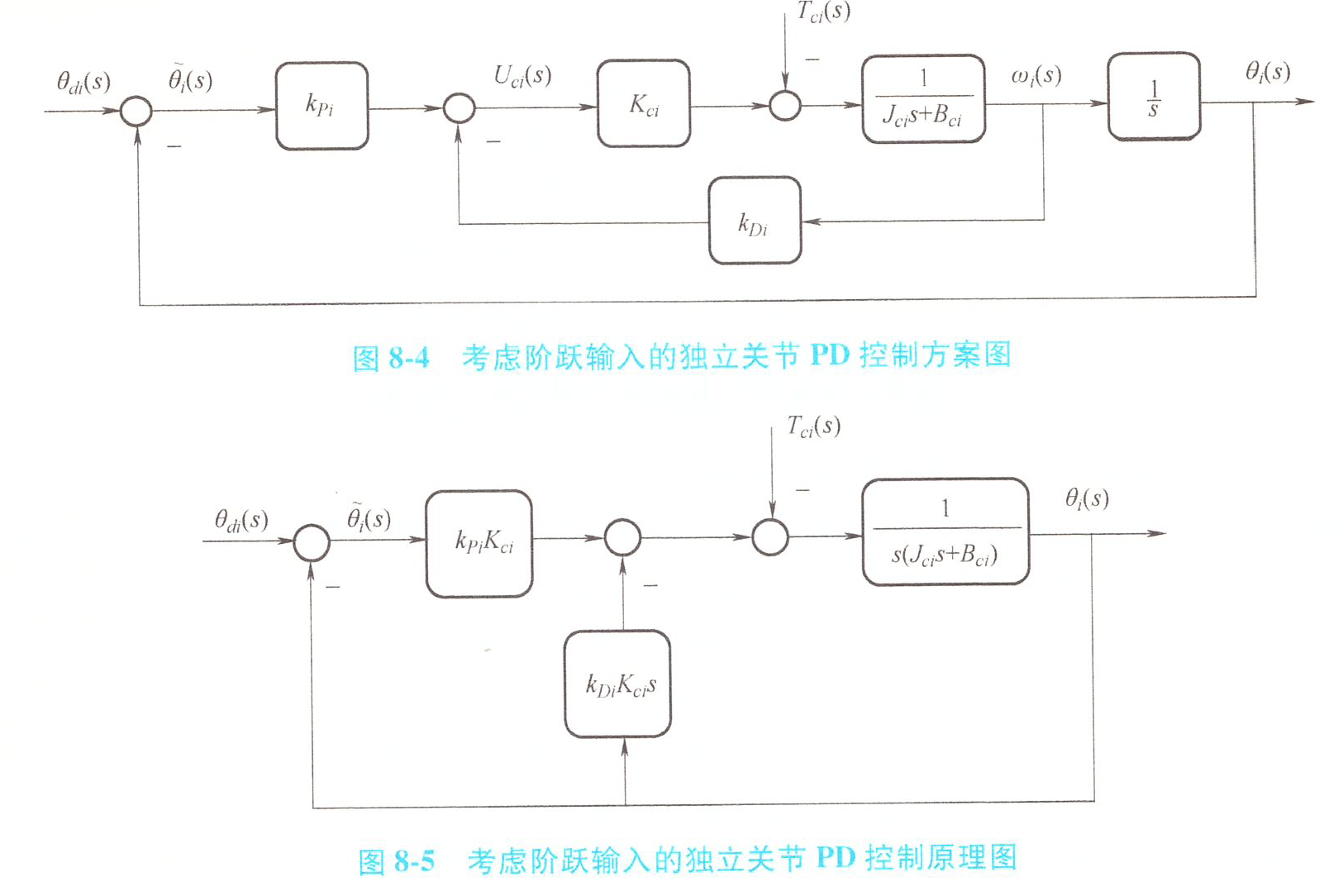
\[ \begin{align*} U_{ci}(s) = k_{P_i}\widetilde{\theta}_i(s) - k_{D_i}\omega_i(s)\\ \widetilde{\theta}_i(s) = \theta_{di}(s) - \theta_i(s) \end{align*} \]

\[ \theta_{i}(s)=\frac{k_{Pi}K_{ci}}{J_{ci}s^{2}+(B_{ci}+k_{Di}K_{ci})s+k_{Pi}K_{ci}}\theta_{di}(s)-\frac{1}{J_{ci}s^{2}+(B_{ci}+k_{Di}K_{ci})s+k_{Pi}K_{ci}}T_{ci}(s) \]

稳定性分析 ¶

这里需要用到二阶动态性能的一些公式以及稳定性分析中的劳斯判据知识

闭环特征多项式为

\[ s^{2}+\frac{B_{ci}+k_{Di}K_{ci}}{J_{ci}}s+\frac{k_{Pi}K_{ci}}{J_{ci}} \]

阻尼比 \(\zeta=\frac{B_{ci}+k_{Di}K_{ci}}{2\sqrt{J_{ci}k_{pi}K_{ci}}}\)
- 当 \(0<\zeta<1\) 时，式 (8-21) 成为欠阻尼系统，有一对共轭复数根为
\[ s_{1,2}=-\zeta\omega_{0}\pm\mathrm{j}\omega_{0}\sqrt{1-\zeta^{2}} \]
- 当 \(\zeta>1\) 时 , 为过阻尼系统，其闭环特征方程有两个相异实数根为
\[ s_{1,2}=-\zeta\omega_{0}\pm\omega_{0}\sqrt{\zeta^{2}-1} \]
- 设计的时候通常选择 \(\zeta=1\)，即临界阻尼系统，这样系统响应最快

自然频率 \(\omega_{0}=\sqrt{\frac{k_{pi}K_{ci}}{J_{ci}}}\)
- \(\omega_0\) 根据控制电压上限和快速性之间进行折中

误差传递函数

\[ \tilde{\theta}_i\left(s\right)= \theta_{di}\left(s\right) - \theta_i\left(s\right) \]

\[ \lim_{t\to+\infty}\widetilde{\theta}_{i}(t)=\lim_{s\to0}s\frac{1}{J_{ci}s^{2}+(B_{ci}+k_{Di}K_{ci})s+k_{Pi}K_{ci}}\frac{1}{s}=\frac{1}{k_{Pi}K_{ci}} \]

无扰动的情况下无静差，阶跃信号的时候有扰动的影响，比例控制 \(k_{pi}\) 越大，扰动的影响越小

这里化简的时候使用梅森增益公式求解比较简单

阶跃输入 | PID 控制器 - 消除静差 ¶

带一个积分环节

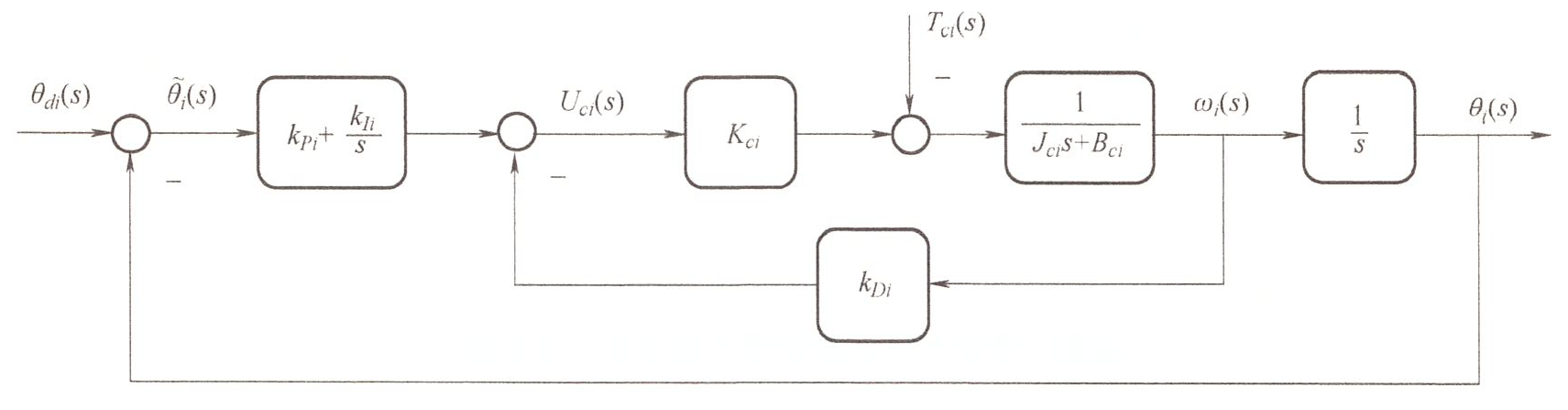
阶跃扰动下，独立关节 PID 可以做到无静差

二阶可导输入｜前馈 PID ¶

阶跃输入的信号，通常用于点对点的移动，但是对于一般的轨迹规划任务，都是二阶可导的（如五次多项式轨迹）

前馈的引入不改变稳定性和闭环极点

消除参考输入影响

转矩前馈控制 ¶

对关节干扰进行推算，增加补偿量主动消减干扰的影响

这里书上的公式有点复杂

多关节：集中控制 ¶

可以看出教材是一步步逐渐递进的，各个方法需要准确获取的参数越来越少，鲁棒性越来越强

\[ \eta_iT_{ei}=\eta_iC_{Ti}V_{ci}-\eta_i^2\frac{C_{Ti}k_{ei}}{k_{ui}\pi_{pi}+R_{mi}}\dot{\theta}_i \]

\(\eta_i T_{e i}\) 是第 \(i\) 个关节电机（含减速器）对机器人的驱动转矩。记

\(\tau = \begin{pmatrix} \eta_1 T_{e 1} \\ \vdots \\ \eta_N T_{e N} \end{pmatrix}, \tau_d = \begin{pmatrix} \eta_1 C_{T 1} V_{c 1} \\ \vdots \\ \eta_N C_{T N} V_{c N} \end{pmatrix}, B_e = \begin{pmatrix} \eta_1^2 \frac{C_{T 1} k_{e 1}}{k_{u 1} \pi_{p 1} + R_{m 1}} & \cdots & \eta_N^2 \frac{C_{T N} k_{e N}}{k_{u N} \pi_{p N} + R_{m N}} \end{pmatrix}, \dot{\Phi} = \begin{pmatrix} \dot{\theta}_1 \\ \vdots \\ \dot{\theta}_N \end{pmatrix}\)

则对于全部关节电机，有 \(\tau = \tau_d - B_e \dot{\Phi}\)

与机器人动力学方程式合并，得到集中控制的被控对象模型

\[ M(\Phi) \ddot{\Phi} + C(\Phi, \dot{\Phi}) \dot{\Phi} + L \dot{\Phi} + G(\Phi) = \tau_d \]

式中，\(L = B + B_e\) 为正定对角矩阵。

集中控制的任务在于设计计算 \(\tau_d\) （相当于计算各关节电机期望电流）的算法，使得 \(\Phi\) 跟踪 \(\Phi_d\)。

重力补偿 PD 控制 ¶

重力力矩在控制中往往被视为一种非线性扰动，但是重力矩的数学模型可获取，因此，可作为一种已知的非线性扰动。直接补偿掉，在推导控制算法时就不需要考虑重力项了。

在实验中，重力补偿的明显作用有两点：1. 在位置控制时，能够增加机器人的动态性能，动态跟踪误差相比无重力补偿时更小。在无积分的位置控制器中，如 PD 控制器，重力补偿能够减少稳态误差。

控制律为

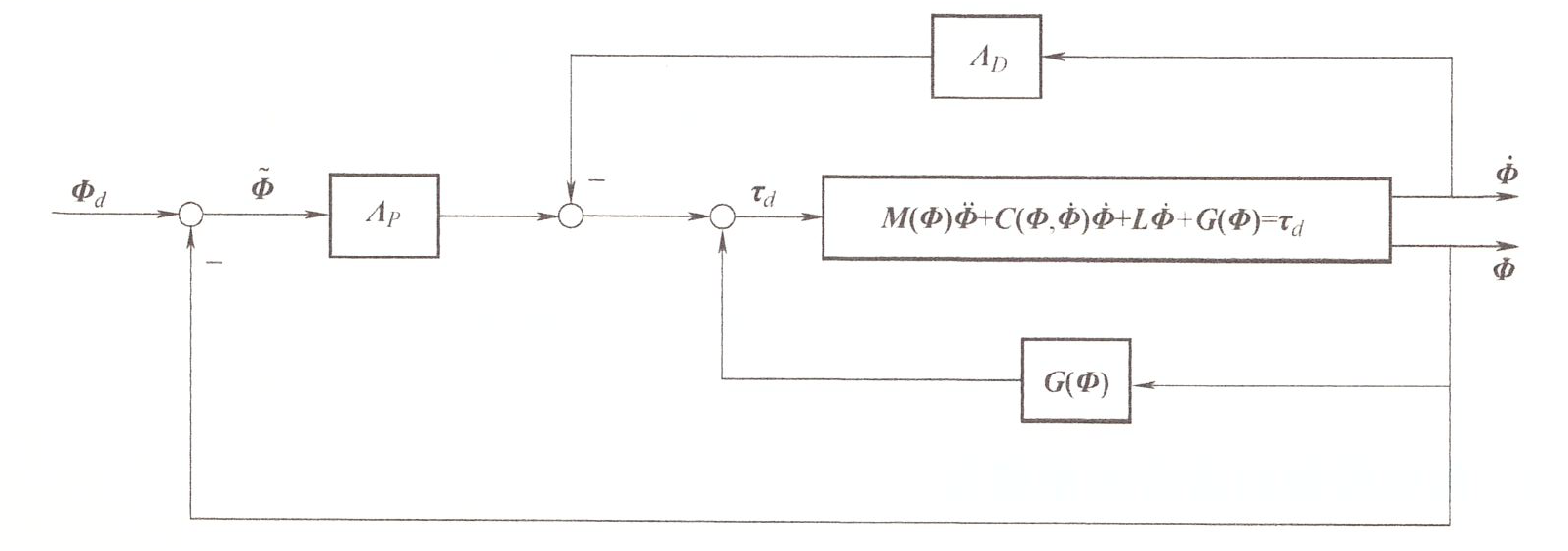
\[ \boldsymbol{\tau}_d=\boldsymbol{\Lambda}_P(\boldsymbol{\Phi}_d-\boldsymbol{\Phi})-\boldsymbol{\Lambda}_D\dot{\boldsymbol{\Phi}}+\boldsymbol{G}(\boldsymbol{\Phi}) \]

Lyapunov 方法证明收敛

\[ M\ddot{\Phi}=\Lambda_P\widetilde{\Phi}-(C+L+\Lambda_D)\dot{\Phi} \]

取 \((\widetilde{\Phi}^T,\dot{\Phi}^T)^T\) 为该闭环系统的状态，则其状态方程为

\[ \begin{pmatrix}\dot{\Phi}\\\ddot{\Phi}\end{pmatrix}=\begin{pmatrix}0&-I\\M^{-1}\Lambda_P&-M^{-1}(C+L+\Lambda_D)\end{pmatrix}\begin{pmatrix}\widetilde{\Phi}\\\dot{\Phi}\end{pmatrix} \]

表明这是一个自治系统且原点是系统的平衡状态。构造正定李亚普诺夫函数

\[ V_L(\widetilde{\Phi},\dot{\Phi})=\frac{1}{2}\dot{\Phi}^TM\dot{\Phi}+\frac{1}{2}\widetilde{\Phi}^T\Lambda_P\widetilde{\Phi} \]

那么

\[ \begin{align*} \dot{V}_L(\widetilde{\Phi},\dot{\Phi})&=\dot{\Phi}^TM\ddot{\Phi}+\frac{1}{2}\dot{\Phi}^TM\dot{\Phi}+\dot{\widetilde{\Phi}}^T\Lambda_P\widetilde{\Phi}\\ &=\dot{\Phi}^T(\Lambda_P\widetilde{\Phi}-(C+L+\Lambda_D)\dot{\Phi})+\frac{1}{2}\dot{\Phi}^TM\dot{\Phi}-\dot{\Phi}^T\Lambda_P\widetilde{\Phi}\\ &=\frac{1}{2}\dot{\Phi}^T(M-2C)\dot{\Phi}-\dot{\Phi}^T(L+\Lambda_D)\dot{\Phi} \end{align*} \]

注意到 \(\dot{M}-2C\) 的反对称性使得 \(\dot{\Phi}^T(\dot{M}-2C)\dot{\Phi}=0\)，于是

\[ \dot{V}_L(\widetilde{\Phi},\dot{\Phi})=-\dot{\Phi}^T(L+\Lambda_D)\dot{\Phi} \]

这意味着 \(\dot{V}_L(\widetilde{\Phi},\dot{\Phi})\) 半负定（\(\dot{V}_L(\widetilde{\Phi},\dot{\Phi})=0\) 时，\(\widetilde{\Phi}\) 可以非零）。接下来，需要证明 \(\dot{V}_L(\widetilde{\Phi},\dot{\Phi})\)

自治系统与非自治系统

来源：什么是自治系统、非自治系统、时不变系统、时变系统？ - 知乎

考虑如下系统：

\[ \dot{x} = f(t, x) \]

其中 \(x = [x_1, x_2, \ldots, x_n]^T \in \mathbb{R}^n\) 是系统状态，\(t > 0\) 是时间。

\(f(t, x)\) 中显含时间 \(t\) 的系统就是非自治系统（nonautonomous system），也称时变系统（time varying system）。

如果不显含时间 \(t\)，即

\[ \dot{x} = f(x) \]

称为自治系统（autonomous system），也称为时不变系统（time invariant system）。

注 1：决定自治和非自治的是是否“显含时间 \(t\)”。注意这里的描述是“显含”而不是“不含”。事实上，\(x\) 本身就是时间的函数，即 \(x = x(t)\)，也就是说系统 (1) 的完整描述是 \(\dot{x}(t) = f(t, x(t))\)，系统 (2) 的完整描述是 \(\dot{x}(t) = f(x(t))\)。\(x(\cdot)\) 中包含的时间 \(t\) 对于系统来说不是显含的，而是隐含的，所以 \(x(\cdot)\) 中所包含的时间 \(t\) 与判断系统是否自治无关。

注 2：如果 \(f\) 是线性的，那么系统 (1) 就是线性非自治系统（线性时变系统），系统 (2) 就是线性自治系统（线性时不变系统）。

反对称矩阵二次型为 0

标量的转置是本身

如果 \(A\) 是反对称矩阵，即 \(A^T = -A\)，则对于任意向量 \(x\)，有 \(x^T A x = 0\)。这显然成立，因为：

\[ x^T A x = x^T (-A^T) x = -x^T A^T x = -(x^T A x)^T = -x^T A x \]

所以 \(2x^T A x = 0\)，即 \(x^T A x = 0\)。

不恒为零：从任意非零初态（\(\widetilde{\Phi}^{T}(0)\) \(\dot{\Phi}^{T}(0)\)）\(^{T}\) 出发的解（\(\widetilde{\Phi}^{T}(t)\) \(\dot{\Phi}^{T}(t)\)）\(^{T}\) 不会有 \(\dot{V}_{L}(\widetilde{\Phi}(t), \dot{\Phi}(t)) \equiv 0\)。

采用反证法，假设从某非零初态（\(\widetilde{\Phi}^{T}(0)\) \(\dot{\Phi}^{T}(0)\)）\(^{T}\) 出发的解（\(\widetilde{\Phi}^{T}(t)\) \(\dot{\Phi}^{T}(t)\)）\(^{T}\) 有 \(\dot{V}_{L}(\widetilde{\Phi}(t), \dot{\Phi}(t)) \equiv 0\)，即 \(-\dot{\Phi}^{T}(t)(L + \Lambda_{D})\dot{\Phi}(t) \equiv 0\)。显然 \(\dot{\Phi}(t) \equiv 0\)，其导函数 \(\ddot{\Phi}(t) \equiv 0\)，进而由式（8-83）知 \(\ddot{\Phi}(t) \equiv 0\)。于是（\(\widetilde{\Phi}^{T}(t)\) \(\dot{\Phi}^{T}(t)\)）\(^{T} \equiv 0\)，则初态（\(\widetilde{\Phi}^{T}(0)\) \(\dot{\Phi}^{T}(0)\)）\(^{T} = 0\)，这与非零初态假设矛盾，“不恒为零”得证。最后，当 \(\|[\widetilde{\Phi}^{T} \quad \dot{\Phi}^{T}]^{T}\| \rightarrow \infty\) 时，有 \(V_{L}(\widetilde{\Phi}, \dot{\Phi}) \rightarrow \infty\)。

综上，系统式的原点平衡状态是大范围渐近稳定的。因此，对任意初态（\(\widetilde{\Phi}^{T}(0)\) \(\dot{\Phi}^{T}(0)\)）\(^{T}\)，有

\[ \lim_{{t \to +\infty}} (\widetilde{\Phi}^{T}(t) \quad \dot{\Phi}^{T}(t))^{T} = 0 \]

重力补偿 PD 控制可以使 \(\Phi\) 收敛于定常的 \(\Phi_d\)，适用于一种静止位形运动到另一种静止位形

feedback linearization¶

这一块可以看机器人学 -4-3- 线性控制 - 知乎这个博主的笔记，讲的很好

旨在把控制律分解为一个包含单位质量系统的部分 ( 可以通过设置变量达到临界阻尼 ) 和除了单位质量系统之外的所有和机器人物理相关的部分。

定义

\[ f := \alpha f' + \beta \]

\(\alpha\) 和 \(\beta\) 称为基于模型的控制部分 (model-based portion);
\(f'\) 称为伺服控制部分 (servo portion)

PD 控制律

\[ f' = -k_v \dot{x} - k_p x \]

伺服控制律

\[ f' = \ddot{x_d} + k_v \dot{e} + k_p e \]

其中 \(e = x_d - x\)。这样连立之后，会得到

\[ \begin{align*} m \ddot{x} + b \dot{x} + kx &= \alpha f' + \beta\\ m \ddot{x} + b \dot{x} + kx &= \alpha (\ddot{x_d} + k_v \dot{e} + k_p e) + \beta\\ \ddot{x} &= \ddot{x_d} + k_v \dot{e} + k_p e\\ \ddot{e} + k_v \dot{e} + k_p e &= 0 \end{align*} \]

例子 1 —— 机器人动力学例子 2

\[ M(q)\ddot{q}+C(q)[\dot{q}^{2}]+B(q)[\dot{q}\dot{q}]+G(q)=\tau= \alpha\tau^{\prime}+\beta\]

其中 :

\[ \begin{align*} \alpha&=M(q)\\ \beta&=C(q)[\dot{q}^{2}]+B(q)[\dot{q}\dot{q}]+G(q)\\ \tau^{\prime}&=\ddot{q} \end{align*} \]

without robot dynamics:

\[ \tau^{\prime}=\ddot{q}_{d}+k_{v}\dot{e}+k_{p}e \]

图片来自机器人学 -4-3- 线性控制 - 知乎

\[ m \ddot{x} + b \dot{x} + kx = f \]

\[ m \ddot{x} + b \dot{x} + kx = \alpha f' + \beta \]

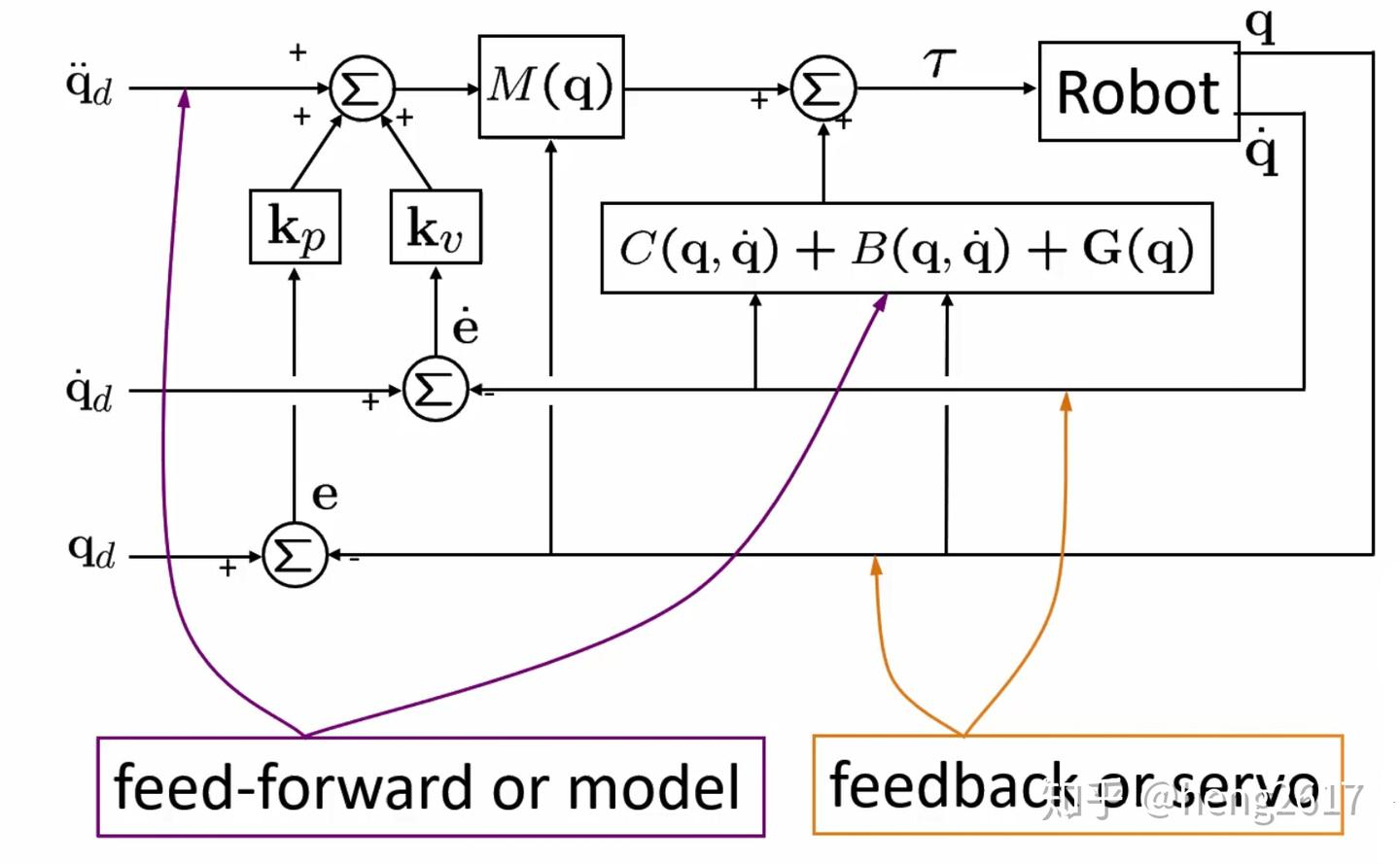
令： \(\alpha := m\) ， \(\beta := b \dot{x} + kx\) 有：

\[ \ddot{x} = f' \]

就变成了一个单位质量系统的运动方程

什么是伺服

（1）伺服系统：是使物体的位置、方位、状态等输出，能够跟随输入量（或给定值）的任意变化而变化的自动控制系统。

（2）在自动控制系统中，能够以一定的准确度响应控制信号的系统称为随动系统，亦称伺服系统。

伺服的主要任务是按控制命令的要求，对功率进行放大、变换与调控等处理，使驱动装置输出的力矩、速度和位置控制得非常灵活方便。

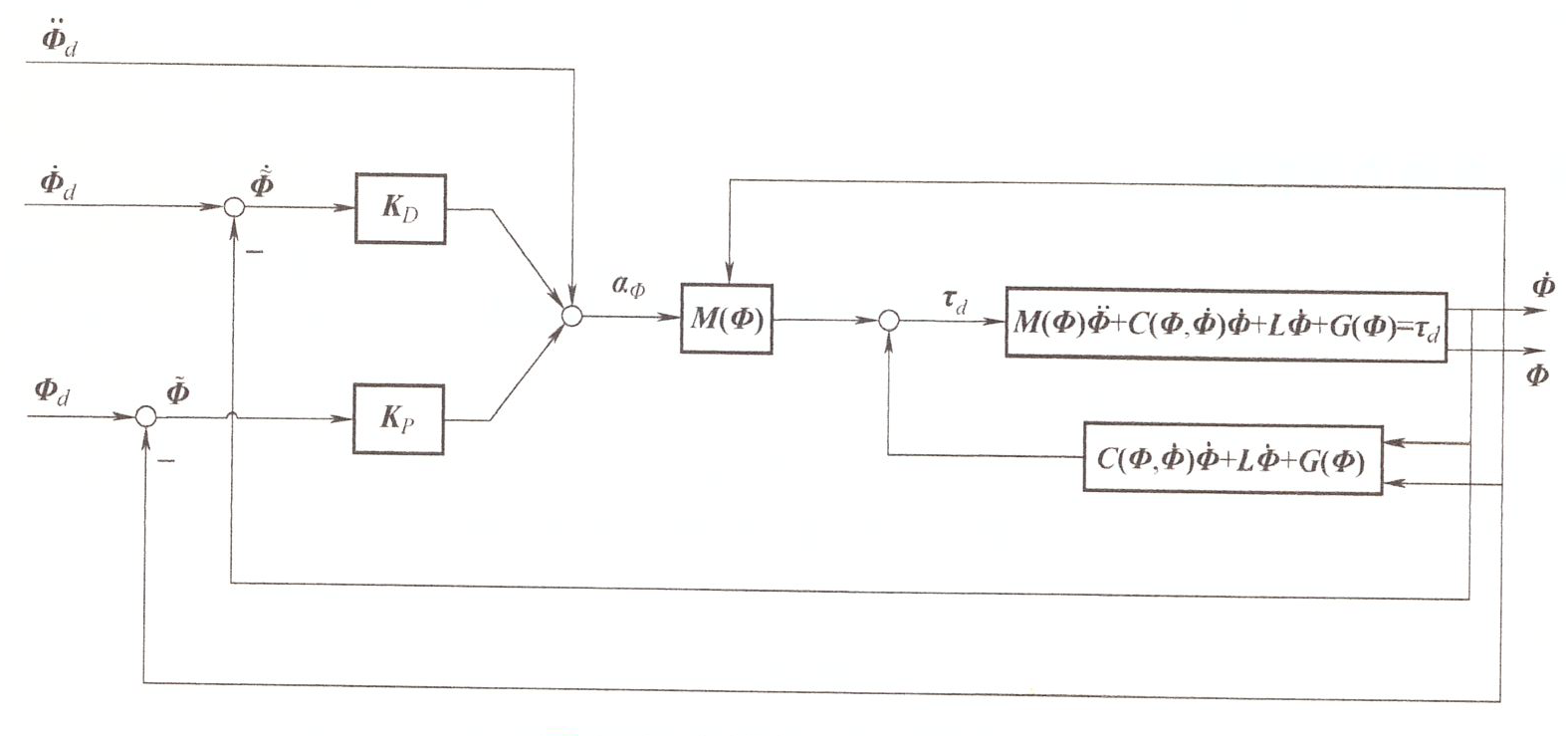
逆运动学控制 ¶

什么是逆运动学控制？

直接根据期望的关节位移，计算出关节位置，然后使用 PD 控制器，把关节控制在想要的位置上面。

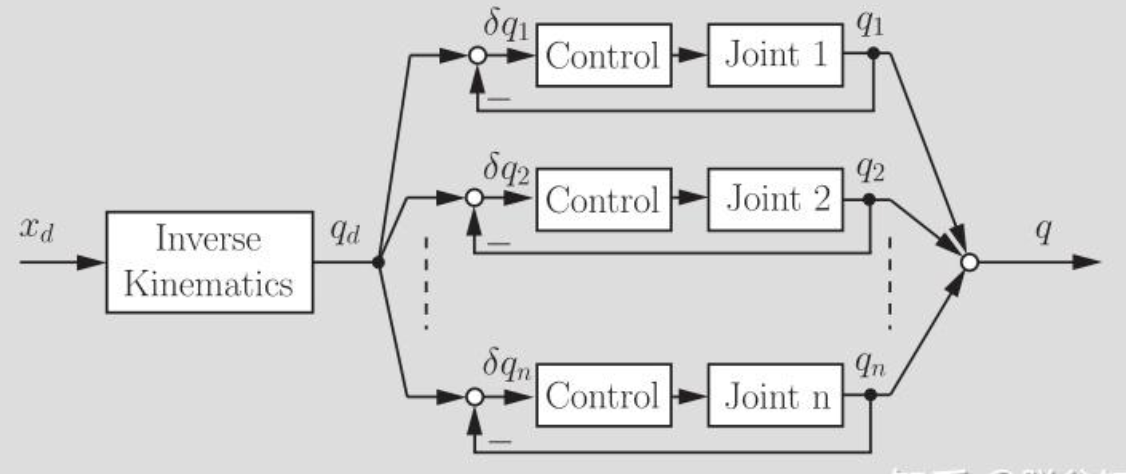
在反馈中利用补偿将复杂非线性模型化成 N 个无耦合的单变量的线性模型

采用补偿：

\[ \boldsymbol{\tau}_d=\boldsymbol{M}(\boldsymbol{\Phi})\boldsymbol{\alpha}_\phi+\boldsymbol{C}(\boldsymbol{\Phi},\dot{\boldsymbol{\Phi}})\dot{\boldsymbol{\Phi}}+\boldsymbol{L}\dot{\boldsymbol{\Phi}}+\boldsymbol{G}(\boldsymbol{\Phi}) \]

这里采用了 \(\alpha-\beta\) 分解的思想

得到：

\[ \ddot{\Phi} = \alpha_\Phi \]

这样就变成了 N 个线性的双积分系统，可以使用带前馈的 PD 控制器等等

所以控制律为

\[ \alpha_{\phi}=\ddot{\boldsymbol{\Phi}}_{d}+K_{D}\dot{\widetilde{\boldsymbol{\Phi}}}+K_{P}\widetilde{\boldsymbol{\Phi}} \]

其中，\(\ddot{\boldsymbol{\Phi}}_{d}+K_{D}\dot{\widetilde{\boldsymbol{\Phi}}}\) 是前馈的部分 , 即框图左上角的部分

鲁棒控制｜估计参数 ¶

\(M(\boldsymbol{\Phi})\ddot{\boldsymbol{\Phi}}+C(\boldsymbol{\Phi},\dot{\boldsymbol{\Phi}})\dot{\boldsymbol{\Phi}}+L\dot{\boldsymbol{\Phi}}+G(\boldsymbol{\Phi})=\boldsymbol{\tau}_d\) 的参数值无法准确获取，使用估计值进行控制

控制律

\[ \boldsymbol{\alpha}_{\phi}=\ddot{\boldsymbol{\Phi}}_{d}+\boldsymbol{K}_{D}\dot{\widetilde{\boldsymbol{\Phi}}}+\boldsymbol{K}_{P}\widetilde{\boldsymbol{\Phi}}+\boldsymbol{\Xi} \]

其中，\(\boldsymbol{\Xi}\) 是不确定性项

\[ \boldsymbol{\Xi}=\boldsymbol{B}_r(\boldsymbol{\varphi})=\begin{cases}(\rho_1+\rho_2\|\boldsymbol{\varphi}\|)\frac{\overline{B}^\mathrm{T}\boldsymbol{P}_L\boldsymbol{\varphi}}{\|\overline{B}^\mathrm{T}\boldsymbol{P}_L\boldsymbol{\varphi}\|},&\text{当}\|\overline{\boldsymbol{B}}^\mathrm{T}\boldsymbol{P}_L\boldsymbol{\varphi}\|\neq0\text{时}\\\\0,&\text{当}\|\overline{\boldsymbol{B}}^\mathrm{T}\boldsymbol{P}_L\boldsymbol{\varphi}\|=0\text{时}&\end{cases} \]

一些参数的定义如下

\[ \begin{align*} &\rho_{1}>\frac{1}{1-\gamma_{3}}(\gamma_{3}\gamma_{2}+\overline{m}\gamma_{1})\\ &\rho_{2}>\frac{\gamma_{3}\left\|(K_{P}\quad K_{D})\right\|}{1-\gamma_{3}}\\ \text{正数}\quad&\gamma_1>\|\widetilde{\boldsymbol{\Gamma}}(\boldsymbol{\Phi},\dot{\boldsymbol{\Phi}})\| = \|\tilde{C}(\boldsymbol{\Phi},\dot{\boldsymbol{\Phi}})\dot{\boldsymbol{\Phi}}+\widetilde{\boldsymbol{L}}\dot{\boldsymbol{\Phi}}+\widetilde{\boldsymbol{G}}(\boldsymbol{\Phi})\|\\ \text{正数}\quad &\gamma_2>\|\ddot{\boldsymbol{\Phi}}_d\|\\ \text{非负数}\quad1>&\gamma_3\ge\|\boldsymbol I-\boldsymbol M^{-1}(\boldsymbol{\Phi})\hat{M}(\boldsymbol{\Phi})\| \end{align*} \]

矩阵范数采用矩阵最大的奇异值
\(K_P\),\(K_D\) 采用逆运动学控制设计，保证大范围渐进稳定
正数 \(\overline{m}\) 大于 \(M^{-1}(\boldsymbol{\Phi})\) 的最大奇异值和正数 \(\underline{m}\) 小于 \(M^{-1}(\boldsymbol{\Phi})\) 的最小奇异值，再取 \(\hat{M}(\boldsymbol{\Phi})=\frac2{\underline{m}+\overline{m}}\boldsymbol{I}\)，可以保证 \(\left\|\boldsymbol{I}-\boldsymbol{M}^{-1}(\boldsymbol{\Phi})\hat{\boldsymbol{M}}(\boldsymbol{\Phi})\right\|\leqslant\frac{\overline{m}-\underline{m}}{\underline{m}+\overline{m}}=\gamma_{3}<1\)

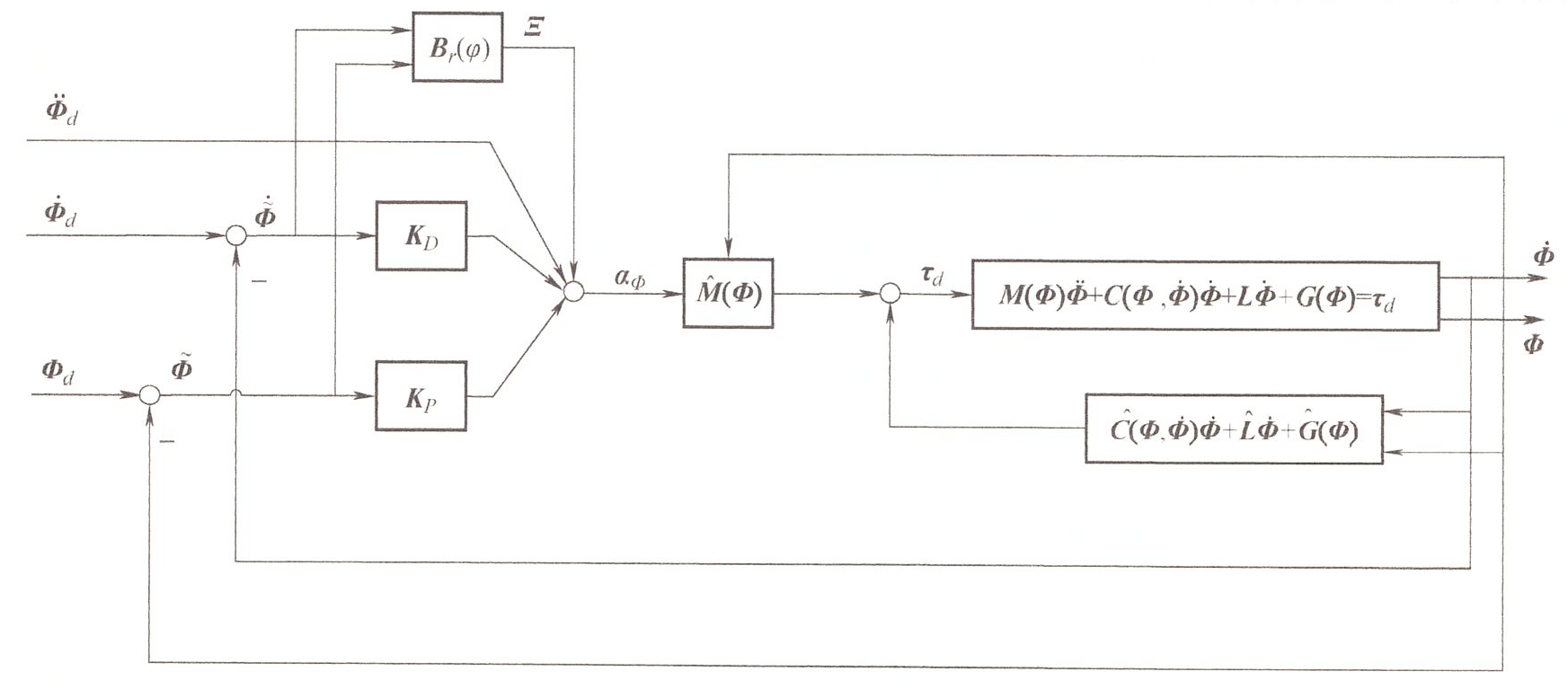
又根据 Lyapunov 稳定性定理，可以证明，保证在不确定性 \(\Delta\) 下 \(\boldsymbol{\Phi}\) 对 \(\boldsymbol{\Phi}_d\) 的渐近跟踪。

自适应控制｜动态估计参数 ¶

在鲁棒控制中，参数的估计是不变的。

自适应控制的思想就是使用在控制过程中观测到的数据，动态更新估计不确定性参数的值。

参数的线性化 ¶

方法：

能测得的变量，如 \(\theta_i\),\(\dot{\theta}_i\),\(\ddot{\theta}_i\) 放在一个矩阵当中
其他系统的参数，当作估计的参数，动态更新

更新 ¶

\[ \Psi = (\Psi_1 \quad \Psi_2 \quad \Psi_3 \quad \Psi_4 \quad \Psi_5 \quad \Psi_6 \quad \Psi_7)^{\mathrm{T}} \]

采用参数线性化形式后，可以基于对 \(\Psi\) 的估计改进逆动力学控制。

\[ \tau_d = Y(\Phi, \dot{\Phi}, \alpha_{\Phi}) \hat{\Psi} = \hat{M}(\Phi) \alpha_{\Phi} + \hat{C}(\Phi, \dot{\Phi}) \dot{\Phi} + \hat{L} \dot{\Phi} + \hat{G}(\Phi) \]

式中，\(\hat{\Psi}\) 是关于 \(\Psi\) 的估计；\(\alpha_{\Phi}\) 仍按式 (8-93) 计算。令

\[ \widetilde{\Psi} = \Psi - \hat{\Psi} \]

\[ \begin{align*} \dot{\varphi} &= \overline{A} \varphi + \overline{B} \hat{M}^{-1}(\Phi) Y(\Phi, \dot{\Phi}, \ddot{\Phi}) \widetilde{\Psi}\\ &= \overline{A} \varphi + \overline{D} \widetilde{\Psi} \end{align*} \]

式中，\(\overline{D} = \overline{B} \hat{M}^{-1}(\Phi) Y(\Phi, \dot{\Phi}, \ddot{\Phi})\)，\(\overline{A}\) 和 \(\overline{B}\) 仍如式 (8-109)，且对于取定的正定 \(Q_L\)，可求得唯一的正定 \(P_L\)，满足李亚普诺夫方程式 (8-110)。自适应控制的核心在于 \(\hat{\Psi}\) 时变，即采用估计更新律

\[ \dot{\hat{\Psi}} = \Gamma^{-1} \overline{D}^{\mathrm{T}} P_L \varphi \]

07 | 运动控制 ¶

前置知识 ¶

旋转编码器——测关节转角转速 ¶

力传感器 ¶

力矩传感器 ¶

单关节：关节空间，输入是速度 ¶

前馈控制 feedforward control ¶

一阶误差 & P 控制 ¶