06 | 动力学 ¶

约 4645 个字预计阅读时间 18 分钟

有哪些力，有哪些运动（2x2 = 4 种组合）

关节空间的运动
末端执行器空间的运动
关节力 / 力矩
末端执行器力 / 力矩

有了运动学，为什么还需要动力学？

运动学可以让我们很好地完成如 Pick and Place 这一类任务，但是对于画一个圆这类的轨迹跟踪任务，运动学就无能为力了。（每时每刻需求解逆运动学不现实）；另外，如果涉及到施加力的控制（使用锉刀），单纯运动学也无法实现。

动力学的引入允许我们更快、更精确地跟随需要的轨迹

没有动力学加入控制回路的机器人能做的事情非常有限，它们速度无法做到很快、负载不能做很重、如果功率很大会非常危险。

干货 | 运动学好像够用了，我们为什么还需要动力学 - 知乎

动力学的目标：如果我们需要控制机器人按照一定的轨迹运动（别忘了轨迹是位置对时间的函数），那么每个关节的驱动器施加多少扭矩（旋转关节）或力（平移关节）

而这一章主要讲解牛顿 - 欧拉迭代动力学方程和拉格朗日动力学方程。

其中，牛顿欧拉方法需要掌握一些刚体力学的知识，拉格朗日方法需要掌握一些分析力学的知识。

前置知识 —— 刚体力学基础 ¶

干货 | 机械臂的动力学（一）：牛顿欧拉法 - 知乎

	linear	angular
惯性	质量 $m$	张量 $\mathbf{I}$
动量	$m\mathbf{v}$	$\mathbf{I}\boldsymbol{\omega}$
外力	力 $\mathbf{F}$	力矩 $\boldsymbol{\tau}$
加速度	线性加速度 $\mathbf{a}$	角加速度 $\boldsymbol{\alpha}$
欧拉方程	$\mathbf{F}=m\mathbf{a}$	$\boldsymbol{\tau}=\mathbf{I}\boldsymbol{\alpha}+\boldsymbol{\omega}\times\mathbf{I}\boldsymbol{\omega}$

叉乘运算 ¶

两个向量 $\vec{a}$ 和 $\vec{b}$ 的叉乘结果是一个新向量 $\vec{c}$:

\[ \vec{c} = \vec{a} \times \vec{b}= |a||b|\sin\theta \]

方向遵循右手定则，垂直于这两个向量所在的平面。

计算方法 ¶

法一：神奇记忆法：

把 $\vec{a}$ 和 $\vec{b}$ 写成下面的矩阵形式

\[ \begin{pmatrix} a_x & a_y & a_z & a_x & a_y & a_z\\ b_x & b_y & b_z & b_x & b_y & b_z \end{pmatrix} \]

去掉第一列和最后一列，剩下的 3 个 2x2 的矩阵（每次滑动 1 格子），计算行列式即可

法 2: 写成 $\mathbf{a} \wedge \mathbf{b}$ 的形式

\[ \mathbf{a} \times \mathbf{b} =\begin{bmatrix}0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \mathbf{b} \]

证明：

\[ \begin{align*} \mathbf{a} \times \mathbf{b} &= \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \times \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} \\ &= \begin{pmatrix} y_1z_2-z_1y_2 \\ z_1x_2-x_1z_2 \\ x_1y_2-y_1x_2 \end{pmatrix} \\ &= \begin{pmatrix} 0 & -z_1 & y_1 \\ z_1 & 0 & -x_1 \\ -y_1 & x_1 & 0 \end{pmatrix} \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} \\ &= \mathbf{a} \wedge \mathbf{b} \end{align*} \]

性质 ¶

基本法则：
- 反交换律：$\mathbf{a} \times \mathbf{b} = -\mathbf{b} \times \mathbf{a}$
- 分配律：$\mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c}$
- 标量兼容性：$\lambda (\mathbf{a} \times \mathbf{b}) = (\lambda \mathbf{a}) \times \mathbf{b} = \mathbf{a} \times (\lambda \mathbf{b})$
几何意义：
- 模长：$|\mathbf{a} \times \mathbf{b}| = |\mathbf{a}||\mathbf{b}|\sin\theta$,$\theta$ 为两向量夹角，对应以 $\mathbf{a}, \mathbf{b}$ 为邻边的平行四边形面积。
- 方向：垂直于 $\mathbf{a}$ 和 $\mathbf{b}$ 所在平面，遵循右手定则（四指从 $\mathbf{a}$ 转向 $\mathbf{b}$，拇指方向为结果方向）。
混合运算：
- 混合积：$(\mathbf{a} \times \mathbf{b}) \cdot \mathbf{c}$ 表示平行六面体体积，满足轮换对称性：$(\mathbf{a} \times \mathbf{b}) \cdot \mathbf{c} = (\mathbf{b} \times \mathbf{c}) \cdot \mathbf{a} = (\mathbf{c} \times \mathbf{a}) \cdot \mathbf{b}$
- 拉格朗日公式：$\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) = \mathbf{b}(\mathbf{a} \cdot \mathbf{c}) - \mathbf{c}(\mathbf{a} \cdot \mathbf{b})$

欧拉第一定律 —— 惯性系 ¶

欧拉第二定律 —— 角动量 ¶

力矩：$\tau = r \times F$

特别注意叉乘的顺序

惯性张量 ¶

参考资料：转动惯量、惯性张量、转动动能的推导 - 知乎机器人动力学建模之理解惯性张量-CSDN博客

\[ ^c\mathbf{I} = \begin{pmatrix} \sum m_i(y_i^2 + z_i^2) & -\sum m_i x_i y_i & -\sum m_i x_i z_i \\ -\sum m_i x_i y_i & \sum m_i(x_i^2 + z_i^2) & -\sum m_i y_i z_i \\ -\sum m_i x_i z_i & -\sum m_i y_i z_i & \sum m_i(x_i^2 + y_i^2) \end{pmatrix}= \begin{pmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xz} & -I_{yz} & I_{zz} \end{pmatrix} \]

\[ \begin{align*} I_{xx} &= \int_B (y^2 + z^2) \rho(x, y, z) \mathrm{d}V \\ I_{yy} &= \int_B (x^2 + z^2) \rho(x, y, z) \mathrm{d}V \\ I_{zz} &= \int_B (x^2 + y^2) \rho(x, y, z) \mathrm{d}V \\ I_{xy} &= \int_B xy \rho(x, y, z) \mathrm{d}V \\ I_{xz} &= \int_B xz \rho(x, y, z) \mathrm{d}V \\ I_{yz} &= \int_B yz \rho(x, y, z) \mathrm{d}V \end{align*} \]

转动惯量是绕着某个轴的，而惯性张量是绕着某个点的。
转动惯量是标量，惯性张量是矩阵。

三个对角元素 $I_{xx}, I_{yy}, I_{zz}$( 称为惯性矩 )；$I_{xx}$ 对应绕 x 轴转动惯量，$I_{yy}$ 对应绕 y 轴转动惯量，$I_{zz}$ 对应绕 z 轴转动惯量。
非对角元素称为惯性积

常见的转动惯量

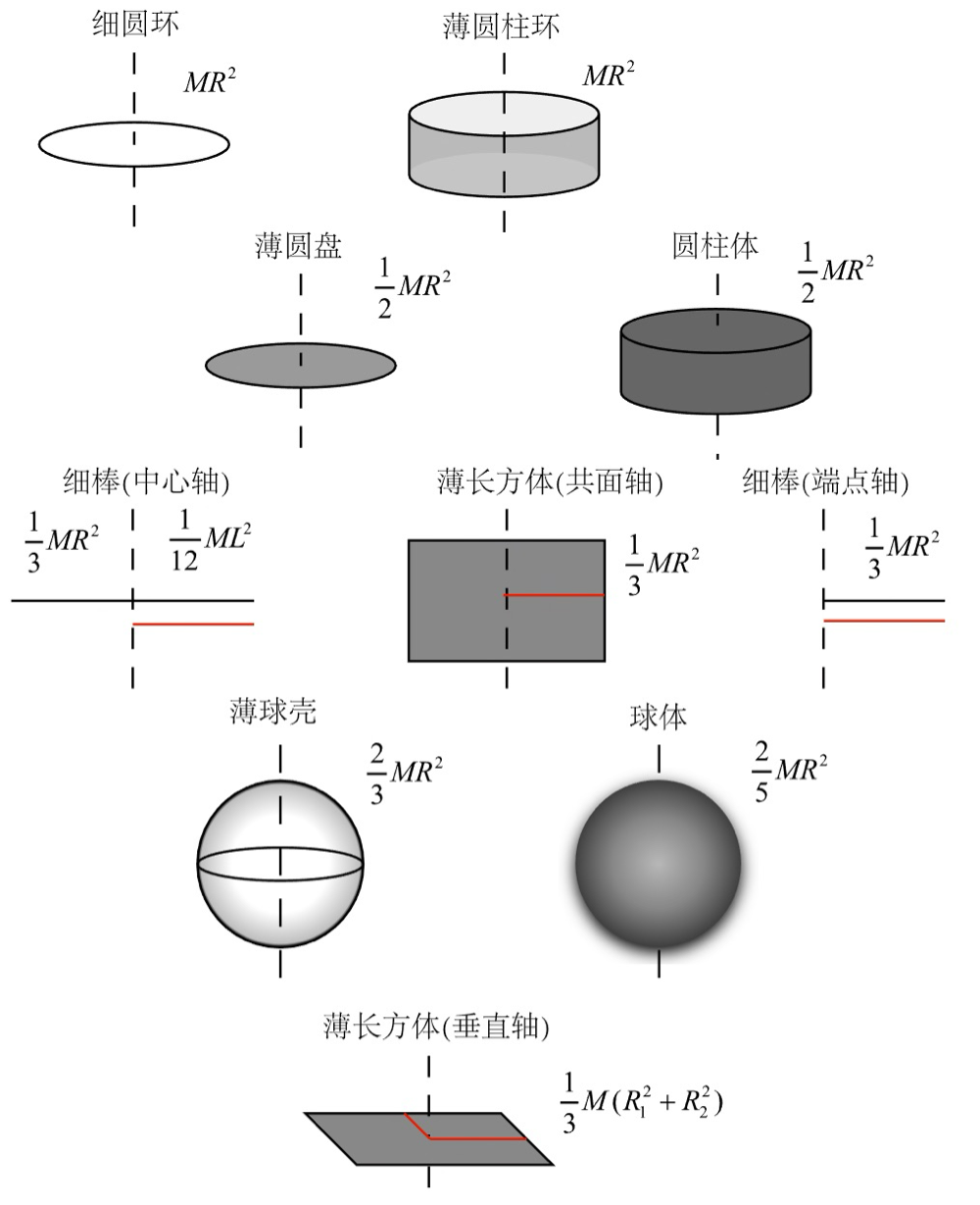
积分 trick ¶

请务必回顾一下微积分下当中多元积分相关的内容，不然这部分会影响理解

多元积分

画出积分区域
确定上下左右限
写出累次积分
逐个计算定积分

极坐标换元

\[ \begin{aligned} &x=x(u,v),y=y(u,v),\quad J=\frac{\partial(x,v)}{\partial(u,v)}=\begin{vmatrix}\frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}\end{vmatrix}\neq0\\&\iint f(x,y)\mathrm{~d}x\mathrm{d}y=\iint_{D}f[x(u,v),y(u,v)]\quad|J|\mathrm{~d}u\mathrm{d}v\\ &令x=\rho\cos\theta,y=\rho\sin\theta\quad J=\begin{vmatrix}\cos\theta&-\rho\sin\theta\\\sin\theta&\rho\cos\theta\end{vmatrix}=\rho\\ &\therefore\mathrm{d}x\mathrm{d}y=\rho\mathrm{d}\rho\mathrm{d}\theta \end{aligned} \]

对称性

对称性：（$y=x$ 对称）
奇偶性：x 轴，y 轴等；利用被积函数奇偶性

方法：拆分函数；拆分积分域；画辅助线

平移 ¶

平行移轴定理

\[ ^AI=^CI+m(P_c^TP_cI_3-P_cP_c^T) \]

证明

惯性张量平移和旋转复合变换的一般形式及其应用

旋转 ¶

假设物体的质心在坐标系 $0$ 中为 $O_0$，在坐标系 $b$ 中为 $O_b$

物体的转动惯量在坐标系 $i$ 中为 $I^b$，物体的转动惯量在坐标系 $0$ 中为 $I^0$。

\[ ^bI=(_b^0R^T)(^0I)(_b^0R) \]

\[ {}^0I=({}_b^0R)({}^bI)({}_b^0R^T)\]

证明

动能这个标量在不同坐标系下是一致的，可以有下面的式子

$$ T = frac{1}{2}(^{0}omegaT)(^{0}I)(omega) $$

$$ T = frac{1}{2}(^{b}omegaT)(^{b}I)(omega) $$

展开第一个式子，有

$$ begin{align} T &= frac{1}{2}(^{0}omegaT)(^{0}I)(omega)\ &= frac{1}{2}(^{b}Romega)^T(I)(^{0}Romega)\ &= frac{1}{2}(^{b}omegaT)(^{b}RT)(^{0}I)(omega) end{align}R)(^{b} $$

所以

$$ {}^{b}I = ({}^{0}RT)({}^{0}I)({}R) $$

进一步，两边左乘 $({}^{0}R)$，右乘 $({}^{b}R^T)$，可得：

$$ {}^{0}I = ({}^{0}R)({}}I)({^{0}RT) $$

牛顿欧拉法迭代动力学方程 ¶

先进行外推，再进行内推

先进行外推，得到每个连杆的加速度、质心加速度：目的是根据牛顿 - 欧拉方程，计算出每个连杆的力和力矩

$$ begin{align} F_{i}&=m_{i}dot{boldsymbol{v}}{i}\ N}&=I_{Ci}dot{boldsymbol{omega}{i}+boldsymbol{omega} end{align}times I_{Ci}boldsymbol{omega}_{i} $$

再进行内推，得到每个关节的力和力矩。

推导机械臂动力学的牛顿欧拉法是一个递归算法

注意旋转关节 R 和平移关节 P 的公式区别

外推 ¶

平动

物理量	公式
角速度	$^{i+1}\omega_{i+1} = {}^{i+1}_i R \cdot {}^i \omega_i$
角加速度	$^{i+1}\dot{\omega}_{i+1} = {}^{i+1}_i R \cdot {}^i \dot{\omega}_i$
加速度	$^{i+1}\dot{v}_{i+1} = {}^{i+1}_i R \left[ {}^i \dot{\omega}_i \times O_{i+1} + {}^i \omega_i \times \left( {}^i \omega_i \times ^iO_{i+1} \right) + {}^i \dot{v_i} \right] + 2 \cdot {}^{i+1} \omega_{i+1} \times \dot{d}_{i+1} ^{i+1} \hat{Z}_{i+1} \ + \ \ddot{d}_{i+1}\cdot {}^{i+1} \hat{Z}_{i+1}$ 注意这里不是 $2^{i+1}$, 不要看错
质心加速度	$^{i+1}\dot{v}_{C_{i+1}} = {}^{i+1}_i \dot{\omega}_{i+1} \times {}^{i+1} P_{C_{i+1}} + {}^{i+1} \omega_{i+1} \times \left( {}^{i+1} \omega_{i+1} \times {}^{i+1} P_{C_{i+1}} \right) + {}^{i+1} \dot{v}_{i+1}$
力	$^{i+1} F_{i+1} = m_{i+1} \cdot {}^{i+1}_i \dot{v}_{C_{i+1}}$
力矩	$^{i+1}N_{i+1} = {}^{C_{i+1}} I_{i+1} \cdot {}^{i+1}\dot{\omega}_{i+1} + {}^{i+1} \omega_{i+1} \times{}^{C_{i+1}} I_{i+1} \cdot {}^{i+1} \omega_{i+1}$

转动

物理量	公式
角速度	$^{i+1}\omega_{i+1} ={}^{i+1}_i R \cdot {}^i \omega_i + \dot{\theta}_{i+1} \cdot {}^{i+1} \hat{Z}_{i+1}$
角加速度	$^{i+1}\dot{\omega}_{i+1} ={}^{i+1}_i R \cdot {}^i \dot{\omega}_i + {}^{i+1}_i R \cdot {}^i \omega_i \times \dot{\theta}_{i+1} \cdot {}^{i+1} \hat{Z}_{i+1} + \ddot{\theta}_{i+1} \cdot {}^{i+1} \hat{Z}_{i+1}$
加速度	$^{i+1}\dot{v}_{i+1} ={}^{i+1}_i R \left[ {}^i \dot{\omega}_i \times O_{i+1} + {}^i \omega_i \times \left( {}^i \omega_i \times {}^iO_{i+1} \right) + {}^i \dot{v_i} \right]$
质心加速度	$^{i+1}\dot{v}_{C_{i+1}} ={}^{i+1}_i \dot{\omega}_{i+1} \times {}^{i+1} P_{C_{i+1}} + {}^{i+1} \omega_{i+1} \times \left( {}^{i+1} \omega_{i+1} \times {}^{i+1} P_{C_{i+1}} \right) + {}^{i+1} \dot{v}_{i+1}$
力	$^{i+1} F_{i+1} =m_{i+1} \cdot {}^{i+1}_i \dot{v}_{C_{i+1}}$
力矩	$^{i+1}N_{i+1} ={}^{C_{i+1}} I_{i+1} \cdot {}^{i+1}\dot{\omega}_{i+1} + {}^{i+1} \omega_{i+1} \times{}^{C_{i+1}} I_{i+1} \cdot {}^{i+1} \omega_{i+1}$

注意事项

角速度初始值： ${}^0 \omega_0 = (0,0,0)^T$
角加速度初始值： ${}^0 \dot{\omega}_0 = (0,0,0)^T$
加速度初始值（含重力）： ${}^0 v_0 = (0, g, 0)^T$

为什么 ${}^0 v_0 = (0, g, 0)^T$

这里在推导的时候没有考虑重力，是因为相当于考虑连杆坐标系 {0} 以加速度 $G$ 运动，$G$ 与重力大小相当，方向相反

这里需要了解一下惯性力的有关知识，惯性力是一个假想的力，其方向与加速度方向相反，大小为 $m\cdot a$

最简单的应用：高中物理，分离法进行受力分析，给物体施加一个惯性力，然后进行受力分析，有加速度的物体就可以看成是受力平衡的物体进行分析了

$g$ 不在 z 轴的原因：因为书上是 RRR 的机械臂，转轴垂直于纸面，建系的时候重力在 y 轴方向而不是 z 轴方向，所以 $g$ 不在 z 轴上

内推 ¶

连杆力 ${}^i f_i = {}_{i+1}^i R {}^{i+1} f_{i+1} + {}^i F_i$

连杆力矩 ${}^i n_i = {}^i N_i + {}_{i+1}^i R {}^{i+1} n_{i+1} + {}^i P_{C_i} \times {}^i F_i + {}^i O_{i+1} \times {}_{i+1}^i R {}^{i+1} f_{i+1}$

关节力 / 力矩

转动：$\tau_i = {}^i n_i^T \cdot{}^i \hat{Z}_i$
平动：$\tau_i= {}^i f_i^T \cdot {}^i \hat{Z}_i$

注意旋转关节 R 和平移关节 P 的公式区别

推导方法

静力平衡

对于一个连杆，一共有四个力，

所以可以计算出为了平衡，关节需要额外提供的力 / 力矩

$$ F_{i}=f_{i}-f_{i+1}\ N_{i}=n_{i}-n_{i+1}+(-p_{c})times f_{i}+(p_{i+1}-p_{c})times(-f_{i+1}) $$

注意，这里需要转化到一个坐标系下面计算，所以需要用到旋转矩阵

前置知识 —— 分析力学基础 ¶

拉格朗日力学
- 达朗贝尔原理
- 拉格朗日方程；拉格朗日关系
哈密顿力学
- 哈密顿原理

从零学分析力学（拉格朗日力学篇） - 知乎

牛顿力学又称为矢量力学，基于相对性原理和伽利略变换。但是在描述复杂系统（如单摆）的时候，比较复杂。所以使用广义坐标来描述系统的状态。

广义坐标：不是特定坐标，描述力学系统状态即可；

力学系统所受理想约束力所做的虚功为 0

达朗贝尔原理：拉格朗日力学中的第二个基本原理 ¶

\[ \sum_{i=1}^{n} (\vec{F}_i - m_i \ddot{\vec{r}}_i) \cdot \delta \vec{r}_i = 0 \]

没有约束的情况下，$\delta \vec{r}_i$ 相互独立，所以前面系数为 0，即牛顿第二定律

拉格朗日方程：描述物体运动的方程 ¶

地位如同牛顿第二定律

$\delta$ 与 $d$ 运算规则基本相同
消去的一个思路：利用广义坐标相互独立，所以系数为 0
另一个思路：矢量的化简比较复杂，标量化简较为简单

拉格朗日函数：$L = T-U$ 只在保守系下成立，$T$ 为动能，$U$ 为势能

\[ Q_a = \frac{d}{dt} \left( \frac{\partial T}{\partial \dot{q}_a} \right) - \frac{\partial T}{\partial q_a} = 0 \]

T: 动能 ,$q_a$ 广义坐标，$\dot{q}_a$ 广义速度，$Q_a$ 广义力 , 广义动量 $P_{\alpha} = \frac{\partial T}{\partial \dot{q_\alpha}}$

\[ \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}_a} \right) - \frac{\partial L}{\partial q_a} = 0 \]

保守体系下，完整系统的拉格朗日方程

泛函求极值；欧拉方程 ¶

欧拉 - 拉格朗日方程

\[ \frac{d}{dx}\left( \frac{\partial F}{\partial \dot{y}} \right) - \frac{\partial F}{\partial y} = 0 \]

欧拉方程是泛函求极值的一个条件，形式和保守体系下的拉格朗日方程类似。

所以隐含着：物体的运动对应着某个量取极值

哈密顿原理 ¶

系统的运动是使作用量 $S$ 取得极值的运动，也就是说物理系统倾向于选择更省力、更节能的方式来运动

\[ Energy = K + U = \sum_{i=1}^{n} \frac{1}{2} m_i \dot{r}_i^2 + \sum_{i=1}^{n} m_i g h_i \]

Hamiltonian：哈密顿量，系统的总能量

$H = K+U$

\[ H = \frac{P^2}{2ml^2} - mgl \cos(\theta) \]

满足两个一阶微分方程

\[ \dot{q} = \frac{\partial H}{\partial P}, \dot{P} = -\frac{\partial H}{\partial q} \]

把运动化到了 face space 上面；知道了任意一点的位置和动量，就可以知道它的运动轨迹；

Solutions to the Problem Sheet: Lagrangian and Hamiltonian Mechanics in Under 20 Minutes — Physics with Elliot

拉格朗日动力学方程 ¶

计算思路 1: 直接计算动能势能 ¶

动能

列写质心的坐标，对关节求偏导得到 $J_v$
使用列写世界坐标系下各 z 轴的方法得到 $J_\omega$

\[ k_{i}=\frac{1}{2}m_{i}\boldsymbol{v}_{C_{i}}^{\mathrm{T}}\boldsymbol{v}_{C_{i}}+\frac{1}{2}\boldsymbol{\omega}_{i}^{T0}\boldsymbol{R}^{C_{i}}\boldsymbol{I}_{i}^{0}\boldsymbol{R}^{\mathrm{T}}\boldsymbol{\omega}_{i} \]

势能

就直接列写连杆的质心和关节的重力势能即可

计算思路 2: 矩阵 ¶

首先计算雅可比矩阵、旋转矩阵、惯性张量，这一步非常重要且基础，后续的计算都依赖于这一步 ,~~算错的话可能一两个小时白干~~
计算 $\boldsymbol{M}(\boldsymbol{\Phi})$, $\boldsymbol{C}(\boldsymbol{\Phi},\dot{\boldsymbol{\Phi}})$ 和 $\boldsymbol{G}(\boldsymbol{\Phi})$
带入公式，求解动力学方程

\[ \boldsymbol{M}(\boldsymbol{\Phi})\ddot{\boldsymbol{\Phi}}+\boldsymbol{C}(\boldsymbol{\Phi},\dot{\boldsymbol{\Phi}})\dot{\boldsymbol{\Phi}}+\boldsymbol{B}\dot{\boldsymbol{\Phi}}+\boldsymbol{G}(\boldsymbol{\Phi})=\boldsymbol{\tau} \]

每一项的计算方法如下：

$\boldsymbol{M}(\boldsymbol{\Phi})=\sum_{i=1}^{N}(m_{i}(\boldsymbol{J}_{P}^{(i)})^{\mathrm{T}}\boldsymbol{J}_{P}^{(i)}+(\boldsymbol{J}_{0}^{(i)})^{\mathrm{T}0}\boldsymbol{R}^{C_{i}}\boldsymbol{I}_{ii}^{0}\boldsymbol{R}^{\mathrm{T}}\boldsymbol{J}_{0}^{(i)})$，M 一般可以化简，如果形式太过复杂，观察一下有没有正负号写错了
$\boldsymbol{C}(\boldsymbol{\Phi},\dot{\boldsymbol{\Phi}})= \left.\left(\begin{array}{ccccccc}\sum_{k}c_{k11}\dot{\phi}_{k}&\sum_{k}c_{k21}\dot{\phi}_{k}&\cdots&\sum_{k}c_{kj1}\dot{\phi}_{k}&\cdots&\sum_{k}c_{kN1}\dot{\phi}_{k}\\\sum_{k}c_{k12}\dot{\phi}_{k}&\sum_{k}c_{k22}\dot{\phi}_{k}&\cdots&\sum_{k}c_{kj2}\dot{\phi}_{k}&\cdots&\sum_{k}c_{kN2}\dot{\phi}_{k}\\\vdots&\vdots&&\vdots&&\vdots\\\sum_{k}c_{k11}\dot{\phi}_{k}&\sum_{k}c_{k21}\dot{\phi}_{k}&\cdots&\sum_{k}c_{kj1}\dot{\phi}_{k}&\cdots&\sum_{k}c_{kNi}\dot{\phi}_{k}\\\vdots&\vdots&&\vdots&&\vdots\\\sum_{k}c_{k1N}\dot{\phi}_{k}&\sum_{k}c_{k2N}\dot{\phi}_{k}&\cdots&\sum_{k}c_{kjN}\dot{\phi}_{k}&\cdots&\sum_{k}c_{kNN}\dot{\phi}_{k}\end{array}\right.\right)$
$c_{jki}=\frac{1}{2}\left(\frac{\partial m_{ik}}{\partial\phi_{j}}+\frac{\partial m_{ij}}{\partial\phi_{k}}-\frac{\partial m_{kj}}{\partial\phi_{i}}\right)=c_{kji}$
$G(\boldsymbol{\Phi})=\binom{g_1(\boldsymbol{\Phi})}{g_N(\boldsymbol{\Phi})}$, 其中 $g_i(\boldsymbol{\Phi})=\frac{\partial u}{\partial\phi_i}=-\sum_{j=1}^Nm_j^0g^\mathrm{T} \frac{\partial^0\boldsymbol{P}_{C_j}}{\partial\phi_i}$
$B=\mathrm{diag}(\begin{array}{ccc}b_1&\cdots&b_N\end{array})$,$b_i$ 为折算到关节 $i$ 的粘性摩擦参数 (Viscous Friction Coefficient)

物理含义 ¶

动力学方程的物理含义

这两篇当中有比较详细的关于三个矩阵的每个元素的具体含义

干货 | 机械臂的动力学（三）：理解动力学方程上篇 - 知乎

干货 | 机械臂的动力学 ( 四）：理解动力学方程下篇 - 知乎

质量矩阵：
- 对角元素：它正是由每个关节自身加速运动（驱动所有在其之后的连杆加速运动）所需要的扭矩
- 非对角：其他关节加速运动（造成其之后的连杆加速运动）对这个关节的影响叠加而成 . 反映的正是第二个关节运动时第一个关节需要承担的惯性力

例子

题目 1 RP 机械臂

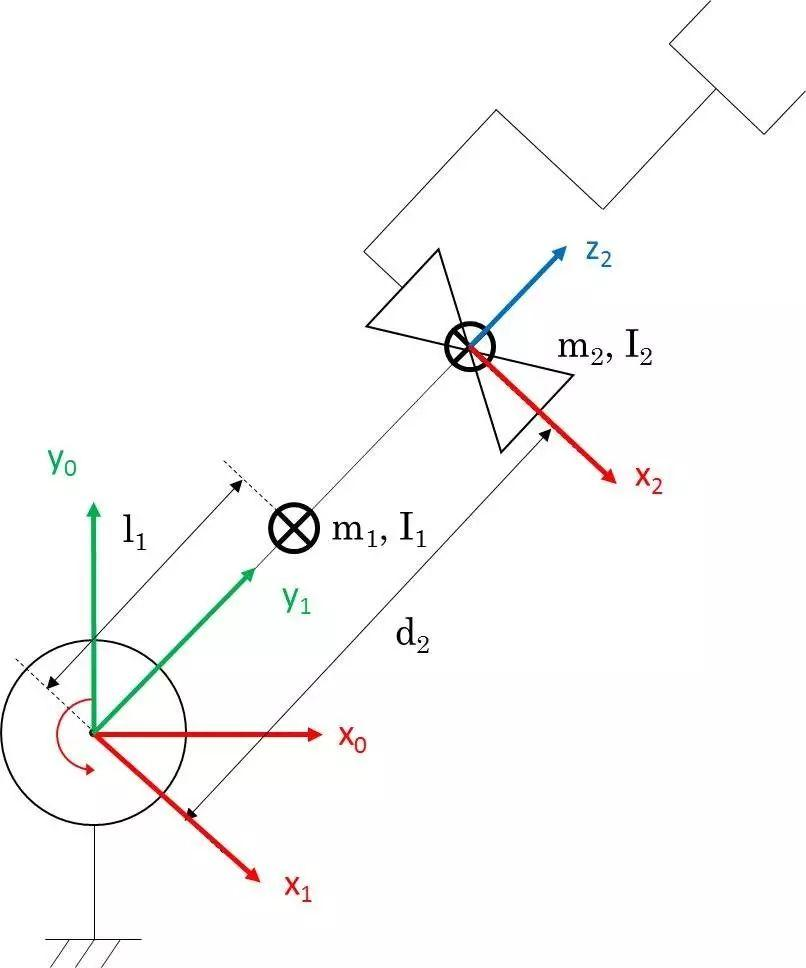
$$ ^0J_{v1} = begin{bmatrix} -l_1 sin theta_1 & 0 \ l_1 cos theta_1 & 0 \ 0 & 0 end{bmatrix}; ^0J_{v2} = begin{bmatrix} -d_2 sin theta_1 & cos theta_1 \ d_2 cos theta_1 & sin theta_1 \ 0 & 0 end{bmatrix} $$

$$ ^{c_1}J_{omega1} = begin{bmatrix} 0 & 0 \ 0 & 0 \ 1 & 0 end{bmatrix}; ^{c_2}J_{omega2} = begin{bmatrix} 0 & 0 \ 0 & 0 \ 1 & 0 end{bmatrix} $$

注意这里我们求的不是 end effector 的雅可比矩阵，而是每一根连杆的质心的运动相对于关节运动的雅可比矩阵（在求解时可以把质心当作 end effector 来理解）。最后，我们可以得到这个RP机械臂的质量矩阵：

$$ M = begin{bmatrix} m_1 l_1^2 + I_{zz1} + m_2 d_2^2 + I_{zz2} & 0 \ 0 & m_2 end{bmatrix} $$

题目 2 PRR 机械臂

$$ M=begin{bmatrix}m_1+m_2+m_3&times&times\times&l_{zz2}+m_2l_2^{2+l_{zz3}+m_3({a_2}}2+{l_3}^2+2a_2l_3cos q_3)&times\times&times&l_{zz3}+m_3l_3^2end{bmatrix} $$

$$ M=begin{bmatrix}times&m_2l_2c_2+m_3(l_3c_2c_3+a_2c_2-l_3s_2s_3)&-m_3(l_3s_2s_3-l_3c_2c_3)\times&times&l_{zz3}+m_3(l_3^2+a_2l_3c_3)\times&times&timesend{bmatrix} $$

科里奥利力与离心力矩阵：

\[ V(\boldsymbol{q},\dot{\boldsymbol{q}})=C(\boldsymbol{q},\dot{\boldsymbol{q}})\begin{bmatrix}\dot{q}_1^2\\\vdots\\\dot{q}_n^2\end{bmatrix}+\boldsymbol{B}(\boldsymbol{q},\dot{\boldsymbol{q}})\begin{bmatrix}\dot{q}_1\dot{q}_2\\\dot{q}_1\dot{q}_3\\\vdots\\\dot{q}_{n-2}\dot{q}_n\\\dot{q}_{n-1}\dot{q}_n\end{bmatrix} \]

性质 ¶

$\dot{\boldsymbol{M}}(\boldsymbol{\Phi})-2\boldsymbol{C}(\boldsymbol{\Phi},\dot{\boldsymbol{\Phi}})$ 是反对称的
惯性矩阵 $\boldsymbol{M}(\boldsymbol{\Phi})$ 是正定的，因为机器人的总动能是非负的，所以惯性矩阵是正定的

题目 ¶

动力学方程求解 ¶

个人倾向于拉格朗日方法直接列写动能势能

其他方法需要注意带对公式、耐心计算

惯性张量相关 ¶

学会积分

均质圆柱 , 原点位于质心 $Z$ 重合于转轴 , 求 $I_{xy},I_{zz}$

	linear	angular
惯性	质量 \(m\)	张量 \(\mathbf{I}\)
动量	\(m\mathbf{v}\)	\(\mathbf{I}\boldsymbol{\omega}\)
外力	力 \(\mathbf{F}\)	力矩 \(\boldsymbol{\tau}\)
加速度	线性加速度 \(\mathbf{a}\)	角加速度 \(\boldsymbol{\alpha}\)
欧拉方程	\(\mathbf{F}=m\mathbf{a}\)	\(\boldsymbol{\tau}=\mathbf{I}\boldsymbol{\alpha}+\boldsymbol{\omega}\times\mathbf{I}\boldsymbol{\omega}\)

物理量	公式
角速度	\(^{i+1}\omega_{i+1} = {}^{i+1}_i R \cdot {}^i \omega_i\)
角加速度	\(^{i+1}\dot{\omega}_{i+1} = {}^{i+1}_i R \cdot {}^i \dot{\omega}_i\)
加速度	\(^{i+1}\dot{v}_{i+1} = {}^{i+1}_i R \left[ {}^i \dot{\omega}_i \times O_{i+1} + {}^i \omega_i \times \left( {}^i \omega_i \times ^iO_{i+1} \right) + {}^i \dot{v_i} \right] + 2 \cdot {}^{i+1} \omega_{i+1} \times \dot{d}_{i+1} ^{i+1} \hat{Z}_{i+1} \ + \ \ddot{d}_{i+1}\cdot {}^{i+1} \hat{Z}_{i+1}\) 注意这里不是 \(2^{i+1}\), 不要看错
质心加速度	\(^{i+1}\dot{v}_{C_{i+1}} = {}^{i+1}_i \dot{\omega}_{i+1} \times {}^{i+1} P_{C_{i+1}} + {}^{i+1} \omega_{i+1} \times \left( {}^{i+1} \omega_{i+1} \times {}^{i+1} P_{C_{i+1}} \right) + {}^{i+1} \dot{v}_{i+1}\)
力	\(^{i+1} F_{i+1} = m_{i+1} \cdot {}^{i+1}_i \dot{v}_{C_{i+1}}\)
力矩	\(^{i+1}N_{i+1} = {}^{C_{i+1}} I_{i+1} \cdot {}^{i+1}\dot{\omega}_{i+1} + {}^{i+1} \omega_{i+1} \times{}^{C_{i+1}} I_{i+1} \cdot {}^{i+1} \omega_{i+1}\)

物理量	公式
角速度	\(^{i+1}\omega_{i+1} ={}^{i+1}_i R \cdot {}^i \omega_i + \dot{\theta}_{i+1} \cdot {}^{i+1} \hat{Z}_{i+1}\)
角加速度	\(^{i+1}\dot{\omega}_{i+1} ={}^{i+1}_i R \cdot {}^i \dot{\omega}_i + {}^{i+1}_i R \cdot {}^i \omega_i \times \dot{\theta}_{i+1} \cdot {}^{i+1} \hat{Z}_{i+1} + \ddot{\theta}_{i+1} \cdot {}^{i+1} \hat{Z}_{i+1}\)
加速度	\(^{i+1}\dot{v}_{i+1} ={}^{i+1}_i R \left[ {}^i \dot{\omega}_i \times O_{i+1} + {}^i \omega_i \times \left( {}^i \omega_i \times {}^iO_{i+1} \right) + {}^i \dot{v_i} \right]\)
质心加速度	\(^{i+1}\dot{v}_{C_{i+1}} ={}^{i+1}_i \dot{\omega}_{i+1} \times {}^{i+1} P_{C_{i+1}} + {}^{i+1} \omega_{i+1} \times \left( {}^{i+1} \omega_{i+1} \times {}^{i+1} P_{C_{i+1}} \right) + {}^{i+1} \dot{v}_{i+1}\)
力	\(^{i+1} F_{i+1} =m_{i+1} \cdot {}^{i+1}_i \dot{v}_{C_{i+1}}\)
力矩	\(^{i+1}N_{i+1} ={}^{C_{i+1}} I_{i+1} \cdot {}^{i+1}\dot{\omega}_{i+1} + {}^{i+1} \omega_{i+1} \times{}^{C_{i+1}} I_{i+1} \cdot {}^{i+1} \omega_{i+1}\)