05 | 轨迹规划 ¶
约 3667 个字 291 行代码 预计阅读时间 18 分钟
为每个关节计算连续的运动轨迹,使末端执行器在空间中从点 A 移动到点 B
难点:
- 求解方程 ; 公式理解
- 列写方程之后,检查未知数个数和方程个数是否匹配
| 特性 | 关节空间规划 | 笛卡尔空间规划 |
|---|---|---|
| 定义 | 在关节空间中规划每个关节的运动轨迹,使末端执行器达到目标位置。 | 在笛卡尔空间中直接规划末端执行器的运动轨迹。 |
| 优点 | 计算简单,适合大多数机器人控制器。 | 轨迹直观,便于控制末端执行器的运动路径。 |
| 缺点 | 末端执行器的路径可能不直观,可能出现不必要的绕行。 | 计算复杂,可能需要逆运动学求解,增加计算负担。 |
| 适用场景 | 对路径形状要求不高的任务,例如点到点的运动。 | 对路径形状有严格要求的任务,例如绘图或焊接。 |
| 插值方法 | 直接对关节角度进行插值。 | 需要对末端位置或姿态进行插值,可能涉及旋转矩阵或四元数的处理。 |
| 运动平滑性 | 关节运动平滑,但末端执行器路径可能不平滑。 | 末端执行器路径平滑,但可能导致关节运动不平滑。 |
关节空间规划 ¶
任务描述:给定末端工具坐标系的位置和姿态,逆运动学求解出各个位姿对应的关节角,然后利用插值计算每个关节的运动轨迹。
| 方法 | 平滑性 | 计算复杂度 | 加速度连续性 | 适用场景 |
|---|---|---|---|---|
| 线性插值 | 低(速度突变) | 低 | 不连续 | 简单、低速 |
| 抛物线过渡 | 中(速度连续) | 中 | 不连续 | 中等速度,允许加速度突变 |
| 分段三次多项式 | 高(速度 / 加速度连续) | 中高 | 连续 | 平滑加减速的中高速运动 |
| 五次多项式 | 极高(全局连续) | 高 | 连续 | 高精度、高动态性能需求 |
线性插值 ¶
线性插值是一种简单的轨迹规划方法,通过在起点和终点之间进行线性插值来计算中间点的位置。其公式如下:
其中:
- \(\phi_0\) 为起始位置,
- \(\phi_f\) 为终止位置,
- \(t\) 为当前时间,
- \(T\) 为总时间。
线性插值的优点是计算简单,适用于对路径平滑性要求不高的场景,但其缺点是速度和加速度可能会出现突变。
import numpy as np
def linear_interpolation(start, end, t, duration):
"""
线性插值轨迹规划
:param start: 起始点坐标
:param end: 终点坐标
:param t: 当前时间
:param duration: 总时长
:return: 当前时刻的位置
"""
if t < duration:
x_array = start * (1 - t / duration) + end * (t / duration)
x_angles = inverse_kinematics(x_array)
else:
x_angles = inverse_kinematics(end)
return x_angles
三次多项式:规划位置 & 速度 ¶
这里有四个未知数,所以需要四个约束条件,选择初始位置、初始速度、终止位置、终止速度(一般都是给定的)
用给定的数据求解方程,得到四个系数,然后就可以得到轨迹方程。
多项式规划的思想可以用在指定导数的题目上面,不一定是轨迹的规划
三次 + 中间点 ¶
指定中间点速度
每一段都使用三次多项式进行规划。
- 前后两段斜率符号相同:速度取平均值
- 前后两段斜率符号不同:速度取 0
不指定中间点速度
有八个未知数,所以需要八个约束条件,一种方式是
- 位置约束:第一段起点终点,第二段起点终点
- 速度约束:第一段起点速度,第二段终点速度,中间点速度相等
- 加速度联系约束:中间点加速度相等
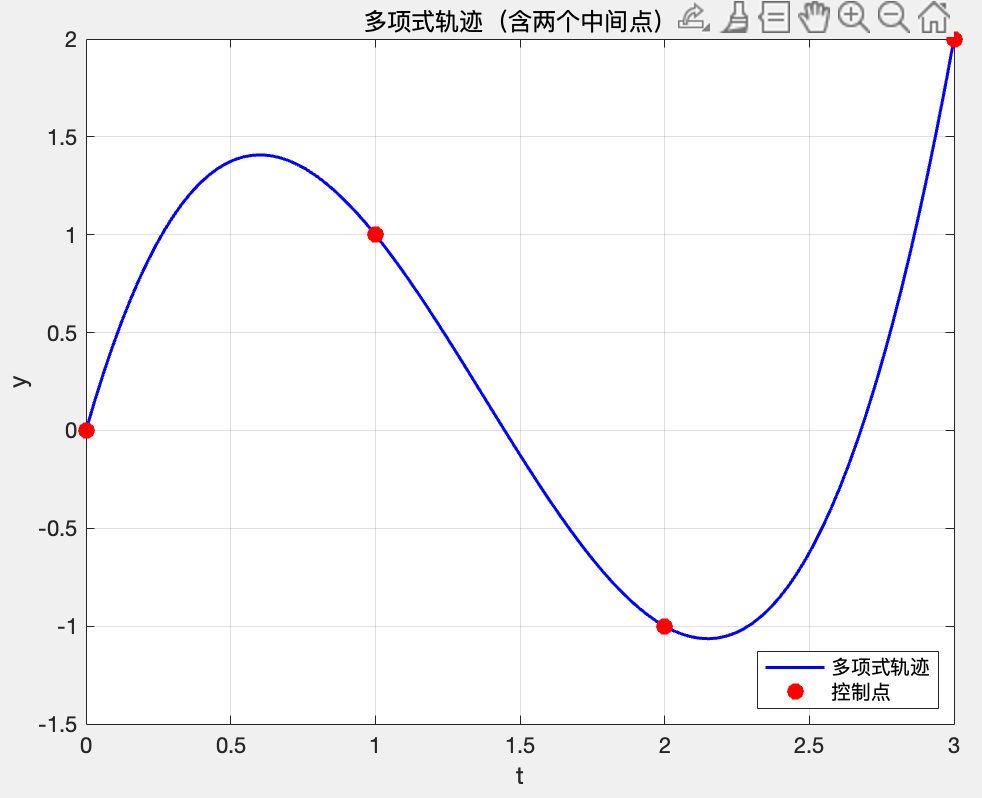
| 三次 + 两个中间点 | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | |
\(\begin{cases} a_{10} = \phi_0 \\ a_{11} = 0 \\ a_{12} = -\frac{3(\phi_0t_{\textrm{f2}}^2 + \phi_gt_{\textrm{f1}}^2 - \phi_vt_{\textrm{f1}}^2 - \phi_vt_{\textrm{f2}}^2 + 2\phi_0t_{\textrm{f1}}t_{\textrm{f2}} - 2\phi_vt_{\textrm{f1}}t_{\textrm{f2}})}{2t_{\textrm{f1}}^2t_{\textrm{f2}}(t_{\textrm{f1}} + t_{\textrm{f2}})} \\ a_{13} = \frac{\phi_0t_{\textrm{f2}}^2 + 3\phi_gt_{\textrm{f1}}^2 - 3\phi_vt_{\textrm{f1}}^2 - \phi_vt_{\textrm{f2}}^2 + 4\phi_0t_{\textrm{f1}}t_{\textrm{f2}} - 4\phi_vt_{\textrm{f1}}t_{\textrm{f2}}}{2t_{\textrm{f1}}^3t_{\textrm{f2}}(t_{\textrm{f1}} + t_{\textrm{f2}})} \\ a_{20} = \phi_v \\ a_{21} = -\frac{3(\phi_0t_{\textrm{f2}}^2 - \phi_gt_{\textrm{f1}}^2 + \phi_vt_{\textrm{f1}}^2 - \phi_vt_{\textrm{f2}}^2)}{2t_{\textrm{f1}}t_{\textrm{f2}}(t_{\textrm{f1}} + t_{\textrm{f2}})} \\ a_{22} = \frac{3(\phi_0t_{\textrm{f2}} + \phi_gt_{\textrm{f1}} - \phi_vt_{\textrm{f1}} - \phi_vt_{\textrm{f2}})}{t_{\textrm{f1}}t_{\textrm{f2}}(t_{\textrm{f1}} + t_{\textrm{f2}})} \\ a_{23} = -\frac{3\phi_0t_{\textrm{f2}}^2 + \phi_gt_{\textrm{f1}}^2 - \phi_vt_{\textrm{f1}}^2 - 3\phi_vt_{\textrm{f2}}^2 + 4\phi_gt_{\textrm{f1}}t_{\textrm{f2}} - 4\phi_vt_{\textrm{f1}}t_{\textrm{f2}}}{2t_{\textrm{f1}}t_{\textrm{f2}}^3(t_{\textrm{f1}} + t_{\textrm{f2}})} \end{cases}\)
五次多项式:规划位置 & 速度 & 加速度 ¶
思路比较类似。
六个未知数 , 就可以指定起点终点的位置、速度、加速度,然后求解方程。
def quintic_polynomial(start, end, t, duration):
"""
五次多项式轨迹规划
:param start: 起始点坐标
:param end: 终点坐标
:param t: 当前时间
:param duration: 总时长
:return: 当前时刻的位置
"""
if t < duration:
t_matrix = np.matrix([
[0, 0, 0, 0, 0, 1],
[duration ** 5, duration ** 4, duration ** 3, duration ** 2, duration, 1],
[0, 0, 0, 0, 1, 0],
[5 * duration ** 4, 4 * duration ** 3, 3 * duration ** 2, 2 * duration, 1, 0],
[0, 0, 0, 2, 0, 0],
[20 * duration ** 3, 12 * duration ** 2, 6 * duration, 2, 0, 0]
])
x_matrix = np.matrix([[start[i], end[i], 0, 0, 0, 0] for i in range(len(start))]).T
k_matrix = np.linalg.inv(t_matrix) @ x_matrix
time_vector = np.matrix([t ** 5, t ** 4, t ** 3, t ** 2, t, 1]).T
x = (k_matrix.T @ time_vector).T.A[0]
else:
x = end
return x
直线段 + 抛物线过渡 ¶
两段形状相同的抛物线,中间连接的直线段是公切线
- 过渡段:抛物线段
- 直线段:顾名思义
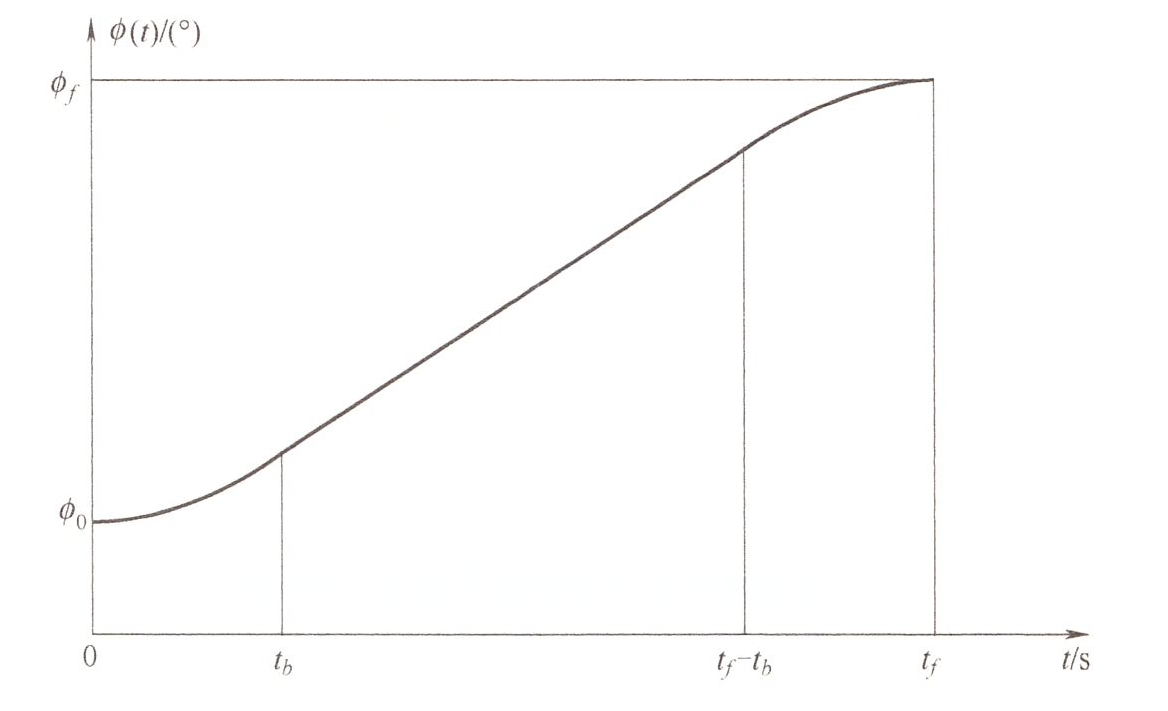
给定:起点 \(\phi_0\)、终点 \(\phi_{final}\)、总时间 \(t_{final}\)、加速度 \(\ddot\phi\) 需要求解:过渡时间(抛物线段)\(t_b\)、速度(直线段)\(k_b\)
过渡段的时间间隔,二次方程求根公式求解。舍掉 + 号的解是因为 \(t_b < t_{f}\)
这里相当于初速度为 0 的平抛
def parabolic_transition(start, end, t, duration):
"""
抛物线过渡插值
:param start: 起始点坐标
:param end: 终点坐标
:param t: 当前时间
:param duration: 总时长
:return: 当前时刻的位置
"""
if t < duration:
tx = t / duration
if t < 0.5 * duration:
tx = 2 * (tx ** 2)
else:
tx = 0.5 + 2 * (tx - 0.5) - 2 * (tx - 0.5) ** 2
x_array = start * (1 - tx) + end * tx
x_angles = inverse_kinematics(x_array)
else:
x_angles = inverse_kinematics(end)
return x_angles
中间点 + 抛物线过渡 ¶
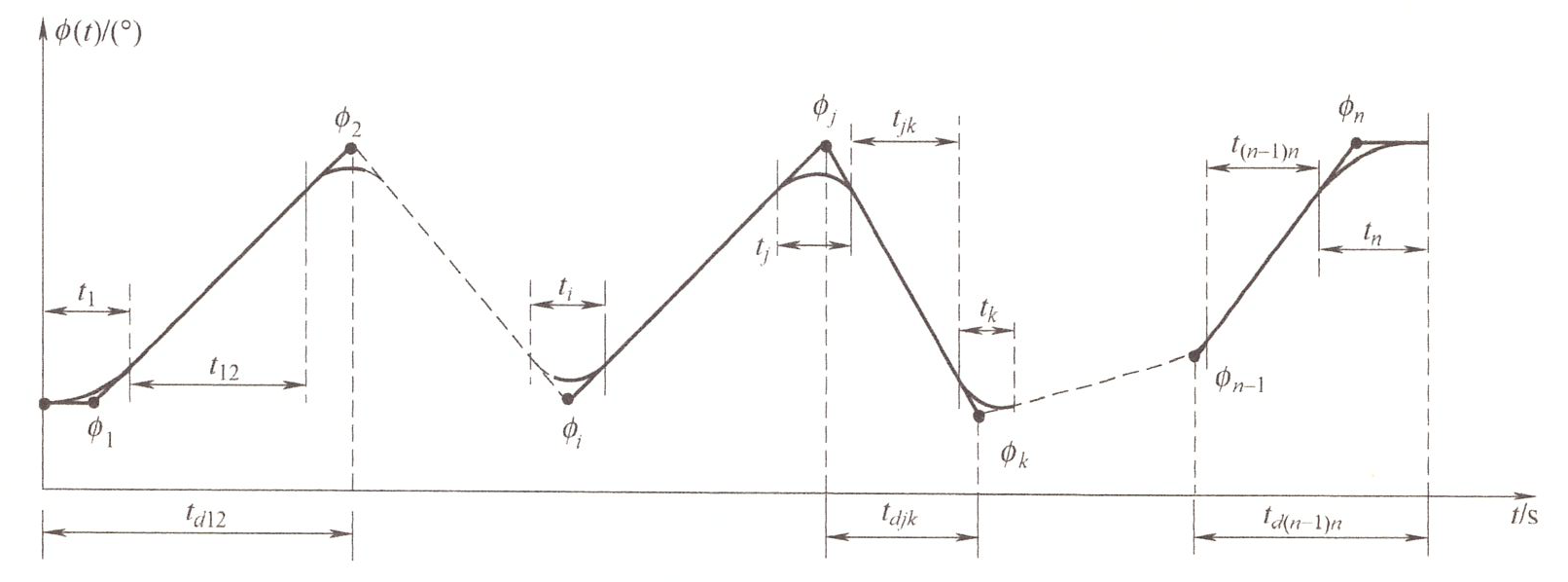
给定: 系列点 \(\phi_0, \phi_1,\dots,\phi_{final}\)、各段时间 \(t_{dij}\)、加速度 \(\ddot\phi\)
需要求解: 各段的速度 \(k_{ij}\),以及过渡段的时间 \(t_{i}\),直线段的时间 \(t_{ij}\)
中间段计算 ¶
过渡段 \( j \) 加速度
过渡段 \( j \) 时间间隔
直线段 \( jk \) 速度
直线段时间 \( jk \) 间隔
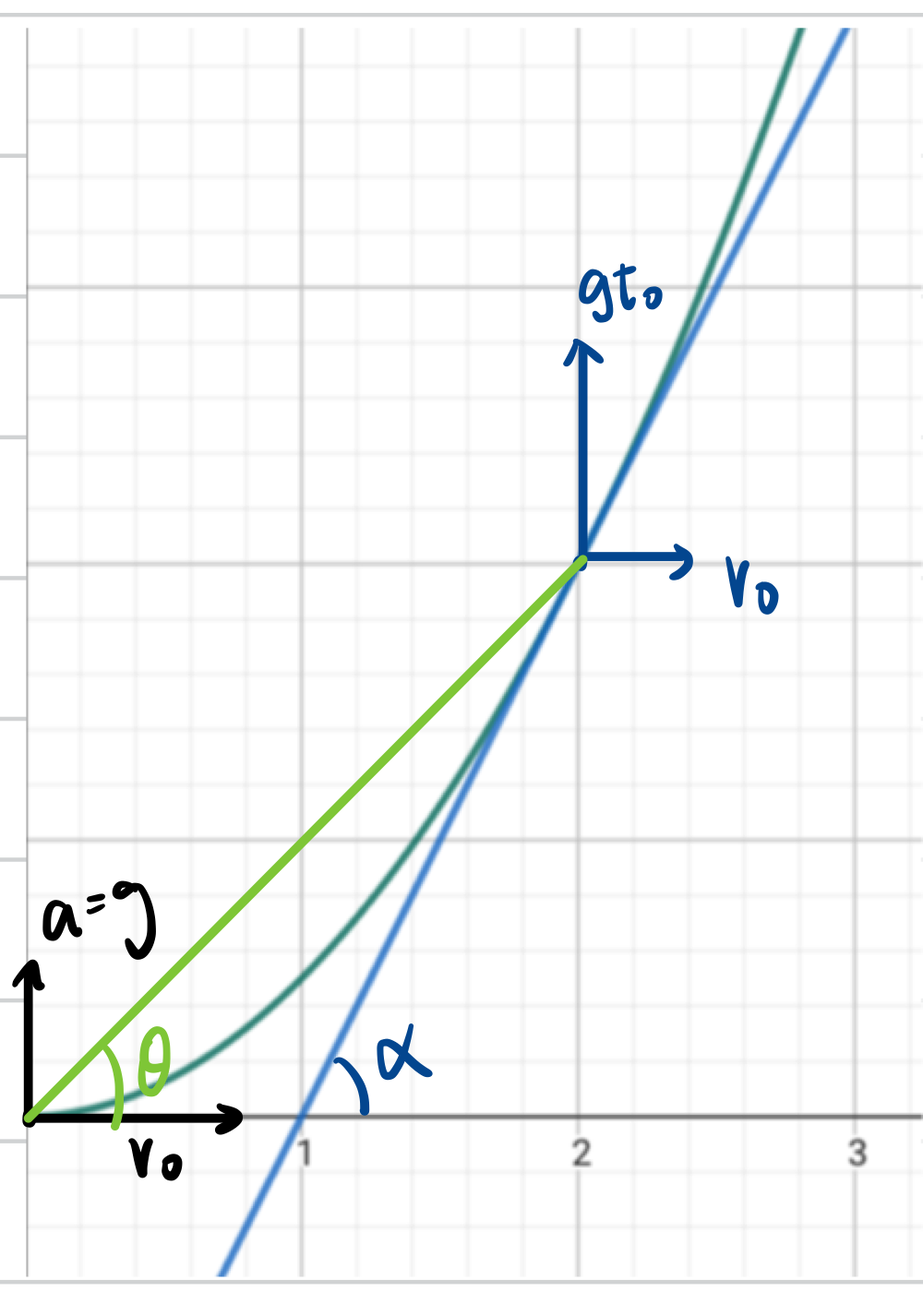
为什么是 \(\frac{1}{2}t\)
这里可以联想到高中平抛运动当中的知识,速度角和位置角有一个 \(\frac{1}{2}\) 的关系。
这个其实很容易推导:
- 速度角:\(\tan \alpha = \frac{v_y}{v_x}= \frac{g\cdot t}{v_0}\)
- 位置角:\(\tan \theta = \frac{y}{x} = \frac{\frac{1}{2}g\cdot t^2}{v_0\cdot t} = \frac{1}{2}\cdot \tan \alpha\)
也就是说,任意给定抛物线上的点,找到位移中点,连线即可得到速度方向
起始段计算 ¶
过渡段 1 加速度
过渡段 1 时间间隔
根据切点速度相等列写方程
求根公式解得:
直线段 12 速度
直线段 12 时间间隔
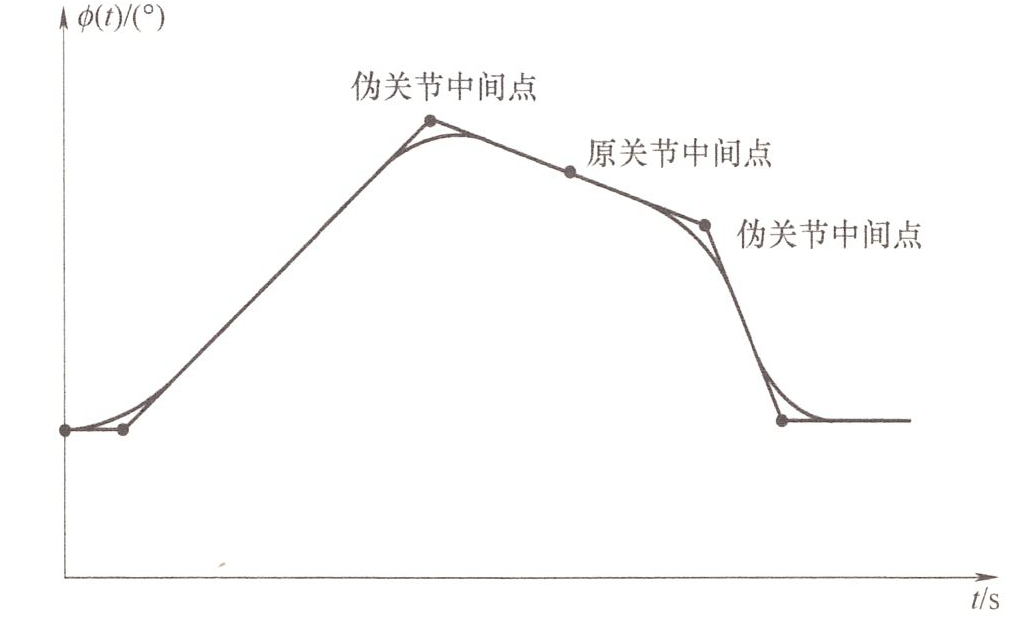
这里因为抛物线对轨迹进行了圆滑处理,相当于先用直线连接起来,再用抛物线做一个圆角,所以并不能真正到达对应的点
解决方案:设置两个伪关节,连线经过给定点,则可以保证经过给定点
笛卡尔空间规划 ¶
旋转矩阵和欧拉角不可以插值的原因:插值得到的 R 矩阵不一定属于 SO(3)
等效轴角插值 ¶
等效轴角的表示:\((\hat{k}_{x},\hat{k}_{y},\hat{k}_{z})^{\mathrm{T}}\) 为等效单位转动轴,\(\theta\) 为绕该轴的转动量(这里单位为 °)
等效轴角表示并不唯一
可以表示围绕空间 \((1,2,3)^{\mathrm{T}}/\sqrt{14}\) 轴旋转 450° 获得的姿态,该最终姿态也等于绕同一轴旋转 \(450°+360°n\) 的结果,这里 \(n\) 为任意整数。
并且注意等效轴角在 \(\theta =0\) 的时候无法表示,所以需要特殊处理。
对两个等效轴角表示的姿态
插值时,通常应该选择使得 \(\left\|\left(\begin{array}{c} k_{0x} \\ k_{0y} \\ k_{0z} \end{array}\right)-(\theta_{1}+360n)\left(\begin{array}{c} \hat{k}_{1x} \\ \hat{k}_{1y} \\ \hat{k}_{1z} \end{array}\right)\right\|\) 最小的 \(n\),然后对 \(\left(\begin{array}{c} k_{0x} \\ k_{0y} \\ k_{0z} \end{array}\right) \text { 和 } \left(\theta_{1}+360n\right)\left(\begin{array}{c} \hat{k}_{1x} \\ \hat{k}_{1y} \\ \hat{k}_{1z} \end{array}\right)\) 运用前面的多项式或带抛物线过渡直线段等插值方法。
代码实现 ¶
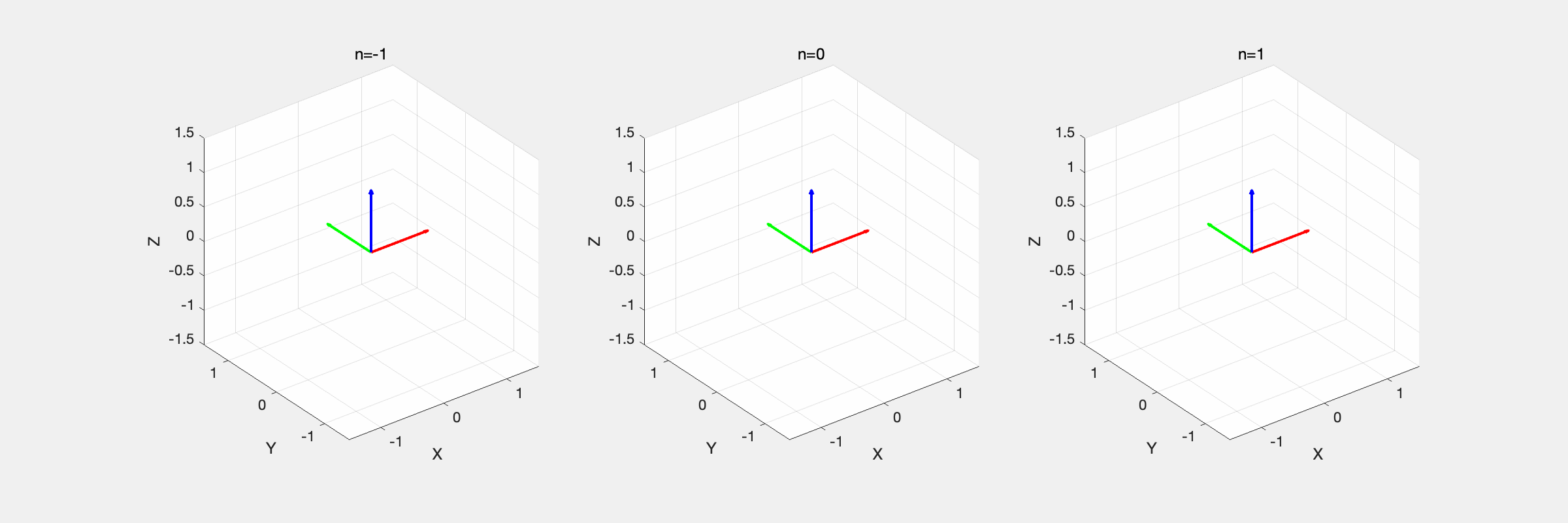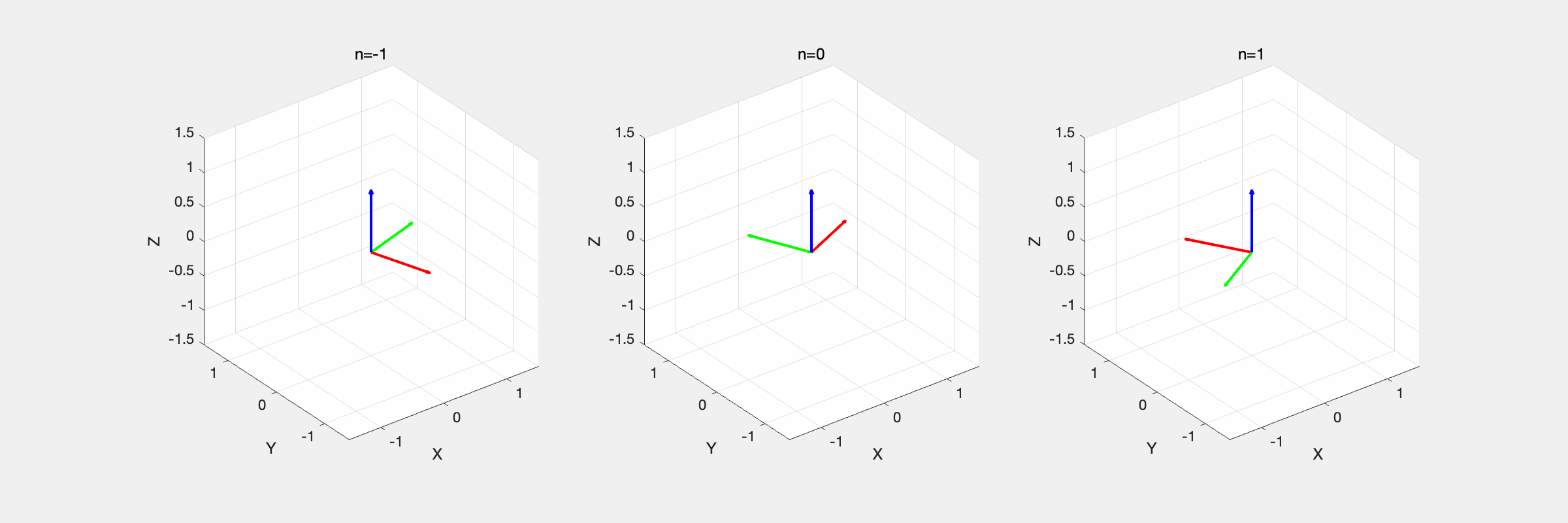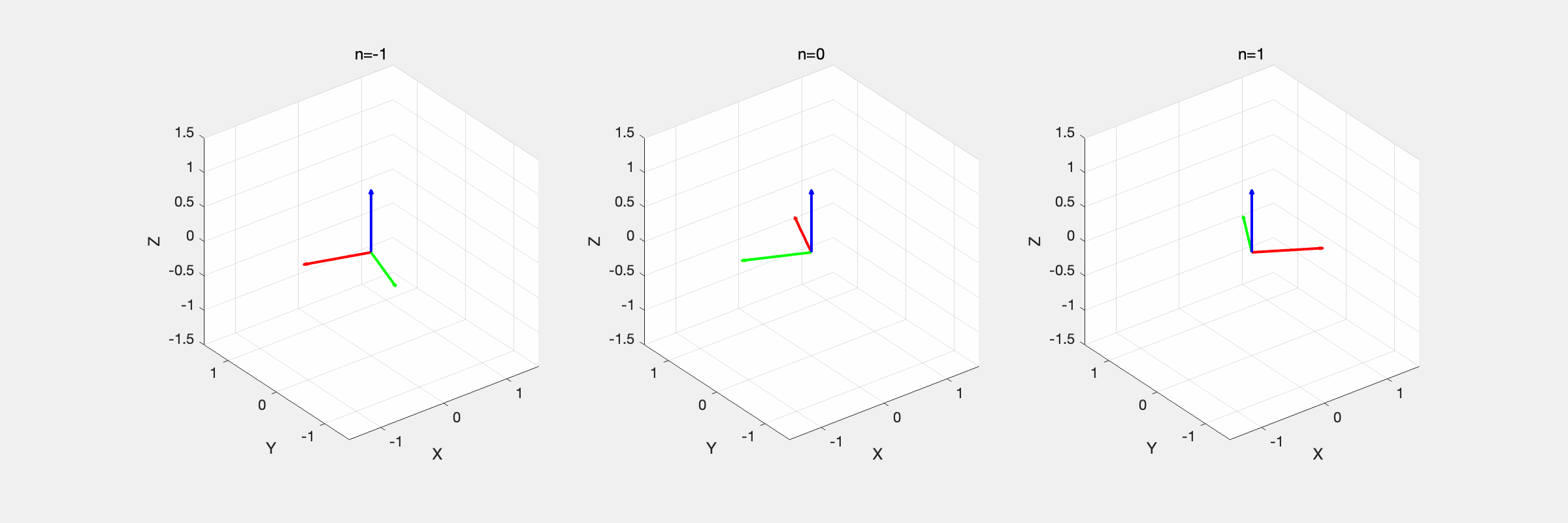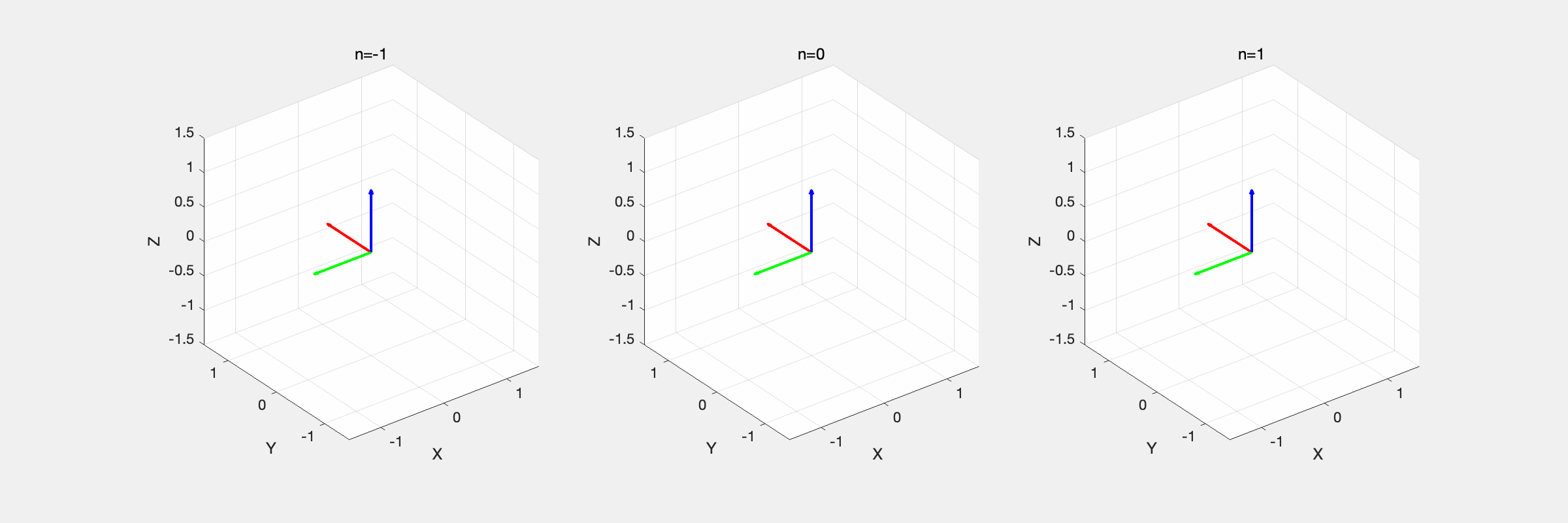
编程实现等效轴角的插值,并比较不同 n 下的结果
clc;clear;
%主程序
%初始姿态示例:绕z轴旋转0和π/2
K0 = [0,0,0]; %初始姿态(无旋转)
n_values = [-1,0,1]; %不同n值测试
% 创建3个子图
figure('Position',[100 100 1200 400]);
subplot_handles = zeros(1,3);
h_x = zeros(1,3);
h_y = zeros(1,3);
h_z = zeros(1,3);
% 初始化3个子图
for j = 1:length(n_values)
subplot_handles(j) = subplot(1,3,j);
hold on;
grid on;
axis equal;
xlabel('X');
ylabel('Y');
zlabel('Z');
view(3);
xlim([-1.5,1.5]);
ylim([-1.5,1.5]);
zlim([-1.5,1.5]);
title(['n=',num2str(n_values(j))]);
% 初始化动画对象
origin = [0;0;0];
h_x(j) = quiver3(origin(1),origin(2),origin(3),1,0,0,'r','LineWidth',2);
h_y(j) = quiver3(origin(1),origin(2),origin(3),0,1,0,'g','LineWidth',2);
h_z(j) = quiver3(origin(1),origin(2),origin(3),0,0,1,'b','LineWidth',2);
end
% 创建动画
while true % 无限循环
for t = 0:0.01:1 % 减小步长从0.02到0.01使动画更慢
for j = 1:length(n_values)
n = n_values(j);
K1 = (pi/2+2*pi*n)*[0,0,1];
%三次多项式插值
kt = K0+(3*t^2-2*t^3)*(K1-K0);
R = rotation_vector_to_matrix(kt);
%更新坐标轴
x_axis = R*[1;0;0];
y_axis = R*[0;1;0];
z_axis = R*[0;0;1];
set(h_x(j),'UData',x_axis(1),'VData',x_axis(2),'WData',x_axis(3));
set(h_y(j),'UData',y_axis(1),'VData',y_axis(2),'WData',y_axis(3));
set(h_z(j),'UData',z_axis(1),'VData',z_axis(2),'WData',z_axis(3));
end
drawnow;
pause(0.02); % 添加暂停使动画更慢
end
end
%旋转向量到旋转矩阵的函数
function R = rotation_vector_to_matrix(k)
% 这个函数实现了罗德里格斯公式,将旋转向量转换为旋转矩阵
% 输入k是旋转向量,包含了旋转轴方向和旋转角度(角度在向量的模长中)
% 1. 计算旋转角度theta(弧度),即旋转向量的模长
theta = norm(k);
% 2. 如果旋转角度为0,直接返回单位矩阵(不旋转)
if theta == 0
R = eye(3);
return;
end
% 3. 计算单位旋转轴向量ne
ne = k/theta; % 归一化得到单位向量
% 4. 构造ne的叉积矩阵K,用于后续计算
% K = [ne]_× 是ne的叉积矩阵,满足K*v = ne × v
K = [0,-ne(3),ne(2);
ne(3),0,-ne(1);
-ne(2),ne(1),0];
% 5. 使用罗德里格斯公式计算旋转矩阵
% R = I + sin(θ)[k]_× + (1-cos(θ))[k]_×^2
% 其中I是单位矩阵,[k]_×是叉积矩阵,θ是旋转角度
R = eye(3) + sin(theta)*K + (1-cos(theta))*(K*K);
end
Slerp | 四元数球面线性插值 ¶
Key Assumption: \(r_t\) 从 \(r_0\) 到 \(r_1\) 匀速旋转
证明方法:线性表出 & 两个欧拉参数内积等于夹角 cos 值
\(S^3\) 中的单位四元数 \(\eta + i\varepsilon_1 + j\varepsilon_2 + k\varepsilon_3\) 与 \(\mathrm{U}\) 中的欧拉参数 \((\eta, \varepsilon_1, \varepsilon_2, \varepsilon_3)^T\) 一一对应。考虑两个用欧拉参数(等价于用单位四元数)表示的不同姿态:
式中,\(\mathbf{r}_0 \neq \mathbf{r}_1\) 且 \(\mathbf{r}_0 \neq -\mathbf{r}_1\)。四元数插值的目的是找出中间姿态 \(\mathbf{r}_t\),\(t \in [0, 1]\)(注意这里的起止时间作了归一化
注意到 \(\|\mathbf{r}_0\| = \|\mathbf{r}_1\| = 1\)。
于是,两个欧拉参数的内积等于它们夹角的余弦值
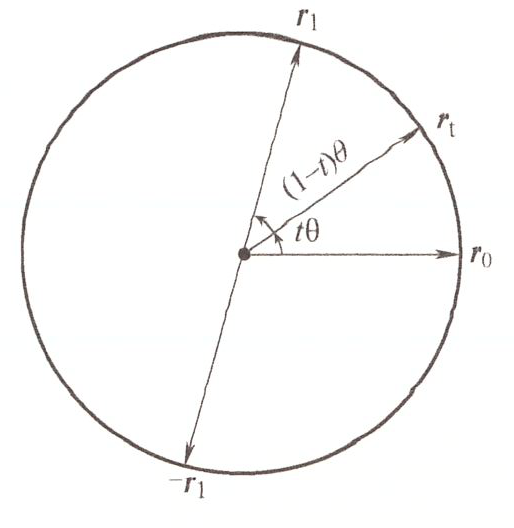
如图所示,将中间姿态 \(\mathbf{r}_t\) 限制在 \(\mathbf{r}_0\) 和 \(\mathbf{r}_1\) 确定的平面中并假设匀速旋转,可以使四元数插值问题化为一个简单的平面几何问题:\(\mathbf{r}_0\)、\(\mathbf{r}_1\) 和 \(\mathbf{r}_t\) 都在平面单位圆上,\(\mathbf{r}_t\) 从 \(\mathbf{r}_0\) 匀速旋转到 \(\mathbf{r}_1\)。
由于匀速旋转,对于 \(t \in [0, 1]\),\(\mathbf{r}_0\) 与 \(\mathbf{r}_t\) 的夹角是 \(t\theta\),\(\mathbf{r}_1\) 与 \(\mathbf{r}_t\) 的夹角是 \((1-t)\theta\),则由欧拉参数内积与夹角余弦值的关系,有
同时,\(\mathbf{r}_t\) 可以表示为 \(\mathbf{r}_0\) 和 \(\mathbf{r}_1\) 的线性组合,即
最后,求解线性方程组
联立两式,可求得
式中,\(\theta = \cos^{-1}(\mathbf{r}_0 \cdot \mathbf{r}_1)\)。
注意到单位四元数 \(r\) 和 -\(r\) 表示三维空间中的同一姿态。一般应该选取最短路径进行球面线性插值。
因此如果两四元数的夹角为钝角,则可通过将其中一个四元数取负,再对得到的两个夹角为锐角的四元数进行球面线性插值。
初始两个四元数如果是 \(\pi\) 的话,就说明两个四元数对应的是同一个姿态。
如果
代码实现 ¶
def slerp(q1, q2, t):
"""
球面线性插值(Slerp)
:param q1: 起始四元数
:param q2: 终止四元数
:param t: 插值因子,范围 [0, 1]
:return: 插值后的四元数
"""
dot_product = np.dot(q1, q2)
dot_product = np.clip(dot_product, -1.0, 1.0)
theta_0 = np.arccos(dot_product)
sin_theta_0 = np.sin(theta_0)
if sin_theta_0 < 1e-6:
return q1
theta = theta_0 * t
s1 = np.sin(theta) / sin_theta_0
s0 = np.cos(theta) - dot_product * s1
return s0 * q1 + s1 * q2
需要下载 matlab 的 robotics toolbox 和
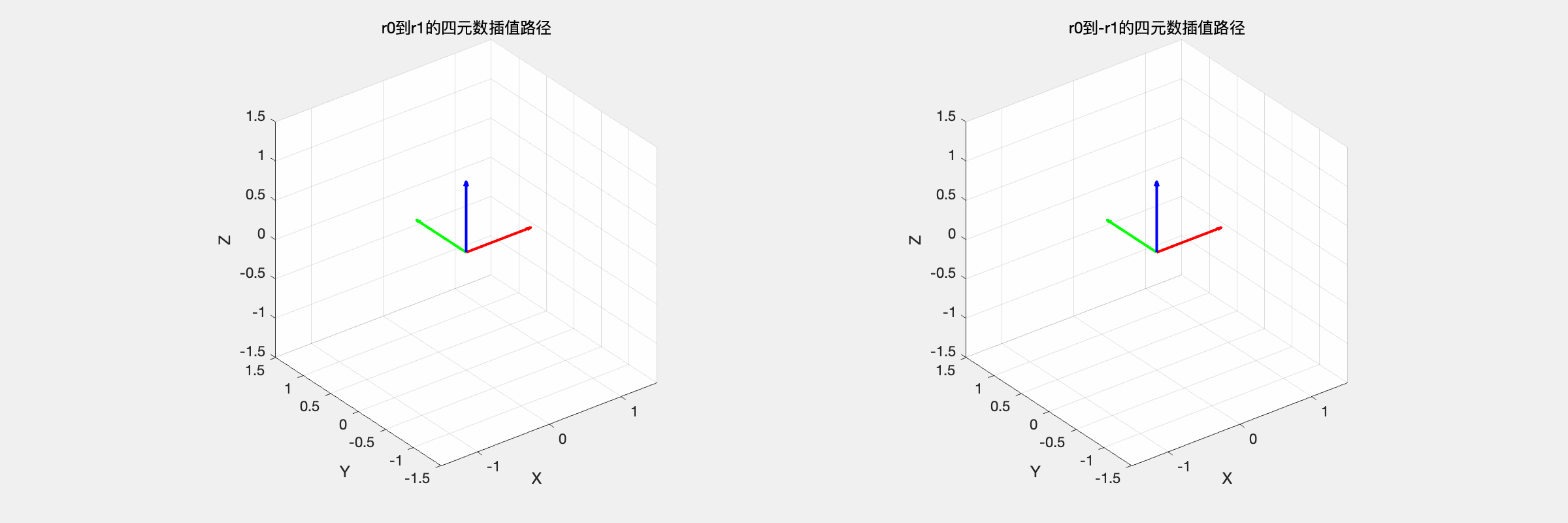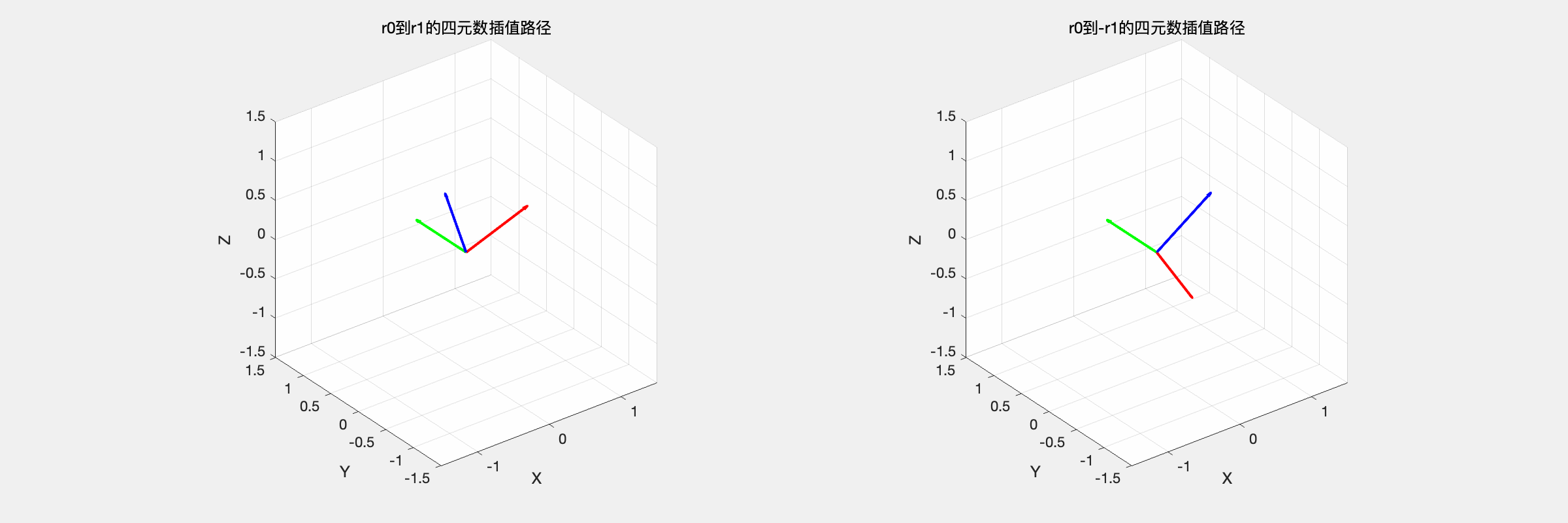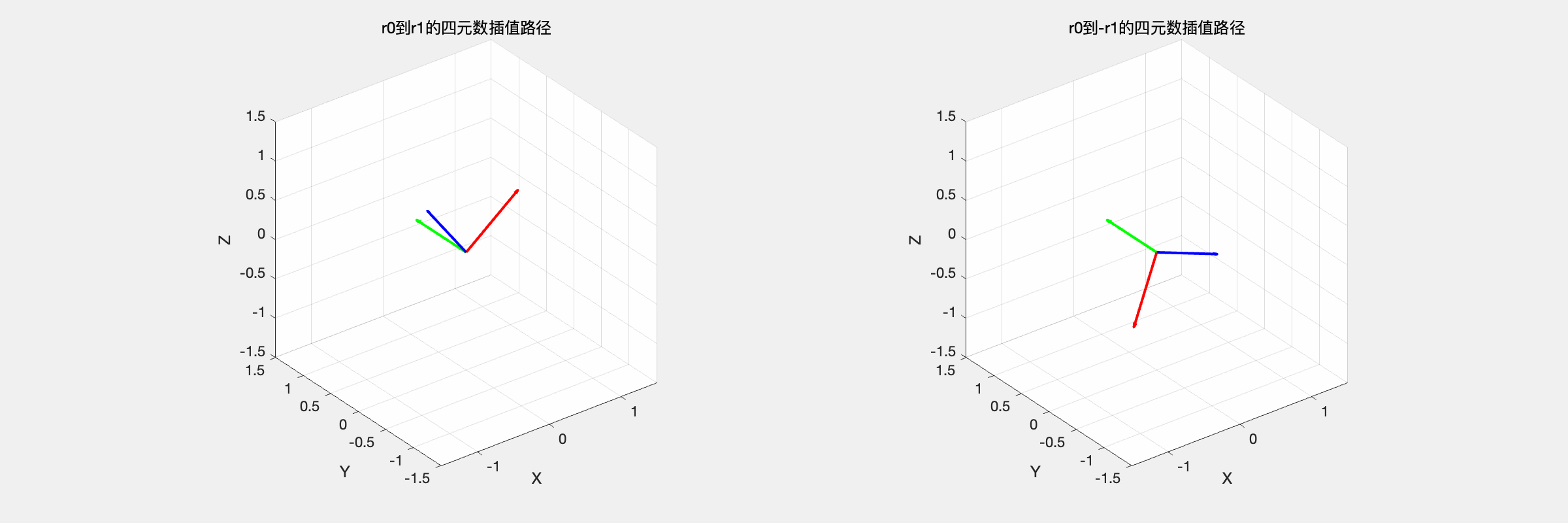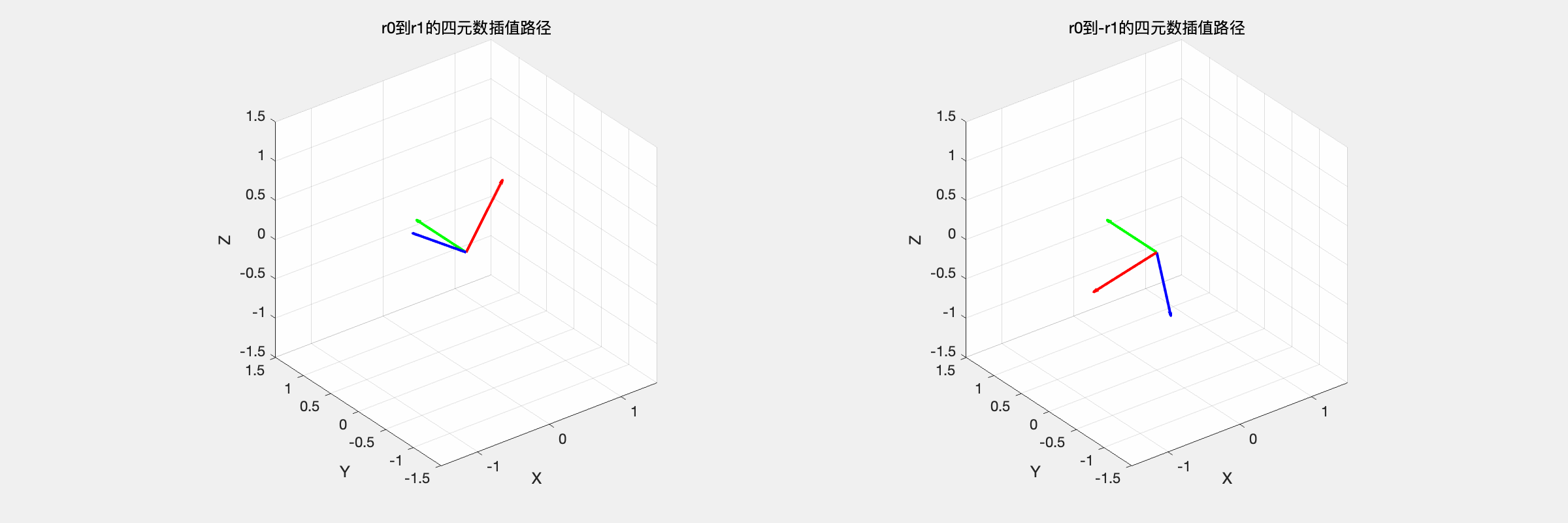
| slerp_interpolation,r0 到 r1 和 r0 到 -r1 的对比 | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 | |
Slerp 拓展:对角速度有约束 ¶
这个题目与变式历年卷考察多次,一定要掌握
当匀速旋转的假设不成立的时候,需要应用多项式规划
由于单位四元数球面线性插值方法 (Slerp) 的旋转角速度是定值, 此时直接应用 Slerp 公式进行规划是不行的。结合 Slerp 公式,给出上述要求下相应的姿态
若单位四元数插值时,要求在初始姿态 \(r_0\) 和最终姿态 \(r_1\) 时的角速度均为 \(0\), 且转动过程中角速度连续。
解答
设 \(r_0\) 与 \(r_1\) 的夹角为 \(\theta\),\(r_0\) 与 \(r_t\) 的夹角为 \(\beta\), 令 \(\beta = x(t)\theta\),\(t \in [0,1]\)
不妨假设 \(x(t) = a_1t^3 + a_2t^2 + a_3t + a_4\)
即 \(x(t) = -2t^3 + 3t^2\)
令 \(r_t = k_0r_0 + k_1r_1\),有
即
题型 ¶
解方程比较麻烦
多项式参数计算:时间、速度 ¶


抛物线过渡计算 ¶


已知起点角度为 138°,中间点到达的点角度为 158°,时间为 5.5s,点角度为 10°,时间为 31.5s。需要计算中间点。中间点关于中点对称。采用带有抛物线过渡的线性规划来实现。过渡段(第二个中间点到第三个中间点)的持续时间为 16s。
matlab 求解方程 ¶
- 方程写出来,丢给 gpt