LQR 控制 ¶
约 270 个字 预计阅读时间 1 分钟
更加看重收敛速度,在 Q 上面做文章。更加看重输入的值的话,就在 R 上面做文章
对于一个线性时不变系统,其状态方程可以表示为:
\[\dot{x} = Ax + Bu\]
LQR 的 cost function 可以表示为:
\[
J = \int_{t_0}^{t_f} \left( \mathbf{x}^T \mathbf{Q} \mathbf{x} + \mathbf{u}^T \mathbf{R} \mathbf{u} \right) dt
\]
cost function
Q: 表达的是因为系统变化而造成的能量损耗
权重矩阵 \(Q\) 和 \(R\) 用于调整系统状态和控制输入在 cost function 中的
相对重要性。
LQR 的目标是找到一个控制策略 \(u^*(x)\),使得对于任意的初始状态 \(x_0\),cost function \(J\) 都达到最小值。这可以通过求解一个优化问题来实现,其中控制输入 \(u\) 是优化变量,cost function \(J\) 是优化目标。
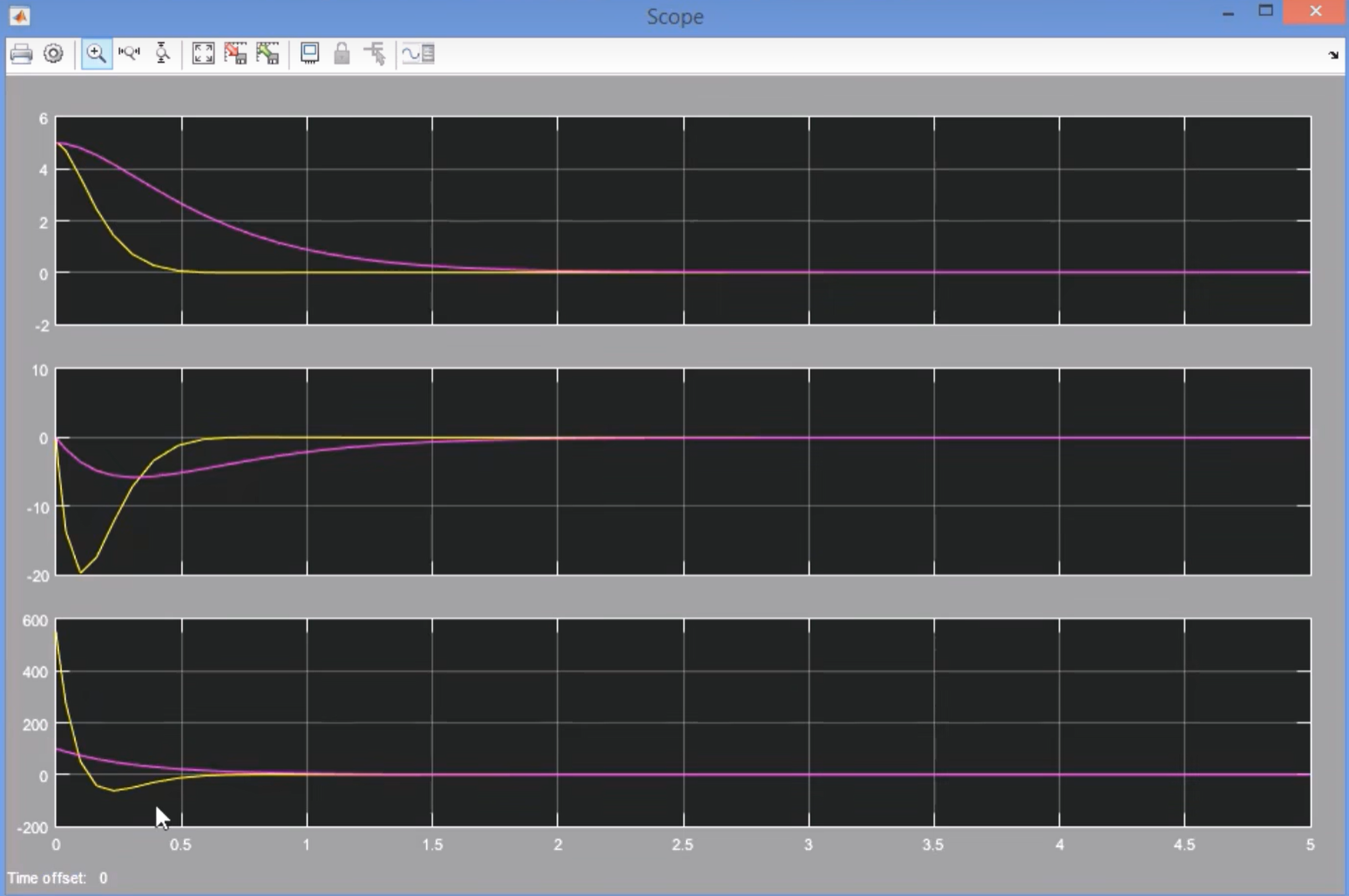
如图,黄线是选用较大的 Q,可以看到快速收敛但是输入值较大;紫线是选用较大的 R,可以看到输入值较小,但是收敛速度较慢。