智能控制技术 ¶

约 5289 个字 1 行代码预计阅读时间 21 分钟

课程介绍

=== " 简介 " - 一般不依据数学模型进行处理。
- 根据积累的经验和知识进行在线推理，确定控制策略。
- 在 精度和不确定性 之间折中
- === "知识框架"

=== " 作业 " 递阶控制、专家控制、模糊控制和神经网络控制各有一个小作业
最后期末会有一个大作业，必须包含模糊控制和神经网络控制。

=== " 智云录像 "

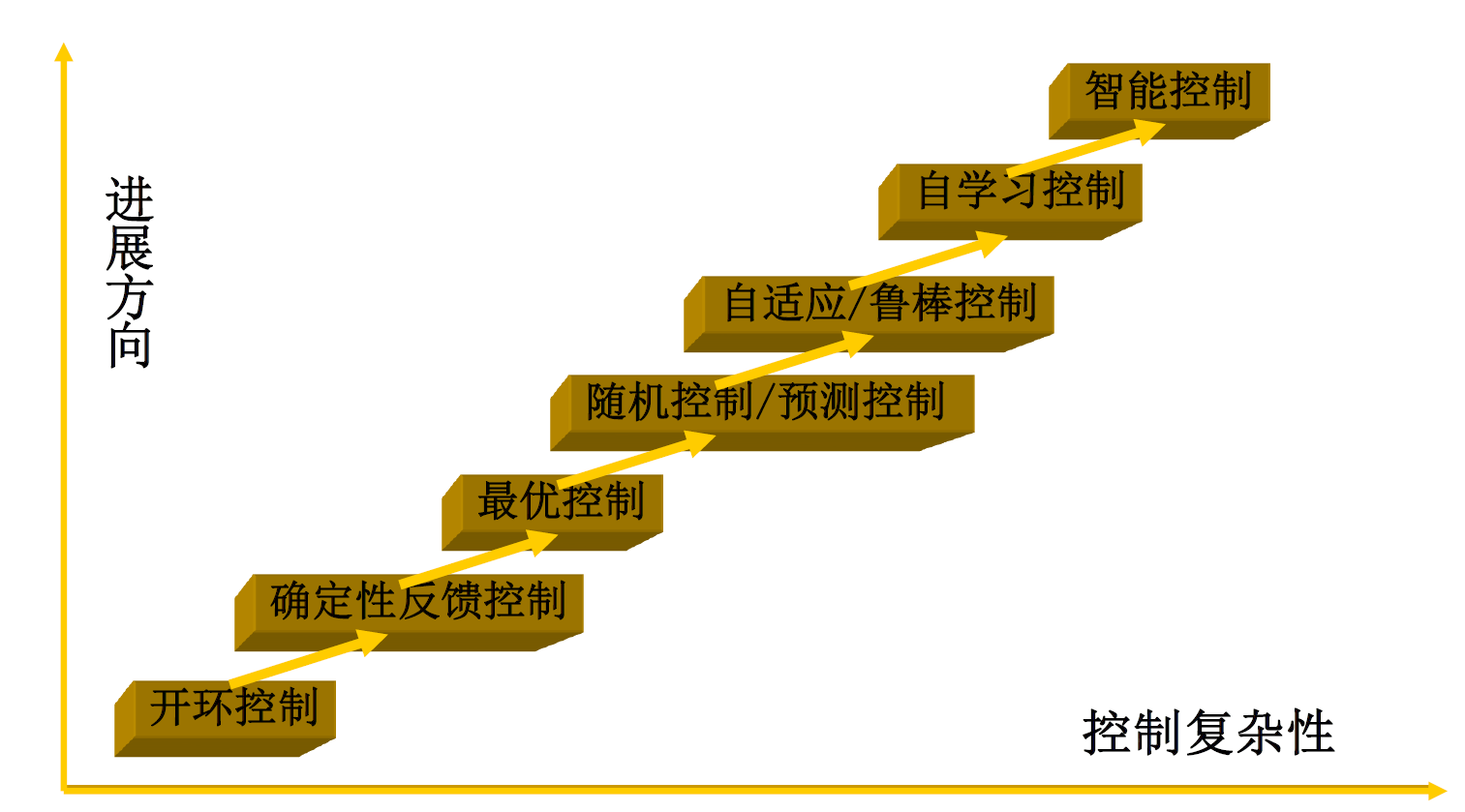
控制学科三大任务：建模、控制、优化

	第一阶段	第二阶段	第三阶段
形成时间	40—50 年代	60—70 年代	80 年代以来
理论基础	经典控制理论	现代控制理论	智能控制理论
研究对象	单入单出系统	多入多出系统	多级多变量系统
分析方法	传递函数频域法	状态方程时域法	多学科交叉
研究重点	反馈控制	最优、随机、自适应控制	不确定、大系统智能控制
控制装置	自动调节器	数字计算机	智能机器
应用	单机自动化	机组自动化	综合自动化

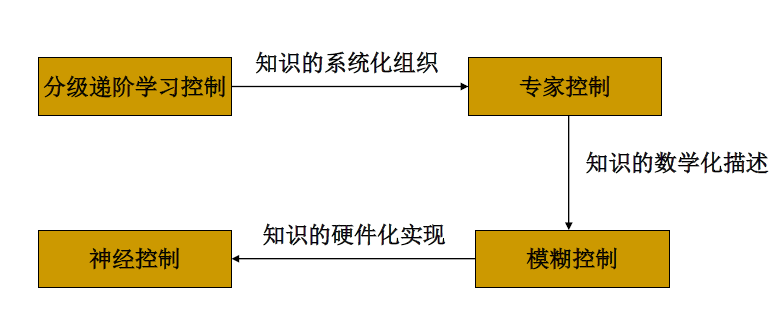
规则驱动：专家系统
数据驱动：神经网络

递阶控制 | Hierarchical Control ¶

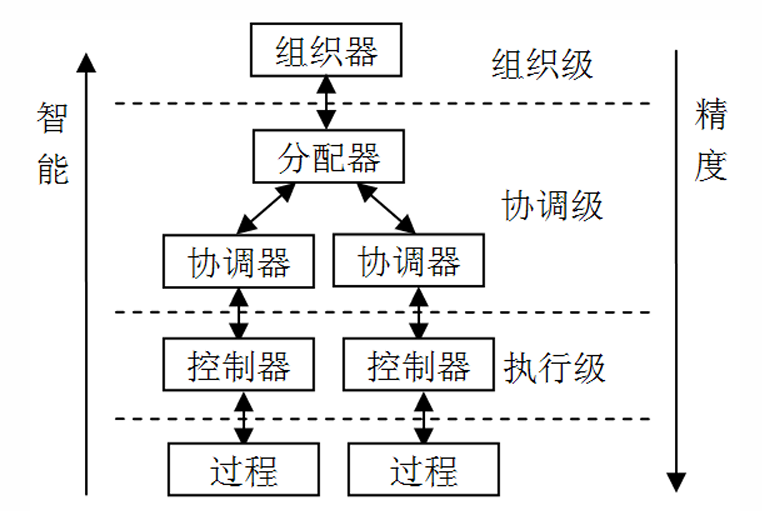
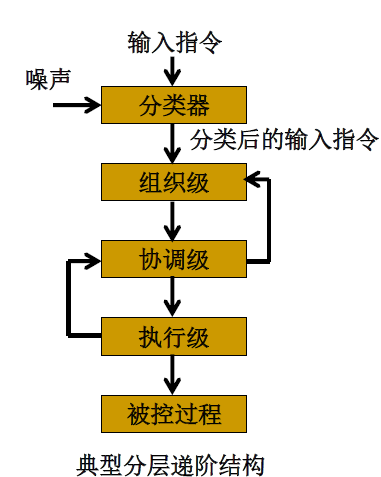
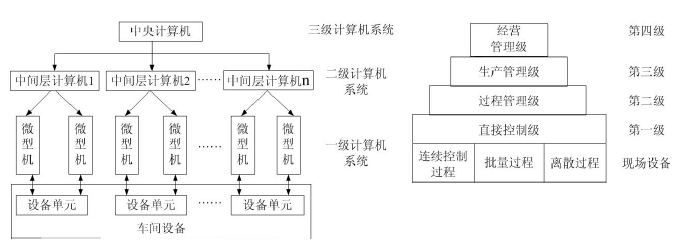
分级递阶的控制结构成为智能控制的一种典型结构。

三级递阶智能控制系统由组织级、协调级和执行级组成。

在实际应用中，往往采用不同的基于知识的表示和搜索推理技术的组合，这些技术包括状态空间、与或图、谓词逻辑、语义网络、模糊集合、Petri 网、规则、过程、黑板和神经网络等。

各级按“精度递增伴随智能递减”的原则进行设计。

递阶智能控制是基于信息论的智能控制系统。

原理与结构 ¶

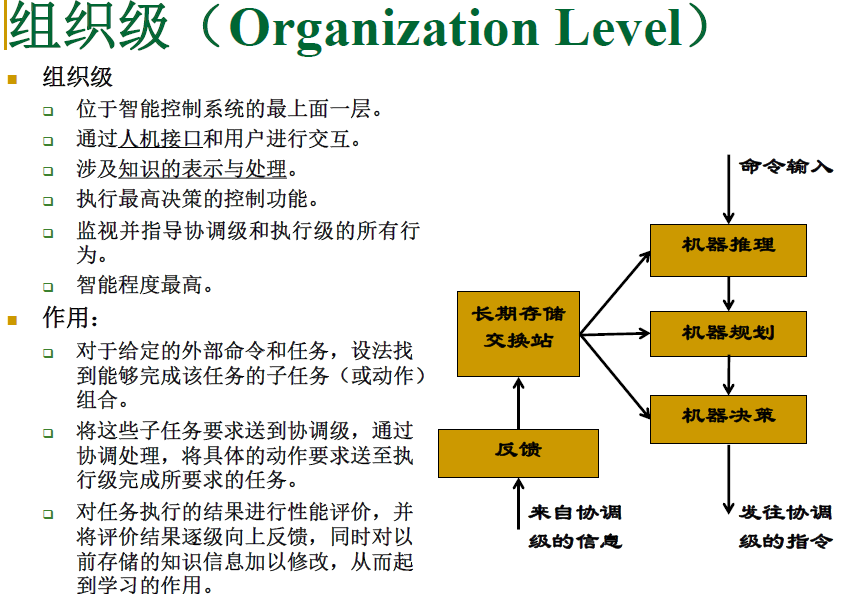
第一级：组织级

代表系统的主导思想，人工智能起控制作用。

组织级为决策控制级，其接受控制期望目标和协调级反馈信息，制定最优决策，对协调级下达决策指令。

推理，规划，决策，记忆，数据存取

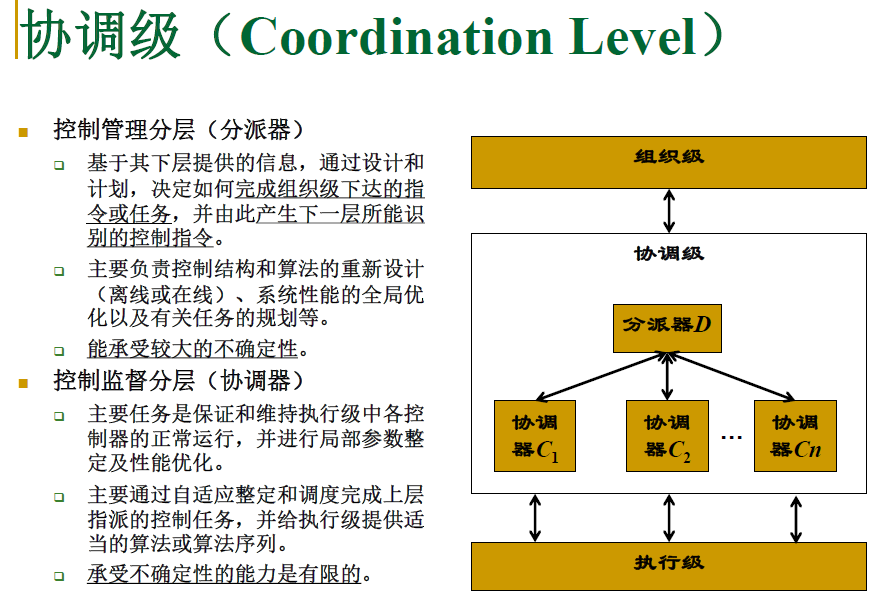
第二级：协调级

上（第一级）下（第三级）级间的接口，由人工智能和运筹学起控制作用。

其接受组织级的决策指令，协调和优化执行级各控制器的设定值，并向组织级传送执行结果信息；

第三级：执行级

智能控制系统的最低层级，要求具有很高的精度，并由控制理论进行控制。

执行级为直接控制级，其各个控制器分别控制被控对象的一部分；

多级多目标结构

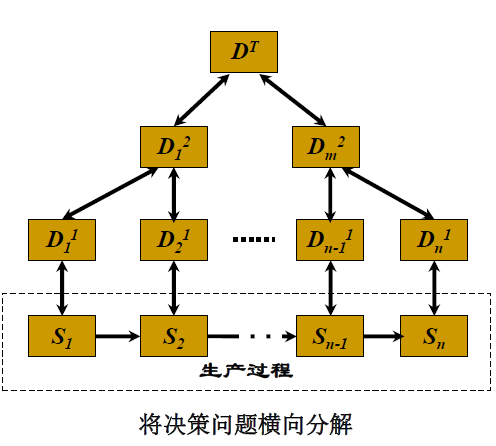
系统组成：系统由若干个可分的、相互关联的子系统组成。
决策单元排列：所有决策单元按一定支配关系递阶排列。
上下级关系：同一级各单元要受上一级的干预。同时又对下一级决策单元施加影响。
信息交换：同级之间不交换信息。上下级间交换信息。
目标协调：同一级决策单元如有相互冲突的决策目标，由上一级决策单元加以协调。
总目标：协调的总目标是使全局达到优化或近似优化。
结构形式：多级多目标决策单元在不同级间递阶排列，形成了金字塔式结构。

信息论 ¶

对系统的各级均采用熵（信息熵，Shannon 熵）作为描述和度量系统控制作用的测度。

熵（Entropy, H）

在信息论中指的是信息源中所包含的平均信息量

\[ H = -k \sum_{i=1}^{n} P_i \ln P_i \]

其中，$P_i$ 为信息源中各事件发生的概率。

机器知识 K 可表示为

\[ K = -\alpha - \ln p(K) \]

知识流量 R是智能机器的主要变量，在一有限时间间隔 T 上为

\[ R = K/T \]

机器智能 MI、事件数据库 DB 与知识流量 R 之间满足关系

\[ (MI):(DB) \rightarrow (R) \]

- 若知识流量不变，增大数据库DB的熵将减少机器智能MI的熵。 - 知识流R在信息理论意义上代表系统的工作能力。 - 建立和执行任务期间，知识流量一般不变。

IPDI 原理：

精度递增伴随智能递减 (Increasing precision with decreasing intelligence)

原理适用于递阶系统的单个层级和多个层级。

分层递阶 ¶

递阶智能控制的实质

在结构上遵循精度随智能降低而提高（ IPDI ）的原理，寻求系统的正确决策与控制序列，能够使系统的总熵为最小。

智能机器人控制系统

学习级（组织级） 基于专家系统、识别、规划

技能级（协调级） 神经模糊网络、为学习级形成的控制策略生成合适的控制参考信号。

适应级（执行级） 神经网络、作为机器人的控制器以适应技能级生成的控制参考信号。

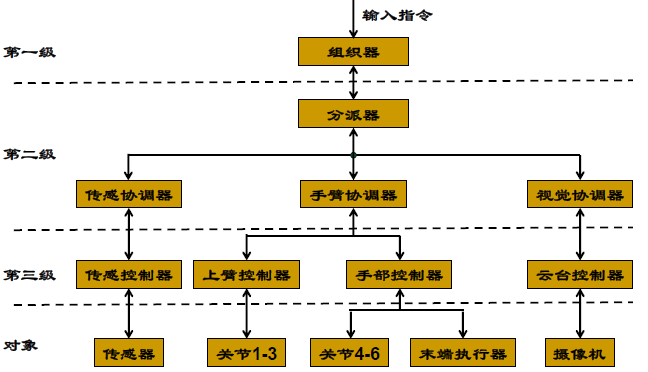
协调级：Petri 网翻译器；语言决策树组织级：Boltzmann机；语言决策树；自动机

集散控制系统 ¶

集散控制系统的特点： - 分级递阶控制 - 分散控制 - 自治性与协调性

HW01- 递阶控制 ¶

如图所示的多机器人协作系统由三个机器人组成，分别为两个悬挂移动式多关节机器人（SMR1 和 SMR2）和一个地面移动式多关节机器人（GMR）。

SMR1 和 SMR2 的主体是两个七关节式机器人，悬挂在一个固定在顶部的方形托架上，它们的移动支架都能够沿着悬挂导轨在方形托架的允许范围内移动。GMR 的主体是六关节式机器人 HP3，安装在一个轮式移动基座 PowerBot 上，能够在地面上随意移动。

系统配置三级视觉系统，第一级为全局的外部三维点云相机，第二级为装在机械臂腕部的深度相机，第三级为装在机械臂手抓中心的摄像头。各机械臂均配备力矩传感器。

SMR1、SMR2 和 GMR 都有自己独立的控制计算机，系统中另有一台独立的计算机 TAC，各计算机之间通过无线通讯连接，实现数据交互。

系统的目标任务是：从无序堆放的工件中拾取目标螺杆，并将螺杆的两端装上合适的螺帽，然后放置在期望目标位置。

请根据以上各部分的具体任务和功能，采用递阶控制的思想将多机器人协作系统进行分解，并画出该递阶控制系统的分级系统结构图。

专家控制 | Expert Control ¶

概念 ¶

应用专家系统概念和技术，模拟人类专家的控制知识与经验而建造的控制系统，称为专家控制系统。

专家系统的基本功能取决于它所含有的知识，因此，专家系统称为基于知识的系统（ knowledge based system ）

结构、类型与设计 ¶

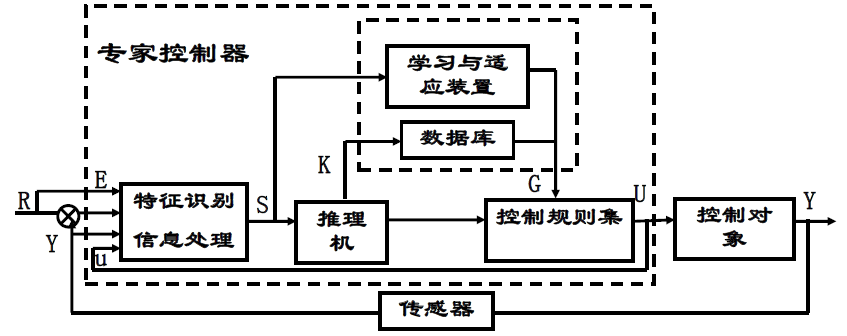
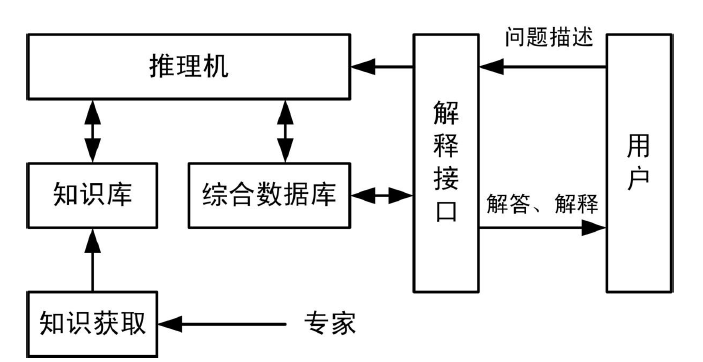
知识库：
- 存储专家系统的专门知识，包括事实、可行操作和规则等。
推理机：
- 解释程序：能够根据知识进行推理和导出结论，而不是简单地搜索现成的答案。
- 调度程序：用于记忆所采用的规则和控制策略的程序，使整个专家系统能够以逻辑方式协调地工作。
综合数据库：
- 又称全局数据库或总数据库，用于存储领域或问题的初始数据和推理过程中得到的中间数据（信息），即被处理对象的一些当前事实。
解释接口：
- 能够使系统与用户进行对话的接口，使用户能够输入数据和提出问题并获得答案，了解推理过程。

专家系统将知识组织成三级：数据、知识库、控制

专家 PID 控制 ¶

应用 ¶

HW02- 专家控制 ¶

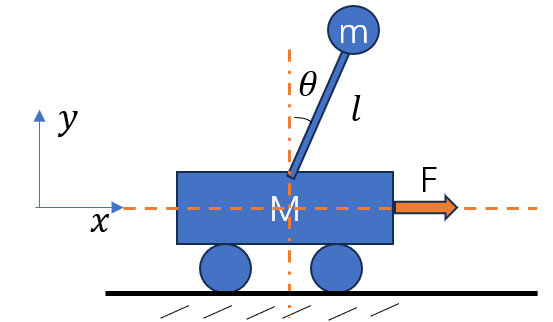
如图所示为车载倒立摆系统，一辆小车在水平轨道上移动，小车上有一个可绕固定点转动的倒立摆。控制小车在水平方向的移动可使摆杆维持直立不倒，这和手掌移动可使直立木棒不倒的现象类似。 d 忽略车轮与地面的摩擦力等阻力，可推导出车载倒立摆的动力学方程如下：

\[ \begin{cases} (M + m) \ddot{x} + m l (\ddot{\theta} \cos \theta + ml \dot{\theta}^2 \sin \theta) = F \\ ml^2 \ddot{\theta} + ml \ddot{x} \cos \theta - mgl \sin \theta = 0 \end{cases} \]

其中的参数如表所示：

参数	大小
摆杆质量 $m$	0.5kg
小车质量 $M$	1kg
摆杆转动轴心到摆杆质心的长度 $l$	0.5m
摆杆与垂直向上方向的夹角 $\theta$	$[0, \pi]$ rad
重力加速度 $g$	9.8m/s²
施加在小车上的水平外力 $F$	$[-F_m, F_m]$ N
小车在水平方向的位移 $x$	不限制

增量型离散 PID 控制算法如下：

\[ F(k) = F(k-1) + K \left[ K_p \Delta \theta (k) + \frac{T}{T_i} \theta (k) + \frac{T}{T_d} (\Delta \theta (k) - \Delta \theta (k-1)) \right] \]

其中 $T$ 为采样时间，$\Delta \theta (k) = \theta (k) - \theta (k-1)$

若 $F_m = 25$，取 $T = 0.0001s$，$K_p = 200$，$K_i = 3$，$K_d = 10$

设计 $0 < \theta_1 < \theta_2 < \theta_m$，$0 < K_s < 1 < K_b$

在离散 PID 控制基础上，采用专家 PID 控制方案，规则如下：

若 $|\theta (k)| \geq \theta_m$ 时，则 $F(k) = \text{sgn}(\theta) F_m$
若 $\theta_2 \leq |\theta (k)| < \theta_m$ 时， 1. 若 $\theta (k) \Delta \theta (k) > 0$ 时，则 $K = K_b$ 2. 若 $\theta (k) \Delta \theta (k) < 0$ 时， a. 若 $\Delta \theta (k) \Delta \theta (k-1) > 0$ 时，则 $K = 1$ b. 若 $\Delta \theta (k) \Delta \theta (k-1) < 0$ 时，则 $K = K_b$
若 $\theta_1 \leq |\theta (k)| < \theta_2$ 时， 1. 若 $\theta (k) \Delta \theta (k) > 0$ 时，则 $K = 1$ 2. 若 $\theta (k) \Delta \theta (k) < 0$ 时， a. 若 $\Delta \theta (k) \Delta \theta (k-1) > 0$ 时，则 $K = K_s$ b. 若 $\Delta \theta (k) \Delta \theta (k-1) < 0$ 时，则 $K = 1$
若 $|\theta (k)| < \theta_1$ 时，则 $K = 1$

若小车和摆杆静止，摆杆与垂直向上方向的初始夹角 $\theta(0) = \frac{\pi}{4} \text{ rad}$，请：

给出上述专家 PID 控制方案的合适参数 $\theta_1, \theta_2, \theta_m$ 和 $K_s, K_b$，通过调节 $F$ 使倒立摆的摆杆夹角 $\theta$ 恢复并维持在期望值（$\theta_d = 0$），在 matlab 中进行仿真，给出位移 $x$、夹角 $\theta$ 和水平力 $F$ 的变化曲线，并比较专家 PID 控制与常规 PID 控制的结果（可尝试参数 $\theta_1 = 0.1, \theta_2 = 0.3, \theta_m = 0.5$ 和 $K_s = 1, K_b = 1.3$）。
针对不同的初始夹角 $\theta(0)$，给出专家 PID 控制的结果。（可能需要调整相关参数 $\theta_1, \theta_2, \theta_m$ 和 $K_s, K_b$）

模糊控制 | Fuzzy Control ¶

a fuzzy inference system is a form of artificial intelligence

fuzzy logic is a way to encode this experience-based knowledge

根据已有的知识设计一种规则

有点像神经网络最后一层的 softmax 输出

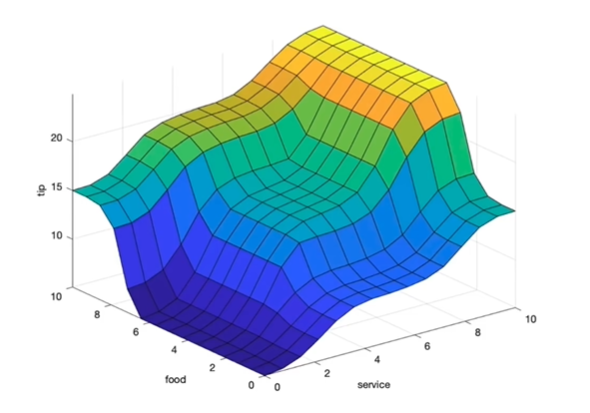
crisp input -> fuzzifizcation -> fuzzy variable -> fuzzy rule -> defuzzification -> crisp output 示例图片——小费与食物、服务的关系

优点：我们一开始不知道规则，但是可以通过数据来学习规则，就像训练神经网络一样，最后可以得到一个可解释性强的模型

数学基础 ¶

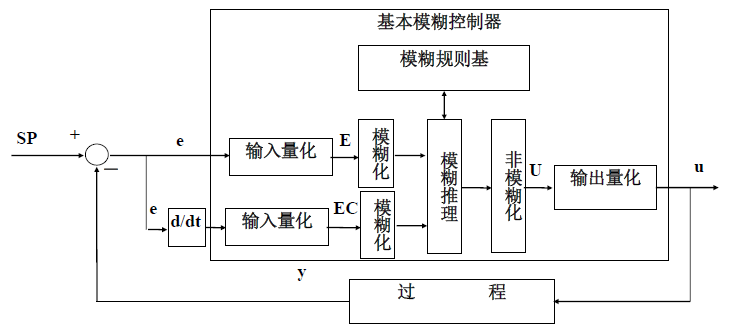
原理与结构 ¶

在被控制对象的模糊模型的基础上运用模糊控制器近似推理手段实现系统控制。

模糊模型是用模糊语言和规则描述的一个系统的动态特性及性能指标。

merbership function¶

隶属函数，需要通过经验和专家知识来确定

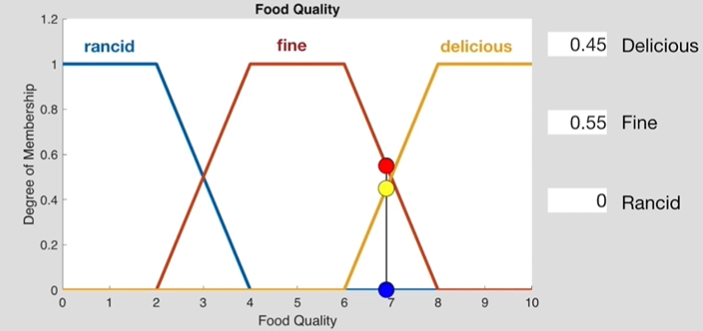把人们语言中or行动中的不确定的量，转换成拥有置信度的模糊变量（input）

fuzzy rules¶

我们需要建立模糊规则，来将模糊变量转换成模糊输出

比如：如果食物好吃，服务好，小费就多；把食物质量和服务态度这两个模糊变量转换成了小费这个模糊变量

fuzzy operators¶

and（min）
or（max）
not（1-a）

T-norm

defuzzification¶

每个规则在推断时候得出来的值含义是规则触发的强度

可以用来判定

最低输出是最小的隶属函数的质心，同样的，最大的输出是最大的隶属函数的质心

所以如果要控制输出量的值域，久需要调整隶属函数

gensurf

只用控制平面查表计算速度很快，但是内部的规则逻辑就不可见了

应用示例 ¶

作为控制器 ¶

汽车侧方停车
倒立摆
人工胰腺

作为决策系统 ¶

金融：贷款风险
医疗：诊断
农业：病虫害诊断

数据驱动 ¶

which parameters are we tuning?¶

使用经验来确定大部分的参数，使用数据来确定剩下的参数

how to tune them?¶

遗传算法

随机取样：去除高损失，保留地损失

一方面，构建模糊控制树更优良，因为一方面参数更少，另一方面，模糊规则更少

训练的思路：先使用数据训练，然后使用获得的知识，对网络的参数进行调整，然后再进行训练

HW03- 模糊控制 ¶

系统方程：

\[ F - G = m \frac{d^2 X}{dt^2} \]

其中，$F$ 为电磁吸力，$m$ 为钢球的质量，重力 $G = mg$，$g$ 为重力加速度。

电磁力方程：

\[ F = K \left( \frac{I}{X} \right)^2 \]

其中，$K$ 为电磁力系数。

电磁线圈方程：

\[ U - K \frac{I}{X} \frac{dX}{dt} = L \frac{dI}{dt} + IR \]

其中，$U$ 为控制电压，$L$ 为电感，$R$ 为线圈电阻。

假定系统参数如下表所示

参数	值
$m$	0.05kg
$g$	9.81m/$s^2$
$K$	0.005 $N m^2/A^2$
$R$	5$\Omega$
$L$	0.01$H$

请：

推导磁悬浮系统的状态空间模型：（提示：以钢球位置 $X$、速度 $\dot{X}$ 和电流 $I$ 为状态变量）
针对上述磁悬浮系统，设计模糊控制器使钢球位置稳定在期望位置 $X_d = 0.05m$。 假设初始钢球位置为 $X(0) = 0.03m$，初始速度和初始电流均为 0，仿真实现系统的模糊控制，绘制钢球位置随时间变化曲线、控制电压随时间变化曲线，并分析仿真结果。（输入输出的论域范围自行选择，可尝试位置误差范围 [-0.04,0.04]m，位置误差变化率范围 [-0.5,0.5]m/s，控制电压的范围 [-10,10]V）
若改变钢球质量为 0.1kg，其他参数不变，重新进行仿真并分析对系统控制性能的影响，讨论如何调整模糊控制器参数以适应钢球质量的变化。

完整的模糊推理系统介绍以及 matlab 中从零实现 ( 上篇 )_it can contain elements with only a partial degree-CSDN 博客

完整的模糊推理系统介绍以及 matlab 中从零实现 ( 下篇 )_tipper 模糊推理系统 -CSDN 博客

模糊控制方法在磁悬浮系统中的应用 - 道客巴巴

Generate Code for Fuzzy System Using Simulink Coder

神经网络控制 | Neural Network Control ¶

学习方法 ¶

监督学习
无监督学习
强化学习

训练方法 ¶

δ 学习规则

- 有师学习。 - 梯度下降法。

模拟退火算法

- 有师学习。 - 概率式学习。 - 基于模拟退火的统计优化方法 - 网络处于某一状态的概率主要取决于在此状态下的能量，能量越低，概率越大。同时，此概率还取决于温度参数T。

Hebb 学习规则

- 无师学习。 - 联想式学习方法。 - 两个神经元同时处于激发状态时，它们之间的连接强度将得到加强。

竞争式学习

- 无教师学习 - 神经网络中高层次的神经元对低层次神经元的输入模式进行竞争识别。

在建模辨识的应用 ¶

辨识是在输入和输出数据的基础上，从一组给定的模型中，确定一个与所测系统等价的模型。

控制和辨识的区别

控制的 loss 是瞬时的，而辨识的 loss 是一个积分

模型评价

模型精度 : 通常根据对学习样本和测试样本的输出误差来评价。
模型结构的复杂度 : 取决于实际应用。
模型的自适应性 : 对变化的环境，可方便地调整模型的结构和参数，且新的调整不会破坏或完全丢失原来学习已获得的结果。

考虑问题 ¶

模型的选择
- 存在精确性和复杂性的矛盾。例如，多层网络模型的节点数或隐层数的选择。
输入信号的选择
- 输入信号必须满足一定的条件：
  - 在辨识时间内，输入信号必须是持续激励的，即输入信号必须充分激励系统的所有模态。从频谱观点看，输入信号的频谱必须足以覆盖系统的频谱。
  - 所谓输入信号的最优设计问题，即设计输入信号使给定问题的辨识精度最高，常用的输入信号有白噪声或伪随机信号。

辨识的时候需要使用白噪声进行测试

误差准则的选择
- 误差准则是用来衡量模型接近实际系统的标准，它通常表示为一个误差的泛函。记作 $$ J(theta) = sum_{k=1}^{L} f[e(k)] $$
- 用得最多的是平方函数，即
  $$ f[e(k)] = e^2(k) $$

方法 ¶

系统辨识是一个优化问题。

一般辨识算法的基本原理，就是通过建立系统依赖于参数的模型，把辨识问题转化成对模型参数的估计问题。

针对线性系统或可线性化的系统，主要有三种方法

最小二乘法
梯度校正法
极大似然法

系统辨识只能利用输入输出数据，不能利用状态数据进行控制器的设计

模型结构 ¶

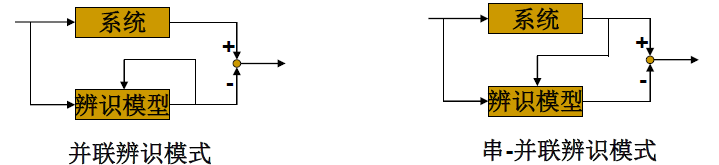
□ 并联模型：（动态反馈前向网络）

\[ \hat{y}_p(k+1) = f\left[\hat{y}_p(k), y_p(k-1), \cdots, \hat{y}_p(k-n+1); u(k), u(k-1), \cdots, u(k-m+1)\right] \]

不能使用 BP 算法，用于验证

□ 串 - 并联模型：（静态前向网络）

\[ \hat{y}_p(k+1) = f\left[y_p(k), y_p(k-1), \cdots, y_p(k-n+1); u(k), u(k-1), \cdots, u(k-m+1)\right] \]

可以使用 BP 算法，用于训练

神经控制的其他结构 ¶

建模、控制、优化都可以做

可以做系统辨识
可以做控制器设计
可以做优化器

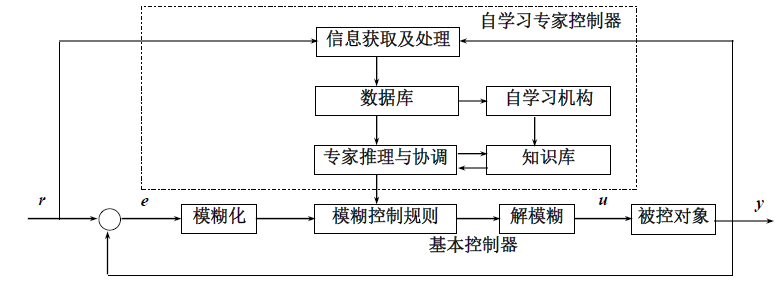
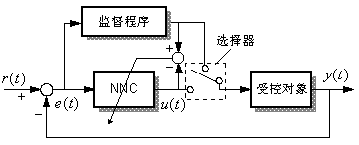
使用神经网络作为控制器，普通控制器作为监督器

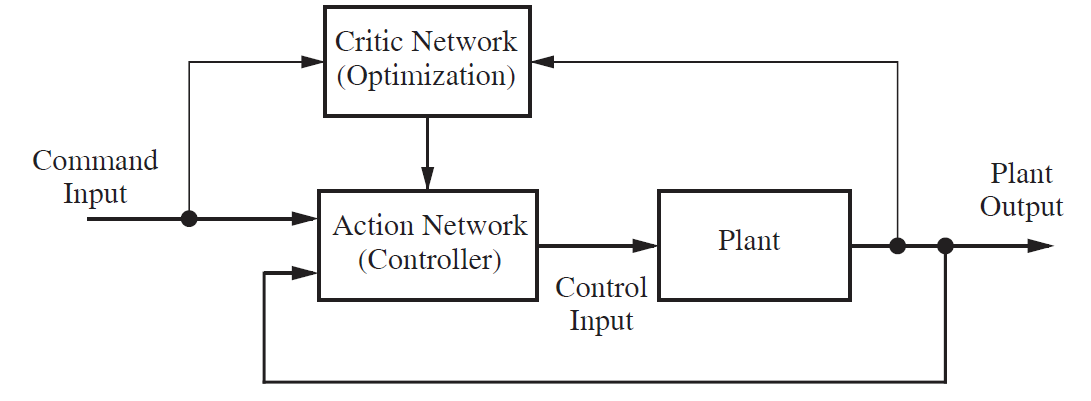
强化学习：critic

评价器也需要训练

逆模（u，y 反转）控制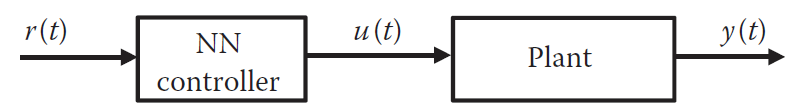问题： - 开环控制 - 逆模是非因果系统，不可以物理实现

HW04- 神经网络辨识 ¶

如图所示二自由度机械臂模型（平面俯视图），$q_1$ 和 $q_2$ 表示机械臂的两个关节角大小。

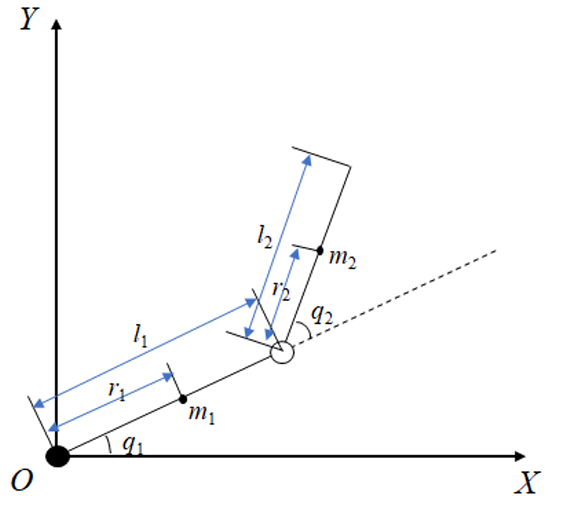
图中，$m_i, l_i, r_i (i=1,2)$ 分别为两连杆的质量、连杆长度和质心到相应关节的距离。

两个连杆的转动惯量分别为 $I_1$ 和 $I_2$。该机械臂动力学方程表示为：

\[ \begin{aligned} M(q)\ddot{q} + C(q, \dot{q})\dot{q} + G(q) = \tau \end{aligned} \]

$M(q)$ 为惯性矩阵，$C(q, \dot{q})$ 为科氏力和向心力的结合矩阵，$G(q)$ 为重力势能矩阵。

$\tau$ 为驱动力矩的向量。式 (1) 可写为如下方式：

\[ \begin{aligned} m_{11}\ddot{q}_1 + m_{12}\ddot{q}_2 + c_{11}\dot{q}_1 + c_{12}\dot{q}_2 + g_1 &= \tau_1 \\ m_{21}\ddot{q}_1 + m_{22}\ddot{q}_2 + c_{21}\dot{q}_1 + c_{22}\dot{q}_2 + g_2 &= \tau_2 \end{aligned} \]

$\tau_1$、$\tau_2$ 分别为关节 1 和关节 2 的驱动力矩。

定义以下参数：

\[ \begin{aligned} h_1 &= m_1r_1^2 + m_2l_2^2 + I_1 \\ h_2 &= m_2r_2^2 + I_2 \\ h_3 &= m_2l_1r_2 \tag{4} \\ h_4 &= m_1r_1 + m_2l_1 \\ h_5 &= m_2r_2 \end{aligned} \]

则式 (2) 和式 (3) 中的参数可按如下计算：

\[ \begin{aligned} m_{11} &= h_1 + h_2 + 2h_3 \cos(q_2) \\ m_{12} = m_{21} &= h_2 + h_3 \cos(q_2) \\ m_{22} &= h_2 \\ c_{11} &= -h_3 \sin(q_2) \dot{q}_2 \\ c_{12} &= -h_3 \sin(q_2) (\dot{q}_1 + \dot{q}_2) \\ c_{21} &= h_3 \sin(q_2) \dot{q}_1\\ c_{22} &= 0 \\ g_1 &= h_4 g \cos(q_1) + h_5 g \cos(q_1 + q_2) \\ g_2 &= h_5 g \cos(q_1 + q_2) \end{aligned} \]

式中，$g$ 为重力加速度 $9.8m/s^2$。

假定系统参数如下表所示

	数值
$h_1$	0.0308
$h_2$	0.0106
$h_3$	0.0095
$h_4$	0.2086
$h_5$	0.0631

请设计神经网络辨识方案，对该系统进行辨识（系统输入为 $\tau_1, \tau_2$，输出为 $q_1, q_2$）

参考步骤： 1. 利用已知系统得到辨识所需的输入输出数据； 2. 通过步骤1得到的数据来训练神经网络； 3. 对比原系统与神经网络辨识得到的系统是否一致。（给两个系统同样的输入，观察输出是否相同）（可以利用Matlab中的相关工具箱进行仿真）

在 Simulink 中设计 NARMA-L2 神经控制器

利用 NARMA 模型辨识非线性时变结构系统 - 豆丁网

让我们说人话

神经网络辨识，就是用神经网络来拟合一个系统，使得这个系统能够尽可能地逼近实际系统。

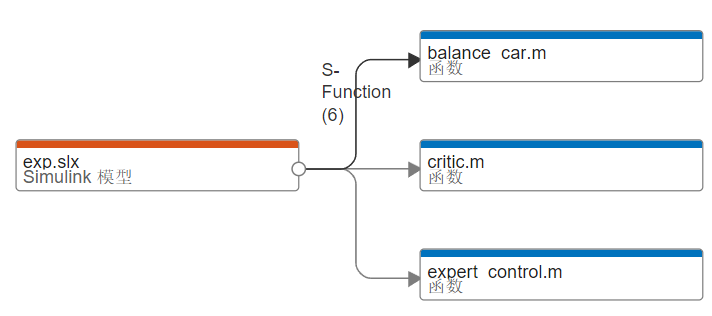
这个作业要做的就是

1. s-funtion 建立一个 model 2. 八仙过海获得其输入输出的数据 3. 使用神经网络工具箱进行训练（这里要注意使用串并联模型（把之前的输入输出都作为训练的data），真值作为label） 4. 使用训练好的神经网络进行仿真

BPPID¶

BP 神经网络 PID 控制器的设计与仿真 | RenAhahWiki

基于 BP 神经网络 PID 控制 +Simulink 仿真 - 腾讯云开发者社区 - 腾讯云

RBF¶

几种神经网络整定 PID 参数原理剖析及 simulink 案例仿真 _ 神经网络 pid-CSDN 博客

其他 ¶

遗传算法 ¶

遗传算法、遗传算法库函数 ga 和 gamultiobj、遗传算法工具箱 GOT 实例介绍 -CSDN 博客

基于遗传算法的 simulink/PID 参数整定 (s 函数）_ 基于遗传算法的 pid 控制参数优化 simulink-CSDN 博客

参数	大小
摆杆质量 \(m\)	0.5kg
小车质量 \(M\)	1kg
摆杆转动轴心到摆杆质心的长度 \(l\)	0.5m
摆杆与垂直向上方向的夹角 \(\theta\)	\([0, \pi]\) rad
重力加速度 \(g\)	9.8m/s²
施加在小车上的水平外力 \(F\)	\([-F_m, F_m]\) N
小车在水平方向的位移 \(x\)	不限制

参数	值
\(m\)	0.05kg
\(g\)	9.81m/\(s^2\)
\(K\)	0.005 \(N m^2/A^2\)
\(R\)	5\(\Omega\)
\(L\)	0.01\(H\)

	数值
\(h_1\)	0.0308
\(h_2\)	0.0106
\(h_3\)	0.0095
\(h_4\)	0.2086
\(h_5\)	0.0631

智能控制技术 ¶

递阶控制 | Hierarchical Control ¶

原理与结构 ¶

信息论 ¶

分层递阶 ¶

集散控制系统 ¶

HW01- 递阶控制 ¶

专家控制 | Expert Control ¶

概念 ¶

结构、类型与设计 ¶

专家 PID 控制 ¶

应用 ¶

HW02- 专家控制 ¶

模糊控制 | Fuzzy Control ¶

数学基础 ¶

原理与结构 ¶

merbership function¶

fuzzy rules¶

fuzzy operators¶

defuzzification¶

应用示例 ¶

作为控制器 ¶

作为决策系统 ¶

数据驱动 ¶

which parameters are we tuning?¶

how to tune them?¶

HW03- 模糊控制 ¶

神经网络控制 | Neural Network Control ¶

学习方法 ¶

训练方法 ¶

在建模辨识的应用 ¶

考虑问题 ¶

方法 ¶

模型结构 ¶

神经控制的其他结构 ¶

HW04- 神经网络辨识 ¶

BPPID¶

RBF¶

其他 ¶

遗传算法 ¶

粒子群算法 ¶

蚁群算法 ¶

评论