跳转至

经典控制方法

约 1805 个字 预计阅读时间 7 分钟

打通你任督二脉的自动控制领域知名博主 - 西门子工程师推荐 _ 哔哩哔哩 _bilibili

（1）镇定：状态 x(t) 渐近稳定，也就是当 t->∞时，x(t)->0

（2）跟踪：状态 x(t) 的跟踪误差 e(t)=z(t)-x(t) 或输出 y(t) 的跟踪误差 e(t)=z(t)-y(t) 镇定

（3）调节（Regulation）：说到英语，其实在机器学习里这个英语单词被翻译为 正则化，而正则化的目的是为了 “避免过拟合”，通常有 L1，L2 等方法，其实在最优化里面，调节通常用的是输入的 L2

跑步机上跑步 | 利用系统的输出量以参考数量的偏差进行控制，使系统的输出量与参考量之间的偏差尽可能小

田径赛跑 | 所谓最优控制就是寻找一个允许控制，使得被控系统在满足各种约束的条件下，使给定的性能指标达到最优

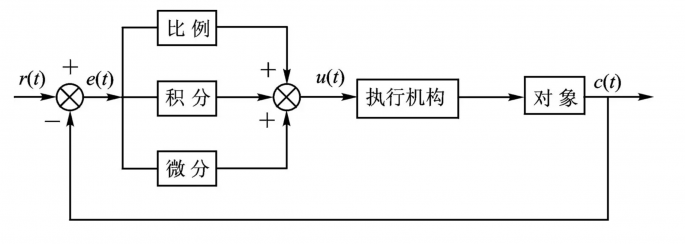
PID 控制

\[ u(t) = K_p e(t) + K_i \int_{0}^{t} e(\tau) d\tau + K_d \dot{e}(t) \]

K 是比例，I 是一阶积分（滞后），D 是一阶微分（超前）

可以测频率响应，进而使用补偿

其中： - \( u(t) \) 是控制量。 - \( e(t) \) 是误差，即设定值与实际值之间的差。 - \( K_p \) 是比例增益。 - \( K_i \) 是积分增益。 - \( K_d \) 是微分增益。 - \( \Delta e(t) \) 是误差的变化量。 - \( \Delta t \) 是时间间隔。

tuning

先是比例后积分，最后再把微分加， 曲线振荡很频繁，比例度盘要放大， 曲线漂浮绕大湾，比例度盘往小扳， 曲线偏离回复慢，积分时间往下降， 曲线波动周期长，积分时间再加长， 曲线振荡频率快，先把微分降下来， 动差大来波动慢，微分时间应加长， 理想曲线两个波，前高后低4比1， 一看二调多分析，调节质量不会低 。

先调整 P，再调整 D，最后看着调整 I

先只使用比例控制，增大 P 系数至系统震荡之后加入微分控制 D 以增大阻尼，抑制震荡，之后再结合系统对响应和静差等具体要求来调节比例 P 和积分 I 系数。

粗调 KP

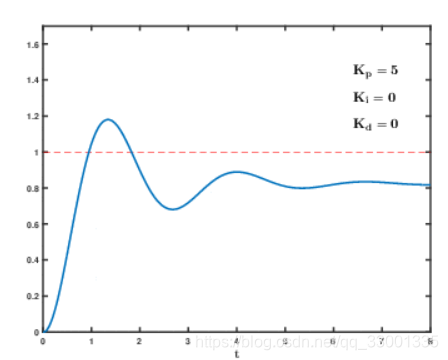
  1. 先将积分、微分系数置零，这样系统就是纯比例控制。接着逐渐增大比例系数 P，直至系统出现振荡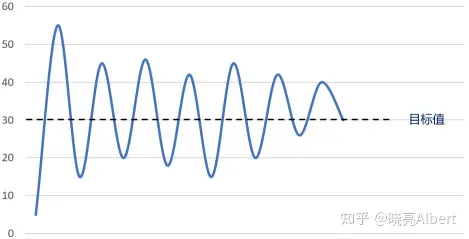； 当然，看到上面这个现象，一定要先确认一下系统硬件是否出现问题，比如电机堵转，电压不稳等，先排除硬件问题。

常见现象

  • 水温的保持中表现为温度不断上下浮动，且浮动的频率一定，最大值与最小值相差较小，
  • 在平衡车的调节中会导致平衡车一点点偏角就导致舵机打角程度十分巨大，跑起来就是左右左右不断晃动，但又勉强能跑。
  1. 我们可以看到上面比例系数过大，导致系统震荡，超调量很大。接着再逐渐减小比例系数，直至系统振荡消失。

调整 Kd

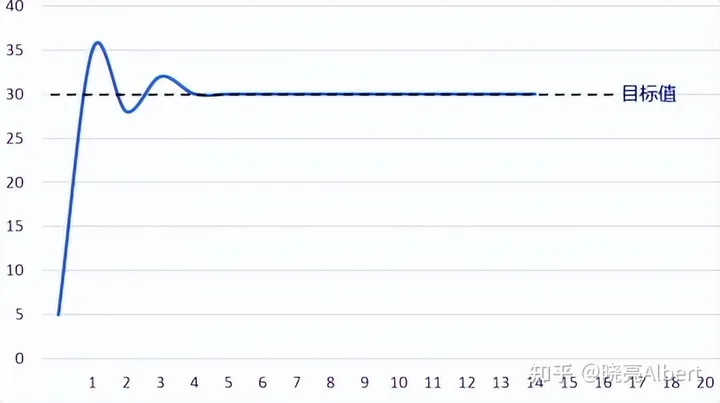
  1. 为了抑制这个小幅度超调，我们逐步增加微分比例系数 D, 直至超调量基本消失，如果此时效果较较佳，就不用考虑引入积分环节。

如上图我们可以看到引入微分环节之后，上升时间很短，超调量没有了，但是出现了静态误差。

现象

当 KP 调好，KI 为零，KD 调节过大时，水温会在达到目标值后猛地上升一下，然后回降一些，平衡车则会在你倾斜车身后猛地打死舵机，然后回过来一点

当你 KD 调好，那是什么情况？那就厉害了，水温可以保持一定温度挺久，平衡车可以跑得动了

调整 Ki

  1. 因为有了静态误差，我们就需要逐渐增大积分系数 I，并同时观察曲线的变化，如果消除静差的时间过长，则可以再适当增大积分系数，注意兼顾系统的最大超调量。

  2. 如果引入积分项之后系统的又出现微幅度超调，还是要继续增大点微分项来抑制，直至出现较好效果。

  3. 在工程实践中，不同的控制系统对控制效果要求不一样，比如平衡车对系统响应速度要求高，控制门窗的开合对快速性不高，但是对稳定性和准确性要求很高。所以我们要根据被控系统要求来调节参数，并不是所有系统都追求所有指标高。

PID 控制参数整定 ( 调参 ) 太高深莫测？一篇文章掌握通用调参思路 - 知乎

可视化

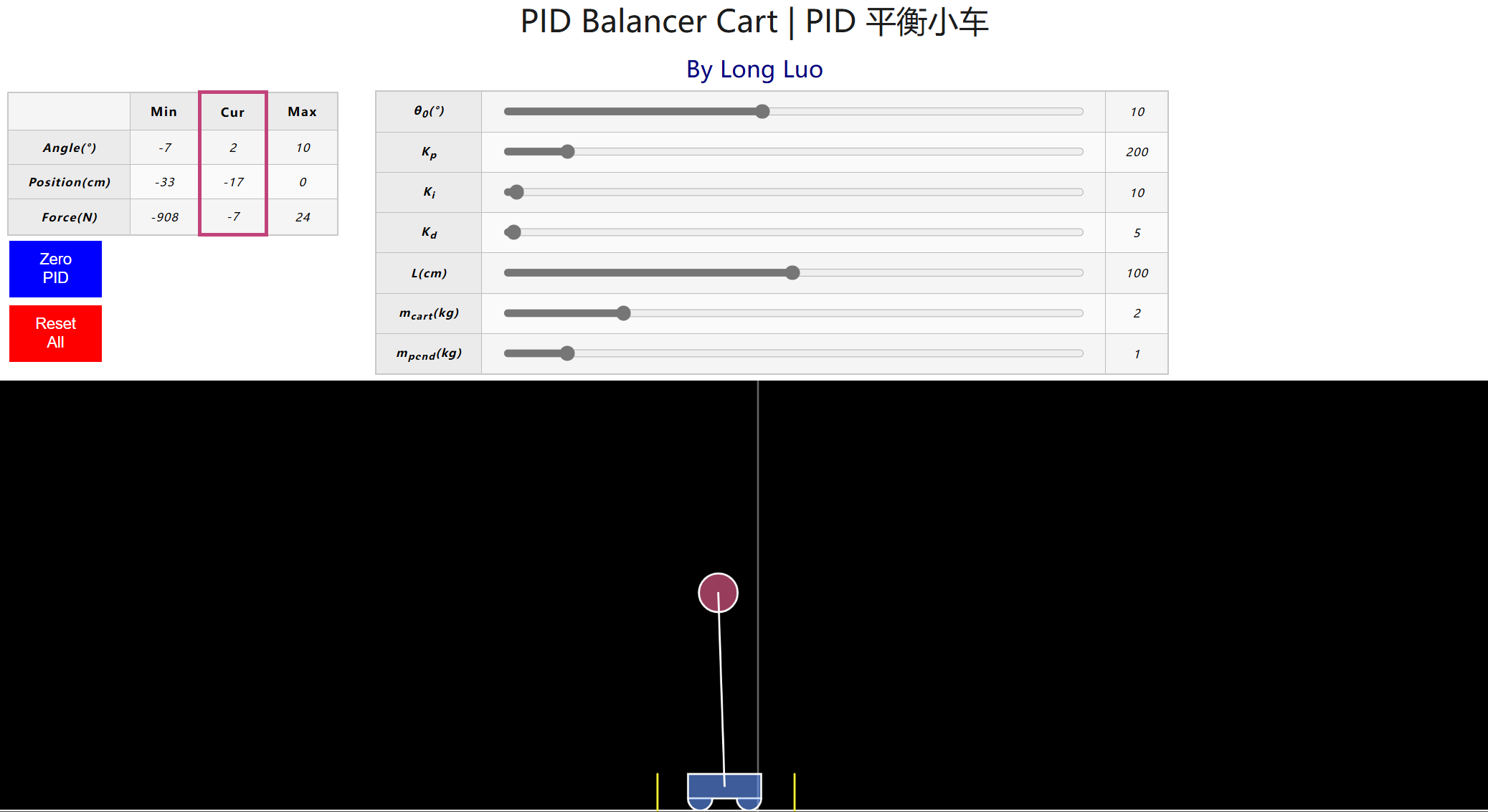
智能控制系统的灵魂：深入研究 PID 控制器的算法逻辑 | Long Luo's Life Notes

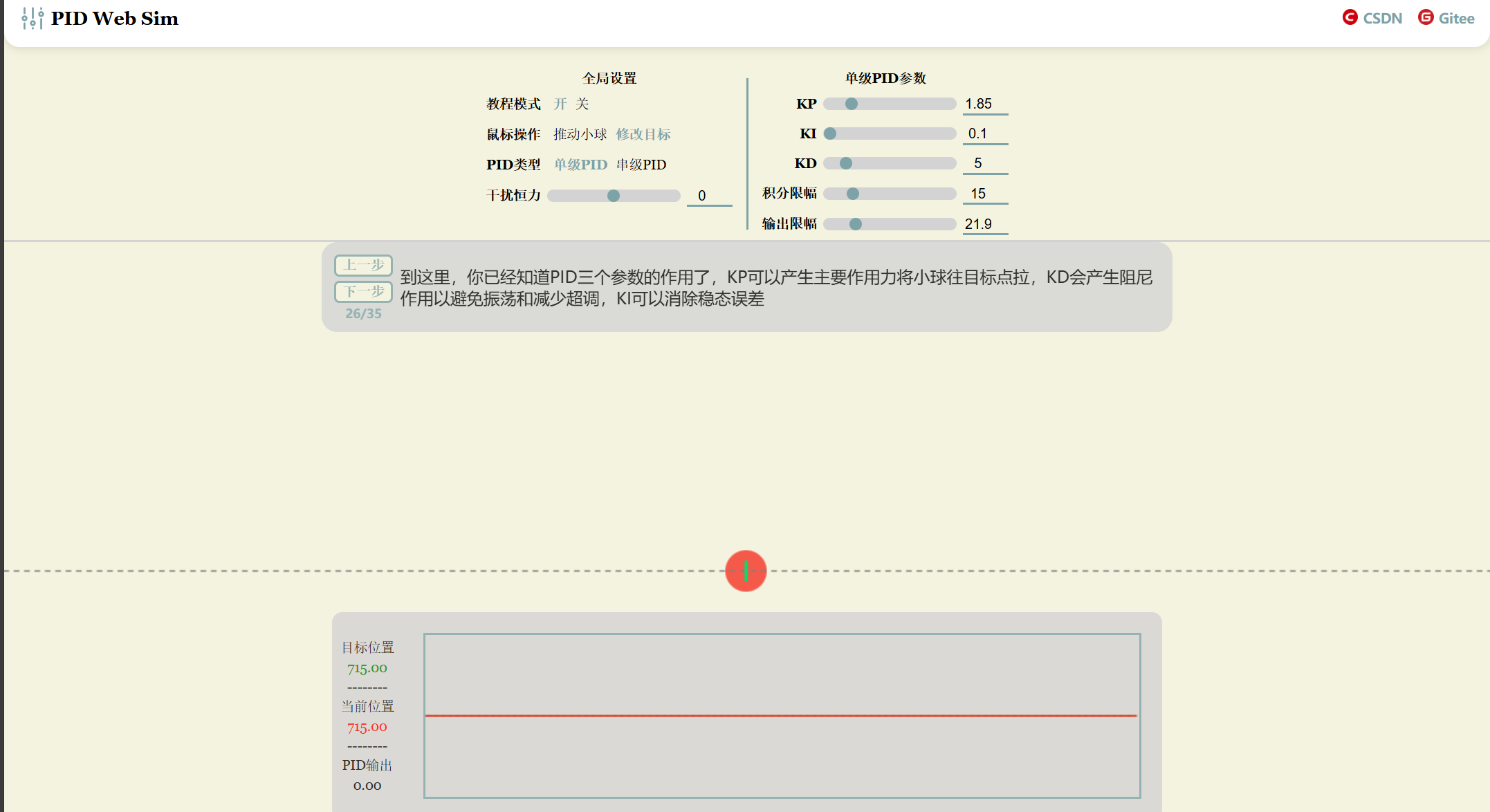
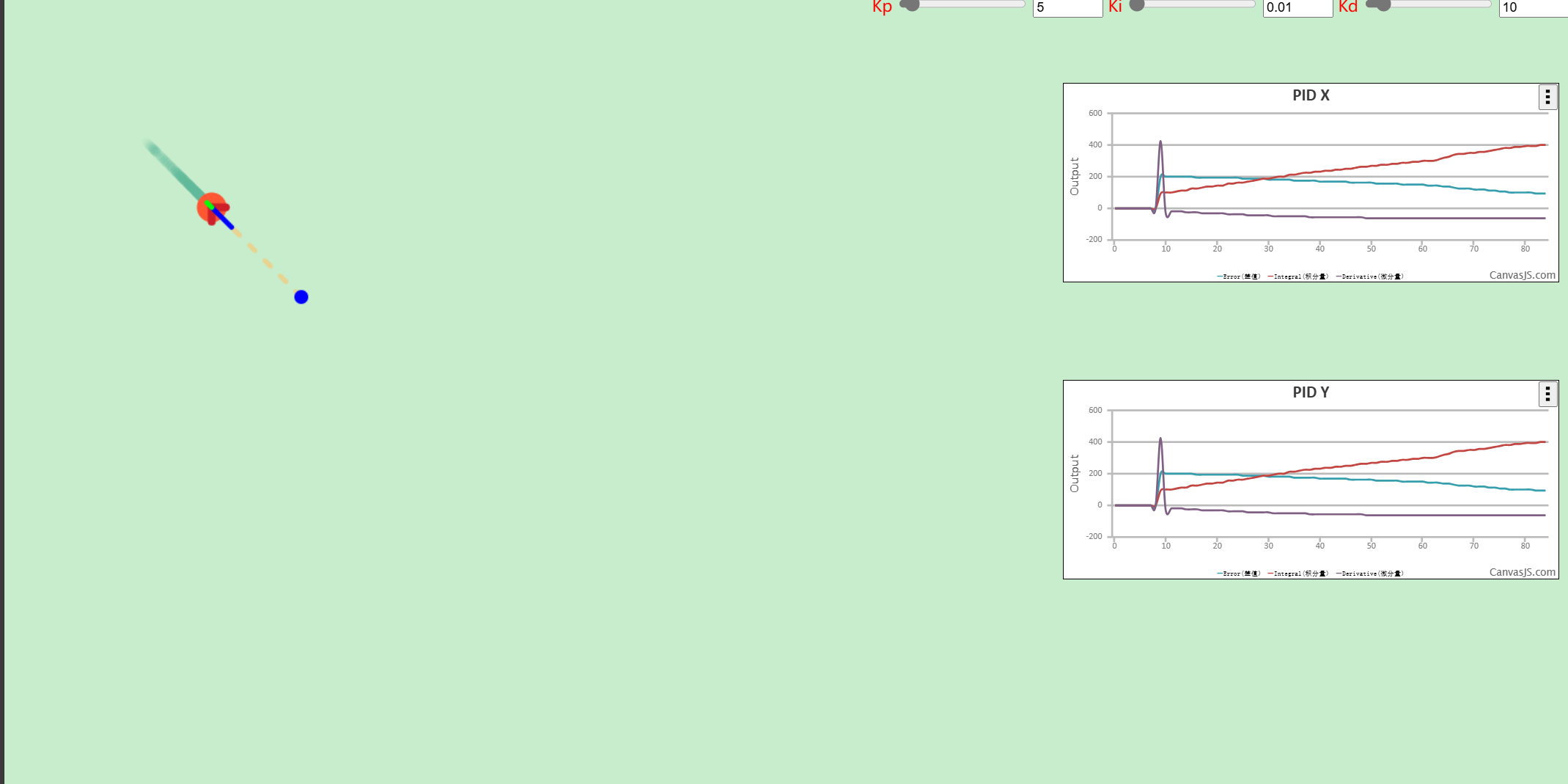
使用教程讲述了单级 PID 和串级 PID 的基本实现。可以动态调节参数对小球进行控制 PID Simulator

PID 小球

PID Balancer | PID 平衡车

LQR 控制

更加看重收敛速度，在 Q 上面做文章。更加看重输入的值的话，就在 R 上面做文章

对于一个线性时不变系统，其状态方程可以表示为：

\[\dot{x} = Ax + Bu\]

LQR 的 cost function 可以表示为：

\[ J = \int_{t_0}^{t_f} \left( \mathbf{x}^T \mathbf{Q} \mathbf{x} + \mathbf{u}^T \mathbf{R} \mathbf{u} \right) dt \]

cost function

Q: 表达的是因为系统变化而造成的能量损耗

权重矩阵 \(Q\) 和 \(R\) 用于调整系统状态和控制输入在 cost function 中的相对重要性。

LQR 的目标是找到一个控制策略 \(u^*(x)\)，使得对于任意的初始状态 \(x_0\)，cost function \(J\) 都达到最小值。这可以通过求解一个优化问题来实现，其中控制输入 \(u\) 是优化变量，cost function \(J\) 是优化目标。

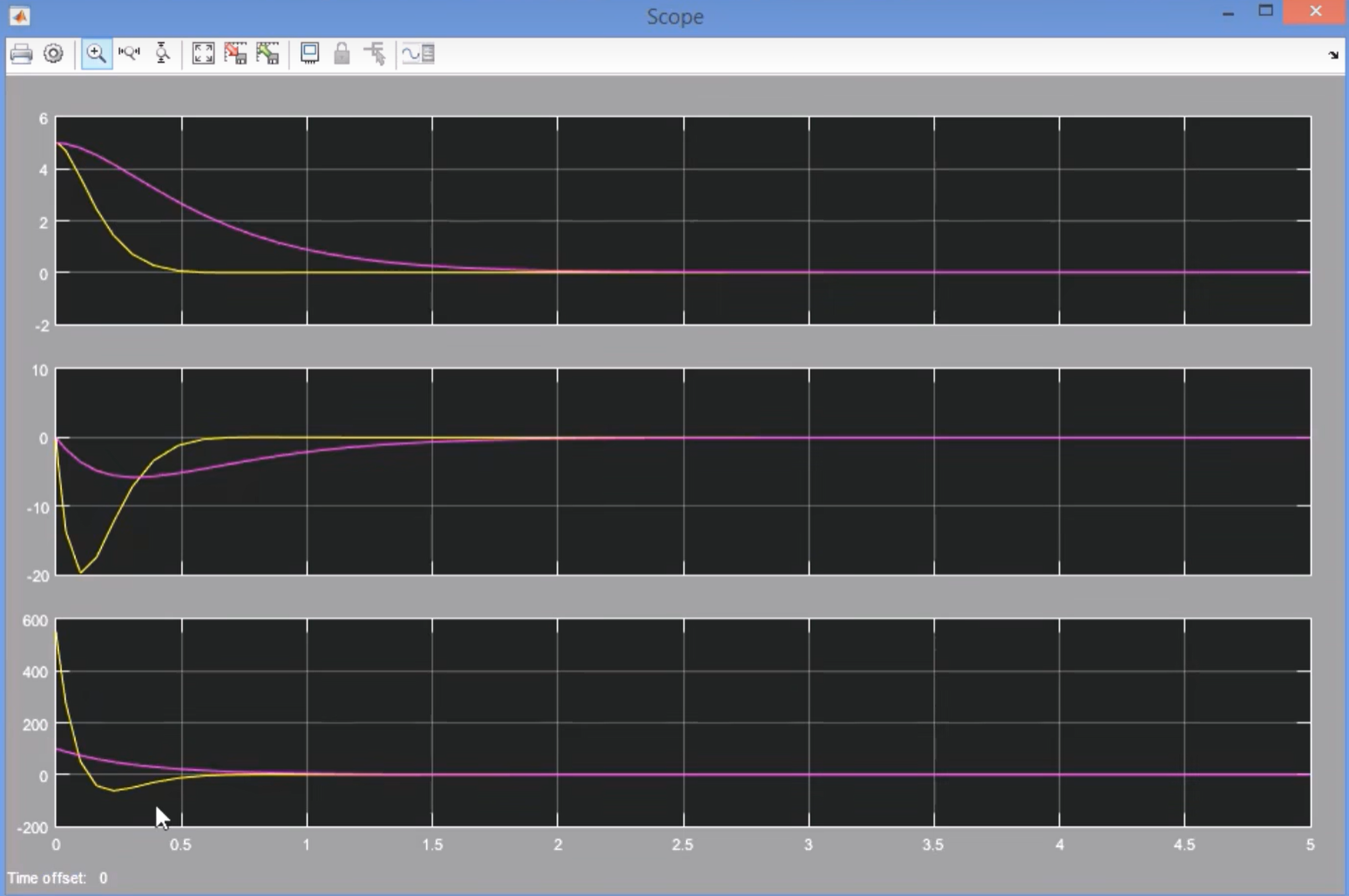
如图，黄线是选用较大的 Q，可以看到快速收敛但是输入值较大；紫线是选用较大的 R，可以看到输入值较小，但是收敛速度较慢。

MPC 控制

fix horizon，N 是固定的

解了十个指令，只执行 1 个指令

别名： - 开环最优反馈 - 反应式规划 - 滚动优化控制

优势 - 考虑未来时域 - 考虑误差 - 减少问题规模

可以解很多问题，不仅是轨迹跟踪

不想指定最后 terminal cost

而不加的话，有可能不动

所以加一个正则项，让他动起来

预测时间和计算量是一个 balance

线性有约束或者非线性有约束需要一些人为的约束

无约束 MPC = 线性反馈控制

一个线性无约束的 MPC 解析最优解是一个关于初值的最优反馈

CMPCC

有障碍物的 RC 小车控制

飞机竞速

桨叶失效

else

阻抗 / 导纳控制最强解析 - 知乎

评论