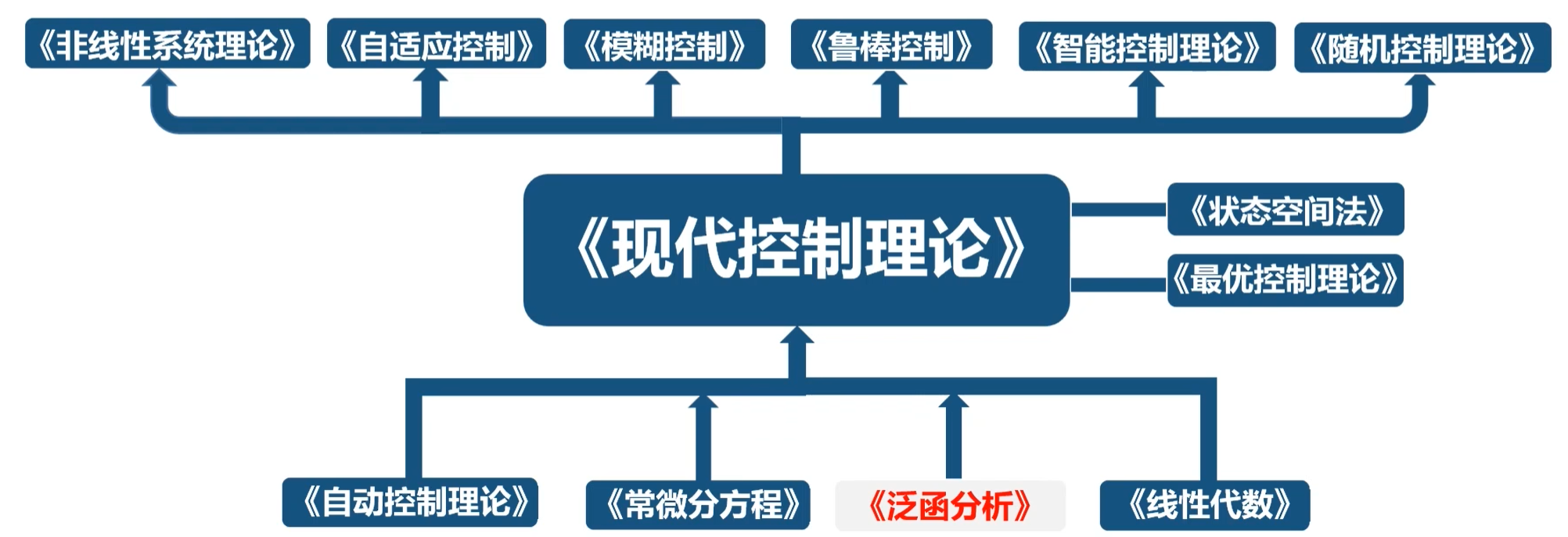
现代控制理论 ¶
约 6021 个字 13 行代码 预计阅读时间 24 分钟
以此笔记致敬 DR_CAN,感谢他的无私奉献
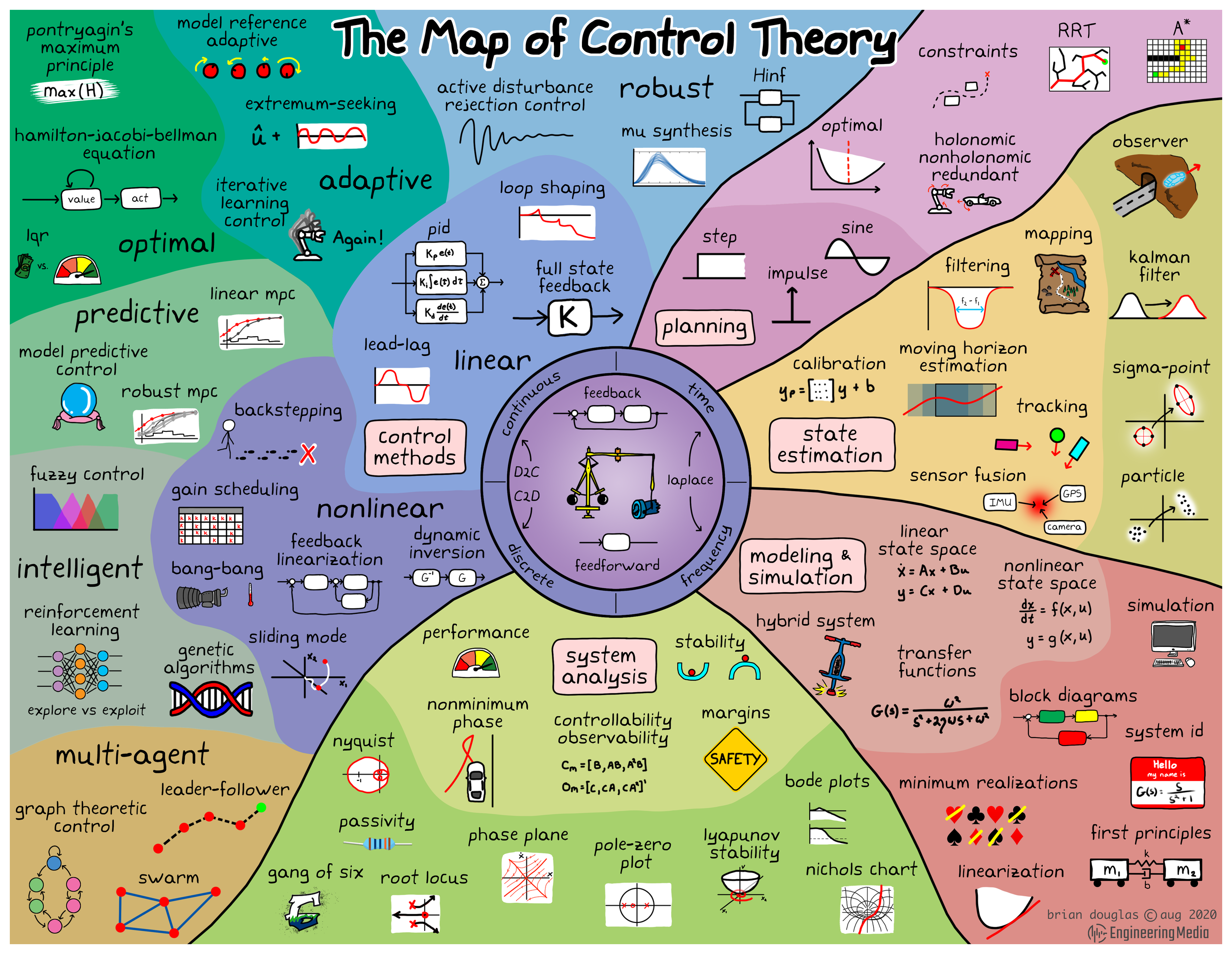
资源汇总
- DR_CAN 现代控制理论系列课程 + 王崇卫笔记
- 课本阅读
- 作业题目
- 课件
- 历年题目
通过百度网盘分享的文件:现代控制理论
链接:https://pan.baidu.com/s/1YUCIKVOh5ZZdMgX8pZrZ4A?pwd=92t1
提取码:92t1
./
│ 现代控制理论.svg
│ 现代控制理论.xmind
│
├─01-作业
│ 01周作业参考答案.pdf
│ 02周作业参考答案.pdf
│ 03周作业参考答案.pdf
│ 05周作业-答案.pdf
│ 06周作业参考答案.pdf
│ 07周作业参考答案(1).pdf
│ 08周作业参考答案.pdf
│
├─02-实验
│ ├─Matlab
│ │ experiment1_1.m
│ │ experiment1_2.m
│ │ experiment1_3.m
│ │ matlab 实验参考指导书_1.pdf
│ │ matlab 实验参考指导书_2.pdf
│ │ Matlab实验1.pdf
│ │ matlab实验.docx
│ │ Matlab实验2.pdf
│ │ matlab实验.docx
│ │ Untitled.m
│ │ Untitled2.m
│ │ Untitled3.m
│ │ 实验一代码.rar
│ │ 实验二代码.rar
│ │
│ └─线下
│ 二阶系统瞬态响应分析.docx
│ 实验1 控制系统典型环节的模拟(24版).pdf
│ 实验2 二阶系统的瞬态响应分析(24版).pdf
│ 实验3 线性系统的频率特性的测试(24版).pdf
│ 控制系统典型环节的模拟.docx
│ 线性系统的频率特性测试.docx
│
├─03-PPT1
│ Feedback Control of Dynamic Sys - Gene F. Franklin.pdf
│ Linear Control System Analysis and Design.pdf
│ modern control systems 13th Richard C.Dorf.pdf
│ 第7章-1-采样过程.pdf
│ 第7章-2-Z变换.pdf
│ 第7章-3-差分方程&脉冲传递函数.pdf
│ 第7章-4-状态空间&关系.pdf
│ 第7章-5-稳定性与性能.pdf
│ 第7章-6-离散系统设计.pdf
│ 第8章-1-状态空间简介.pdf
│ 第8章-2-能控性与能观性.pdf
│ 第8章-3-线性变换与标准型.pdf
│ 第8章-4-状态反馈.pdf
│ 第8章-5-状态反馈-2.pdf
│ 第8章-6-状态观测器.pdf
│ 第9章-1-非线性控制系统.pdf
│ 第9章-2-Lyapunov稳定性.pdf
│
├─04-PPT2
│ CHAP7-1-20240911(1).pdf
│ CHAP7-2-20240914.pdf
│ CHAP7-3-20240918.pdf
│ CHAP7-4-20240920.pdf
│ CHAP7-5-20240925.pdf
│ CHAP7-6-20240927.pdf
│ CHAP7-7-20240929.pdf
│ 课件8-1.pdf
│ 课件8-2-1.pdf
│ 课件8-2-2.pdf
│ 课件8-3.pdf
│ 课件8-4.pdf
│ 课件8-5.pdf
│ 课件8-6.pdf
│
└─05-A4
A4_Healor.pdf
A4_PhilFan.pdf
A4_追风Holy.pdf
现代控制理论_A4.pdf
课程感想 ¶
现代控制理论算是大三秋冬还算学到东西的一门主修课了,个人大部分内容都是自学的,因为上课容易走神,而且每次早八都有点困困的
现控上课时间只有半个学期,也就意味着课程节奏是很快的。最后一章甚至都是在考试前一天才讲完
从考试来看,笔者和朋友们都感觉题目计算量很大(尤其是涉及到矩阵的计算、z 变换的化简等题目
本门课程的实验可以用依托答辩来形容,实验分为三次线下实验箱实验与两次线上 matlab 实验。线下可以说与现代控制这学期所学的内容关联不大,甚至把它放在模电实验中我觉得也没有什么违和感
甚至直接去签完到回去写实验报告都不一定比别人低
总论 ¶
以下内容均为笔者个人理解,如有错误,先滑跪
纯为了搭一个大致的框架,肯定会有很多表述不太严谨的地方
现代控制理论是经典控制理论的延续。更关注于离散系统和多输入系统。
可以先听一下这个串讲,对整体有一个了解 现代控制理论串讲 - DR_CAN
首先要理解状态空间模型,求传递函数
其中,A 是系统矩阵,B 是输入矩阵,C 是输出矩阵,D 是直接传递矩阵;u 是输入,y 是输出,x 是状态
因为计算机只能处理离散数据,所以需要将连续系统离散化,这里使用的工具是 \(\mathscr{z}\) 变换
Open Loop:其次要理解系统状态矩阵 \(\mathbf{A}\)
- 矩阵 \(\mathbf{A}\) 特征值的实部决定了系统的稳定性,与 \(|\lambda I - A|\) 判定方法是一样的
Close Loop:
了解了稳定性之后,我们就可以通过设计闭环特征矩阵 \(\mathbf{A_{cl}} = \mathbf{A} - \mathbf{B}\mathbf{K}\) 来把极点配置到我们想要的位置: - 先列出期望系统的特征多项式,再列出\(\mathbf{A_{cl}}\)的特征多项式,系数对应,求解合适的K参数 - 可以使用LQR控制器来配置极点达到不同的目标效果
能控性和能观性
- 能控性:是否可以从一个点控制到另一个点(不是路径控制
) ,如果能控,就可以使用上边的方法任意配置极点。 - 能观性:并不是所有的状态都可以被观测到,所以需要设计观测器来估计系统的状态,即能否利用输入输出量把状态计算出来,就不用使用传感器了。
- 可以根据 observer 观测的结果来设计控制器进而控制系统
这里需要掌握的知识点还有:能控性的判断(\(Co\) 矩阵
最常用公式 ¶
| 采样函数 \(y(kT)\) | Z 变换 \(Y(z)\) | 拉氏变换 \(Y(s)\) | 时域原函数 |
|---|---|---|---|
| \(\delta(kT)\) | 1 | 1 | \(\delta(t)\) |
| \(\delta[(k-n)T]\) | \(z^{-n}\) | \(e^{-nTs}\) | \(\delta(t-nT)\) |
| 1 | \(\frac{z}{z-1}\) | \(\frac{1}{s}\) | \(u(t)\) |
| \(kT\) | \(\frac{Tz}{(z-1)^2}\) | \(\frac{1}{s^2}\) | \(t\) |
| \(\frac{1}{2!}(kT)^2\) | \(\frac{T^2z(z+1)}{2(z-1)^3}\) | \(\frac{1}{s^3}\) | \(\frac{1}{2}t^2\) |
| \(e^{-akT}\) | \(\frac{z}{z - e^{-aT}}\) | \(\frac{1}{s + a}\) | \(e^{-at}\) |
| \(kTe^{-akT}\) | \(\frac{Tze^{-aT}}{(z - e^{-aT})^2}\) | \(\frac{1}{(s + a)^2}\) | \(t e^{-at}\) |
| \(1 - e^{-akT}\) | \(\frac{z(1 - e^{-aT})}{(z - 1)(z - e^{-aT})}\) | \(\frac{a}{s(s + a)}\) | \(1-e^{-at}\) |
离散系统描述 ¶
零输入分量: \(x(t) = 0,f(0^+) = f(0^-)\) 零状态分量: \(f^{n}(0^-) = 0\)
采样 ¶
就像减肥过程称体重,比如说你每十分钟就测一次体重:这就会产生两个问题 - 体重并不是一个快速响应的系统,需要时间体现变化,会采集到大量重复信息 - 读取这个体重后开始参考制定计划,计划还没有制定出来,就需要进行下一次测量了
离散系统例子
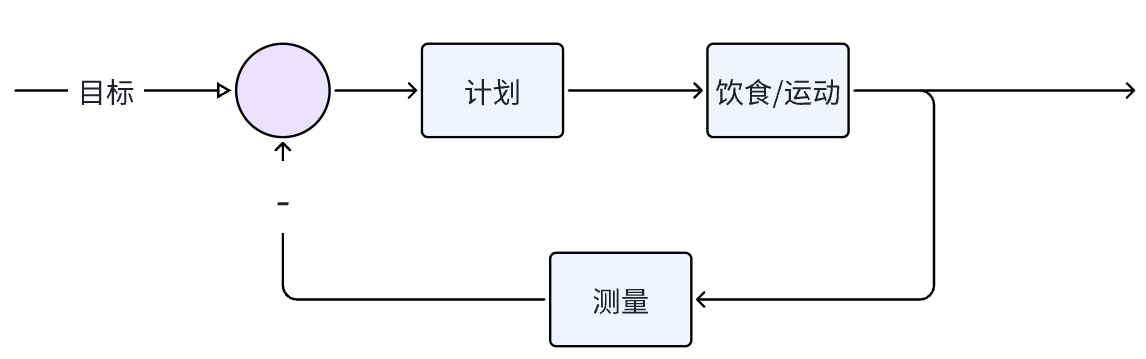 控制体重的例子
控制体重的例子
如果测体重测得太频繁,那么根本来不及计划
z 变换 ¶
- 留数法
- 超前滞后定理
- 初值定理、终值定理
- 差分方程求解
要注意微分方程的离散化 x(t) 变成 x(nT) 才可以
脉冲传递函数 ¶
脉冲传递函数:\(G(z) = \frac{Y(z)}{U(z)}\) ,零初始条件下,系统的输出采样函数的 z 变换和输入采样函数的 z 变换的比值
零阶保持器: \(G_h(s) = \frac{1-e^{-Ts}}{s},G(z) = 1\)
trick: 先把 \((1-z^{-1})\) 提出来
推导法
闭环脉冲传递函数 \(\Phi(z) = \frac{C(z)}{R(z)}\), 如果前向通道第一个传递函数之前没有采样开关,就没有办法求解,只能求 \(C(z)\)
- \(\mathcal{Z}[A(s)B(z)] = A(z)\cdot B(z)\)
- \(\mathcal{Z}[A(s)B(s)] = AB(z) \ne A(z)B(z)\)
Mason 增益公式法
一个讲的很好的视频:离散系统关于脉冲传递函数求法 _ 哔哩哔哩 _bilibili 相连的写一起,有开关的分开写
回路只要有连在一起,就不能分开算 z 变换
模拟化设计 ¶
s = tf('s');
z = tf('z',0.015);
D = 20*(s+4)/(s+10);
Back = (21.2-20*z^(-1))/(1.15-z^(-1)); %后向差分
zeroholder = c2d(D,0.015); %0阶保持器
Forward = 20*(z-0.94)/(z-0.85); %前向差分
Tustin = (19.16-18.05*z^(-1))/(1-0.86*z^(-1));%双线性变换
k = 8*(1-exp(-0.15))/(1-exp(-0.06));
P_Z = k*(1-z^(-1)*exp(-0.06))/(1-z^(-1)*exp(-0.15));%零极点配置法
step(Back,zeroholder,'--',Forward,'-',Tustin,'r--',P_Z,'y-',D,'g-');
legend;
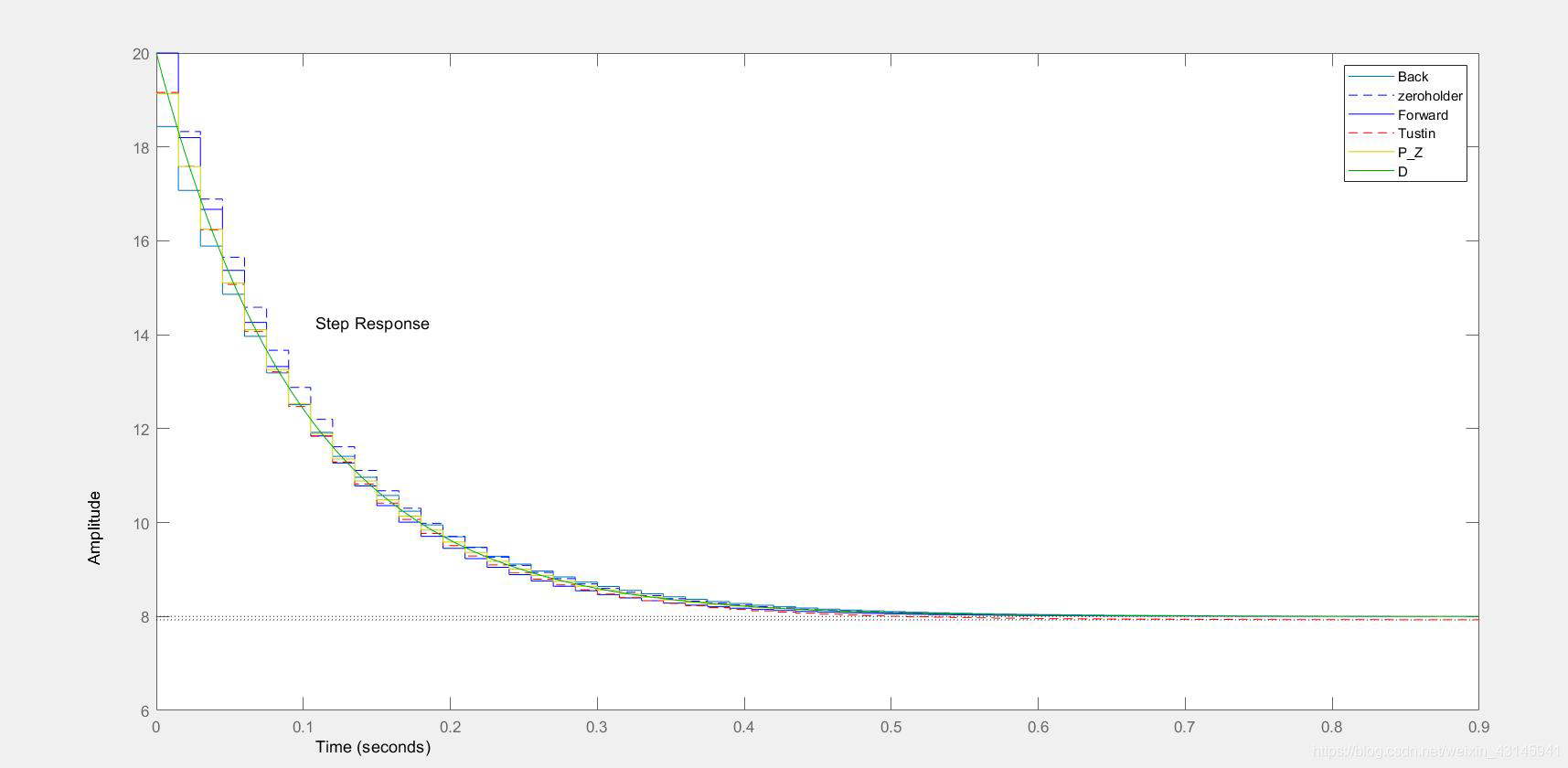
z 域根轨迹设计
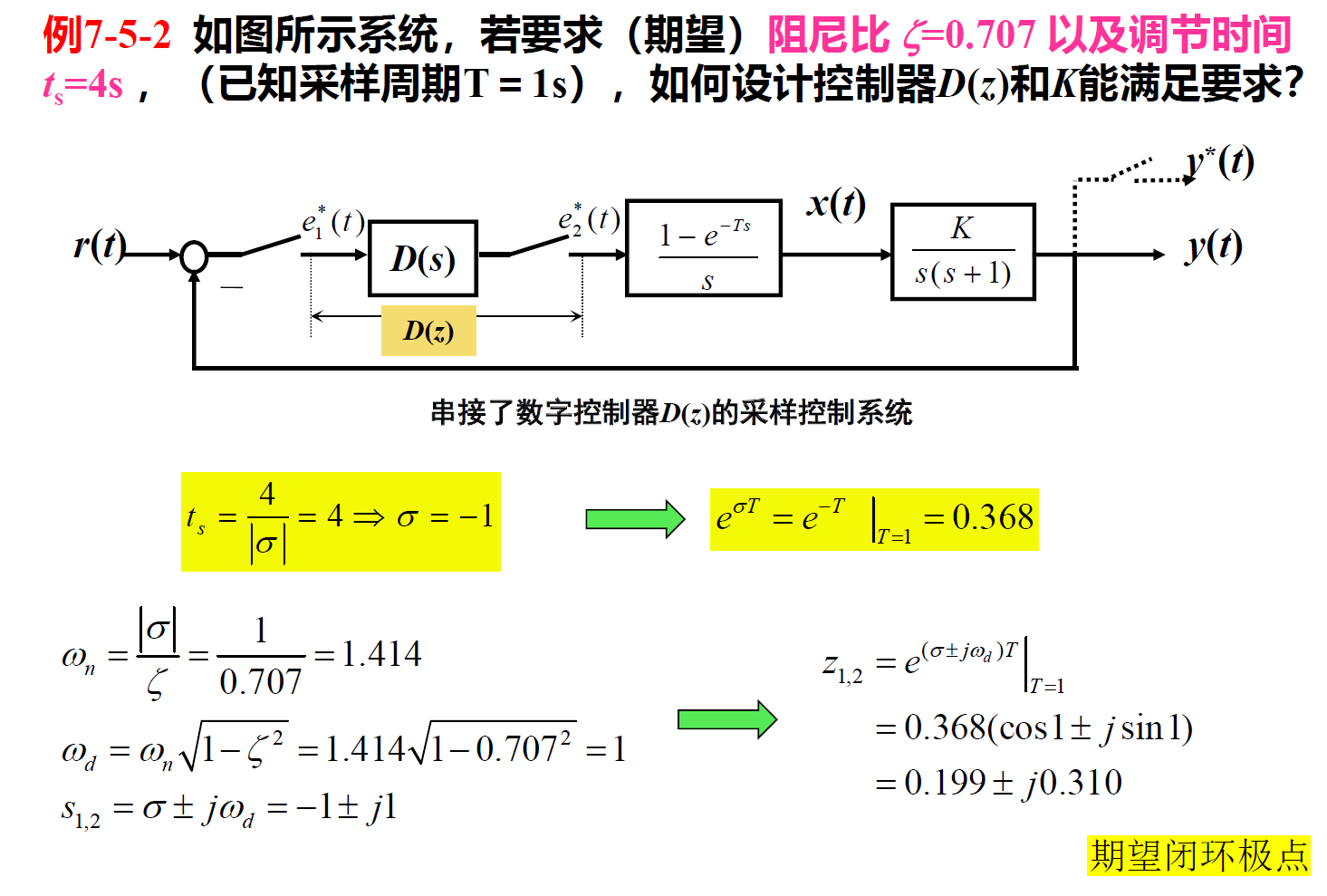

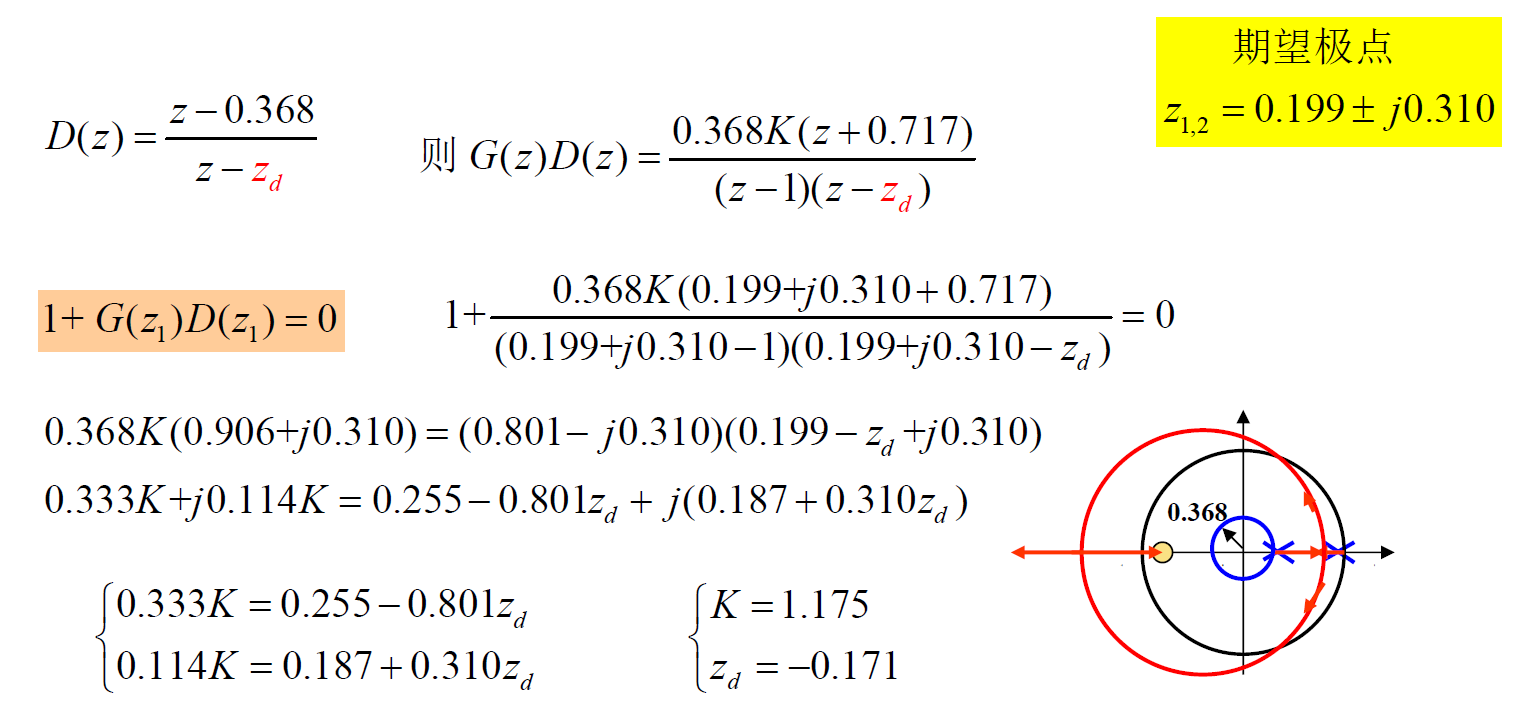

数字化设计 ¶
z 域解析设计的方法主要有最少拍系统设计、无波纹最少拍系统设计、最小均方差系统设计等
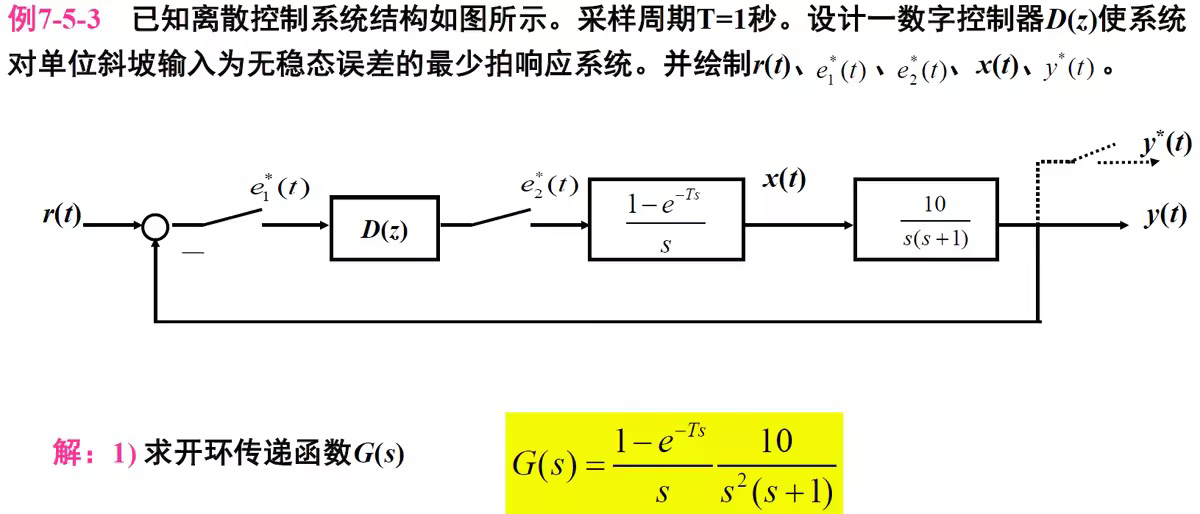
如下图的系统,我们只能设计 D(z) 部分,而 \(H(s)\) 与 \(G_c(s)\) 是给定的。

z 域解析设计的方法关键是根据性能指标的需要选择合适的闭环脉冲传递函数 \(\Phi(z)\) 或闭环误差脉冲传递函数 \(\Phi_e(z)\)。
求无稳态误差最小拍系统 ¶
- 求解输入:\(A(z^{-1})\) 为不含 \((1 - z^{-1})\) 的 \(z^{-1}\) 多项式
-
求解 \(\Phi_e(z)\) \(\Phi_e(z) = (1 - z^{-1})^mF(z)\) ,取 \(F(z) = 1\)
-
按照公式求解 \(D(z)\)
| 典型输入 | 闭环脉冲传递函数 | 数字控制器 D(z) | 最少拍 (T) |
|---|---|---|---|
| \(1(t)\) | \(\frac{1}{1 - z^{-1}}\) | \(\frac{z^{-1}}{G(z)(1 - z^{-1})}\) | 1T |
| \(t\) | \(\frac{Tz^{-1}}{(1 - z^{-1})^2}\) | \(\frac{z^{-1}(2 - z^{-1})}{G(z)(1 - z^{-1})^2}\) | 2T |
| \(t^2\) | \(\frac{T^2z^{-1}(1 + z^{-1})}{(1 - z^{-1})^3}\) | \(\frac{3z^{-1} - 3z^{-2} + z^{-3}}{G(z)(1 - z^{-1})^3}\) | 3T |
例子


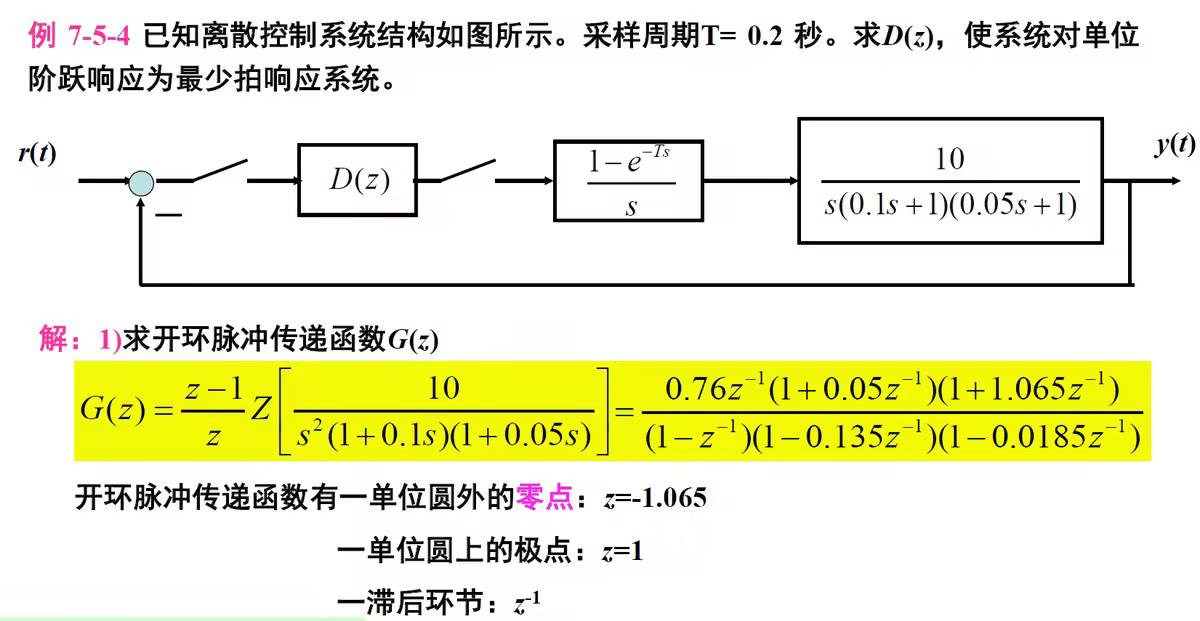

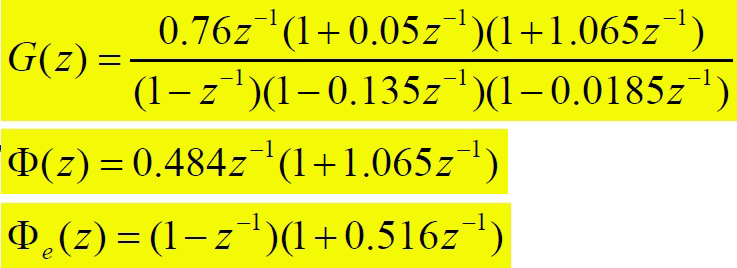

状态空间求解 ¶
状态空间是一组将输入、输出、状态联系在一起的一阶微分方程。
A 的特征值就是 \(G(s)\) 的极点
状态空间与极点的关系
- 特征向量 : \(Av = \lambda v\) 在一条直线上
- 对角化的方法
- \(P^{-1}A P = \Lambda\)
- \(\dot{X} = AX,X = PY,\dot{Y} = \Lambda Y\)
递推法求解
\(\mathscr{z}\) 变换
对上式 \(\mathscr{z}\) 变换
求得
连续方程求解
解可以写成
其中第一项状态转移矩阵 (State Transition Matrix) \(\Phi(t-t_0) = e^{\mathbf{A}(t-t_0)}\) 描述了系统在没有输入的情况下,从初始状态开始的演化 . 第二项是一个卷积,描述输入与输出的关系
其中
计算转移矩阵 \(e^{AT}\)
- 泰勒 + 化简
- Laplace
- 矩阵 A 对角化
- Cayley-hamilton

推导
左右同乘以 \(e^{-At}\),移项得到:
对上式两边积分:
稳定性 ¶
对于 \((A,b,c,d)\),\(G(s) = c(sI-A)^{-1}b+d\) 的极点是能控能观子系统的极点,G(s) 稳定称为外稳定
\((A,b,c,d)\) 所有极点位于 S 左半开平面称为内稳定
phase portrait¶
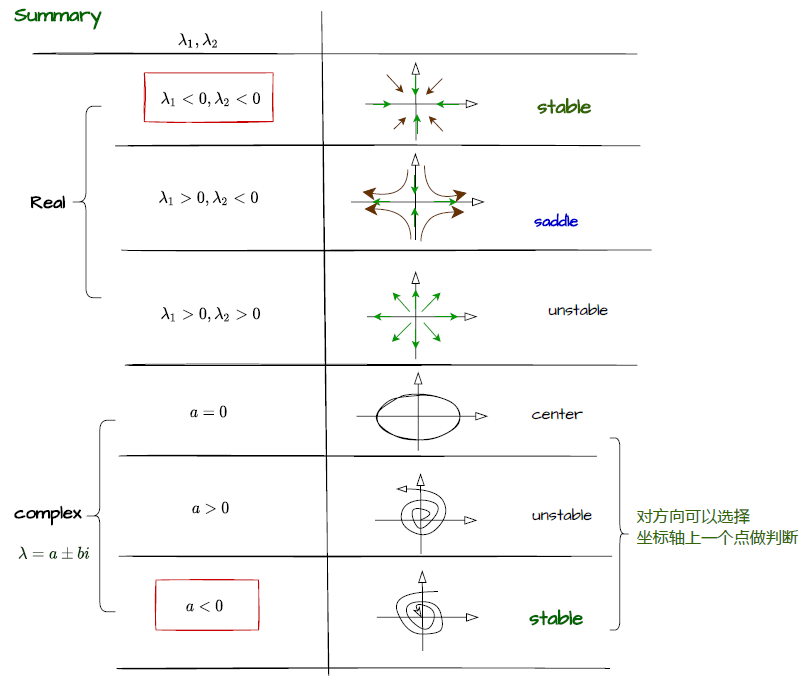
- sink: 槽 ; \(a<0\ and\ d<0\)
- source \(a>0 \ and \ d > 0\)
- saddle \(ad < 0\)
非常无敌的视频
绘制相平面图像 MathWorks-Teaching-Resources/Phase-Plane-and-Slope-Field: Apps for qualitative ODE analysis.
稳定条件 ¶
- 特征根具有负实部
- A 的特征值
- z 传递函数分布在单位圆内部
引入采样器会降低稳定性
trick
特征值之和等于矩阵的迹
特征值之积等于矩阵的行列式
可以用来迅速判断不稳定的情况
| stability | \(\lambda = a+bi\) |
|---|---|
| lyapunov | \(a \le 0\) |
| 渐进 | \(a < 0\) |
| 不稳定 | \(a>0\) |
Lyapunov 稳定性定义 ¶
稳定性都是相对于某个稳定状态 \(x_e\) 而言
自治系统与非自治系统
考虑如下系统:
其中 \(x = [x_1, x_2, \ldots, x_n]^T \in \mathbb{R}^n\) 是系统状态,\(t > 0\) 是时间。
\(f(t, x)\) 中显含时间 \(t\) 的系统就是非自治系统(nonautonomous system
如果不显含时间 \(t\),即
称为自治系统(autonomous system
注 1:决定自治和非自治的是是否“显含时间 \(t\)”。注意这里的描述是“显含”而不是“不含”。事实上,\(x\) 本身就是时间的函数,即 \(x = x(t)\),也就是说系统 (1) 的完整描述是 \(\dot{x}(t) = f(t, x(t))\),系统 (2) 的完整描述是 \(\dot{x}(t) = f(x(t))\)。\(x(\cdot)\) 中包含的时间 \(t\) 对于系统来说不是显含的,而是隐含的,所以 \(x(\cdot)\) 中所包含的时间 \(t\) 与判断系统是否自治无关。
注 2:如果 \(f\) 是线性的,那么系统 (1) 就是线性非自治系统(线性时变系统
Lyapunov: the origin(equilibrium point at the origin) is stable(在于有界)
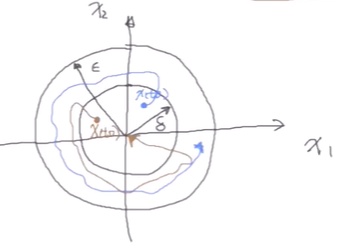
\(\forall t_0,\forall\epsilon>0, \exists \delta(t_0,\epsilon): ||x(t_0)||<\delta(t_0,\epsilon) \Rightarrow \forall t\ne t_0 ||x(t)||<\epsilon\)
出发点 \(x_0\) 有限制,轨迹线有限制
\(x(t_0)\) 是起始点,给定 \(\epsilon\) 和 \(\delta\) 不会出边界(蓝色线条)
asymptotically stable(在于随着时间趋于零)
\(\exists \delta(t_0)>0: ||x(t_0)||<\delta(t_0) \Rightarrow \lim_{t\rightarrow\infty}||x(t)|| = 0\)
最后会回到原点(棕色线条)
大范围渐进稳定:
必要条件:只有一个平衡状态;出发点 \(x_0\) 没有限制;对于线性系统,平衡状态渐近稳定则必然大范围渐进稳定
Lyapunov 第一方法——间接法 ¶
通过求解系统的微分方程式,然后根据解的性质来判断系统的稳定性
- 求解平衡状态
- 写出雅可比矩阵
- 求解 \(A|_{x_{e1}},A|_{x_{e2}}\) 的特征值
- 都为负,渐近稳定
- 存在正,不稳定
- 含有0,该法失效
Lyapunov 第二方法——直接法 ¶
若系统的某个平衡状态是渐近稳定的,则随着系统的运动,其存储的能量将随时间的增长而不断衰减,直至系统运动趋于平衡状态,而能量趋于极小值。
Lyapunov 创建了一个可以模拟系统能量的 “广义能量”函数 ,根据这个标量函数的性质,可以判断系统的稳定性。该方法不必求解系统的微分方程,就可以直接判断其稳定性。
- 选择一个 Lyapunov 函数
- 求导数
- 稳定: \(V\) 正定,\(\dot{V}\) 半负定;
- 渐进稳定 : \(V\) 正定,\(\dot{V}\) 负定;或者 \(\dot{V}\) 半负定,且 \(x\ne 0\) 时候,\(\dot{V}\) 不恒为 0
- 全局渐进稳定:如果 \(||x||\rightarrow \infty,V(x) \rightarrow \infty\)
- 不稳定:\(\dot{V(x)}\) 正定
V 的寻找 ¶
寻找 v 的过程是一门艺术
- 物理系统:使用能量作为\(V\)函数
满足条件: 1. 对所有的x具有连续的一阶偏导数 2. \(V(x)\)正定
正定性判定: - 西尔韦斯特判据:n阶主子式大于0:正定 - 偶正奇负:负定
lyapunov 方程 ¶
线性定常连续系统的渐进稳定判据
对于任意给定的正定实对称矩阵 \(Q\), 存在正定实对称矩阵 \(P\),使得下列方程成立
可取 \(V(x) = x^T P x\) 为 Lyapunov 函数,有 \(\dot{V} = -x^TQx\)
- 选取 \(Q=I\)
- 带入 lyaponov 方程,求解 \(P\)
- 判断 P 的符号性质

克拉索夫斯基稳定性判据 ¶
系统设计 ¶
能控性 ¶
是否可以从一个点控制到另一个点(不是轨迹控制)
能控性判断 ¶
- \(A\) 是系统矩阵。
- \(B\) 是输入矩阵。
- \(n\) 是系统的状态变量的维数。
通过计算能控矩阵 \(\mathbf{CO}\) 的秩,可以判断系统是否能控。 - 直接求解秩 - 求行列式,不为0,则满秩
Co = ctrb(A,B) # return the controllability matrix
在现实中需要考虑物理因素,所以不一定完全可控
能控标准型变换 ¶
- 首先要注意能控标准型中,最后一行里面系数的顺序
- 其次要注意,构造的是变换矩阵 \(T_c\),而不是 \(T_c^{-1}\)
能控子空间分解 ¶
能控矩阵 \(Rank(Co) = p < n\), 在 \(Co\) 中找出 p 个线性无关的列向量,再配 \(n-p\) 个线性无关的列向量,构成变换矩阵 \(T_c\)
不能控子空间也会对能控子空间产生影响
状态反馈 ¶
拿到一个系统之后,需要先判定这个系统是不是可控的
其中,\(\mathbf{A}\) 的特征值 \(\lambda\)
- \(\lambda\) 的实部决定的了收敛性和收敛速度
- 如果极点是虚数,必定有共轭,且表示有振动
- 状态反馈不会改变系统的零点;不改变不能控子系统的极点;可任意改变能控子系统的极点
- 对于系统 \((A,B)\), 若存在矩阵 K 使得 \((A+BK,B)\) 稳定,则称系统 \((A,B)\) 是可镇定的;
- \((A,B)\) 可镇定的充要条件:\((A,B)\) 的不能控子系统稳定
- 极点任意配置条件:系统完全能控(否则只能在根轨迹线上移动)
- 静态输出反馈控制 \(u=r+Ky = r+KCx\) 不改变能控性和能观性
控制器 u 的两大作用
- 稳定系统
- 调整平衡点
线性控制器:¶
选定 k1 和 k2 \(\rightarrow\) 设计闭环系统 \(A_{cl}\) 的特征值 \(\rightarrow\) 控制系统表现
展开 \(A_{cl}\) 得到特征多项式,与期望极点的特征多项式进行比较,得到 \(k\)
一般步骤
- 确定能控性:写出 Co 矩阵,秩判据
- 直接法:判断矩阵 \(A_{cl}=(A+Bk)\) 的性质
- 间接法:不解 n 个系数方程的方法——化成能控标准型
例子

其中,\(\phi\) 是角度,\(\delta\) 是控制输入,\(g\) 是重力加速度,\(L\) 是摆长。
由于特征值 \(\lambda = \pm \sqrt{\frac{g}{L}}\) 是正实数,因此开环系统是不稳定的。
\(Rank(C_0) =2\), 能控
假设目标是设计一个反馈控制律,使得闭环系统的特征值 \(\lambda_1\) 和 \(\lambda_2\) 都等于 -1。
为了实现这个目标,我们选择一个状态反馈控制律 $ u = - [k_1 quad k_2] begin{bmatrix} x_1 \ x_2 end{bmatrix} $。
闭环系统的特征方程为:
因此,反馈控制律为:
lqr 控制器 ¶
如何确定 \(\lambda\), 什么样的 \(\lambda\) 是最优的?
引入 cost function:
在满足稳定性的情况下,找到 cost function 的最小值
- Q 侧重于系统状态
- R 更侧重于控制器输入
理解 u
u 是控制器的输入,随着系统输出 x 的变化而变化,所以可以看作是闭环的系统
理论上,u 可以随便选,但实际应用当中要考虑执行器的情况。比如自动驾驶场景,输入 u 是方向盘的角度,就是有界的。
阿克曼公式 ¶
不需要系数对应
能观性 ¶
卡尔曼与能观性
Kálmán published several seminal papers during the sixties, which rigorously established what is now known as the state-space representation of dynamical systems. He introduced the formal definition of a system, the notions of controllability and observability

卡尔曼滤波器就是随机系统的状态观测器
能观性判断 ¶
- 直接求解秩
- 求行列式,不为 0,则满秩
能观标准型构造 ¶
要注意的是能观标准形的转化是先求 \(T_o^{-1}\)
能观子空间的分解 ¶
从能观矩阵 \(Q\) 中找出 \(n-p\) 个线性无关的行向量,配 \(p\) 个线性无关的行向量,构成变换矩阵 \(T_o^{-1}\)
观测器 ¶
全维观测器(luenberger observer 龙贝格)¶
通过系统的输入和输出来估计系统的状态
实际上,建立新的反馈系统,使得 \(e_x = x - \hat{x} \to 0\)

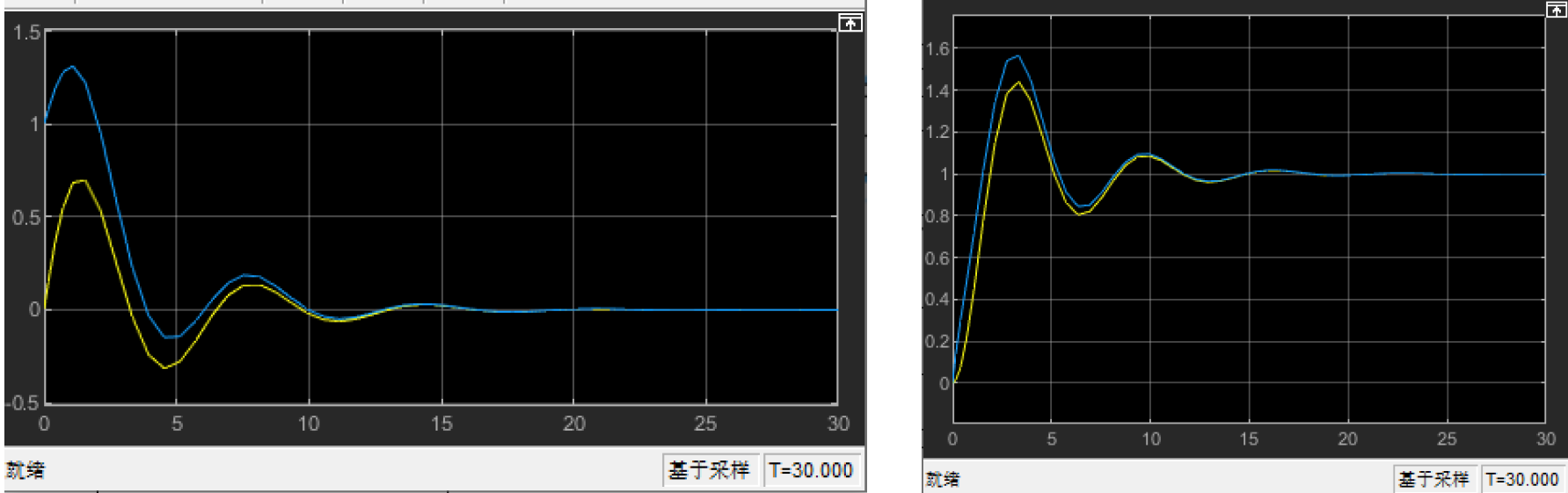
推导过程
设 \(\hat{x}\) 为估计值,\(\hat{y}\) 为估计的输出
代入 3
1-5, 代入②
令 \(x-\hat{x}= e_x\),error 误差,是估计值与实际值间的误差
目标 \(e_x \to 0\)
降维观测器 ¶
分离原理 ¶
最好观测器的收敛速度要比控制器要快,需要有一个准确的观测的值指导控制器的输入