数电 ¶
约 3636 个字 预计阅读时间 14 分钟
数字电子技术(余孟尝)思维导图 - 知乎 (zhihu.com)
数制和码制 ¶
进制与进制转换 ¶
2,4,16
- x 变 10:多项式加法
- 10 变 2:模二取余法
- 2 变 16:隔 4 位合并
- 16 变 2:每位拆成 4 位二进制
- 其他:通过二进制间接变换
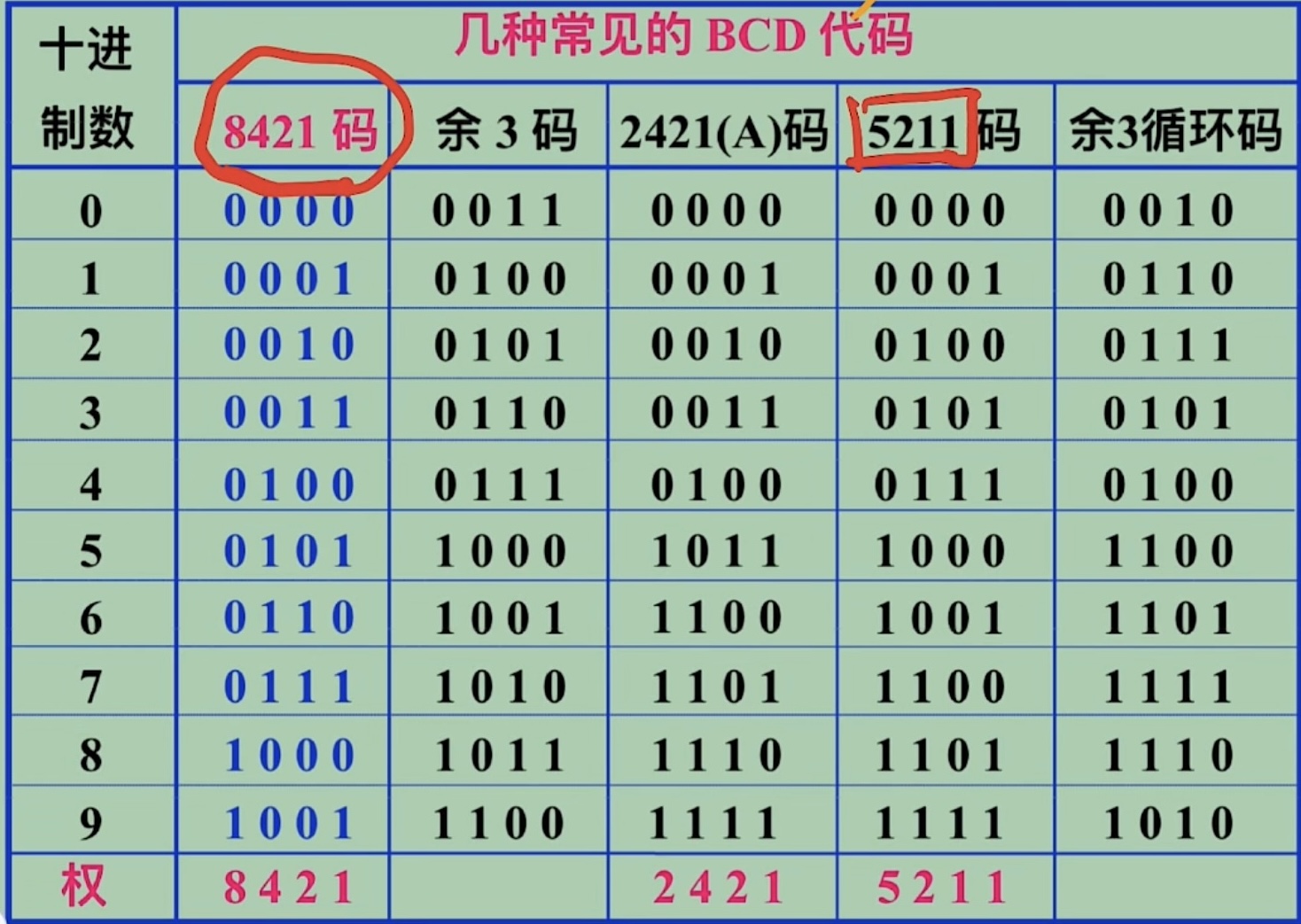
其他码值(不同权值)¶
运算 ¶
- 移位和相加
- 反码
- 补码
- 最高位符号位:0 正 1 负
- 正数不变,负数反码 +1
为什么要采用反码和补码??( 参考这篇知乎文档 )
采用同余的思想,用加法完成减法的任务
在这里,再次强调原码、反码、补码的引入是为了解决做减法的问题。在原码、反码表示法中,我们把减法化为加法的思维是减去一个数等于加上这个数的相反数,结果发现引入符号位,却因为符号位造成了各种意想不到的问题。
但是从上面的例子中,可以看到其实减去一个数,对于数值有限制、有溢出的运算(模运算)来说,其实也相当于加上这个数的同余数。
也就是说,不引入负数的概念,就可以把减法当成加法来算。
由补码求原码:
- 先取反,再加一
- 先减一,再取反
门电路 ¶
门电路中以高 / 低电平表示逻辑状态的 1/0
正逻辑:高电平表示 1,低电平表示 0 负逻辑:高电平表示 0,低电平表示 1
二极管门电路 ¶
与门 ¶

使用优先导通原理
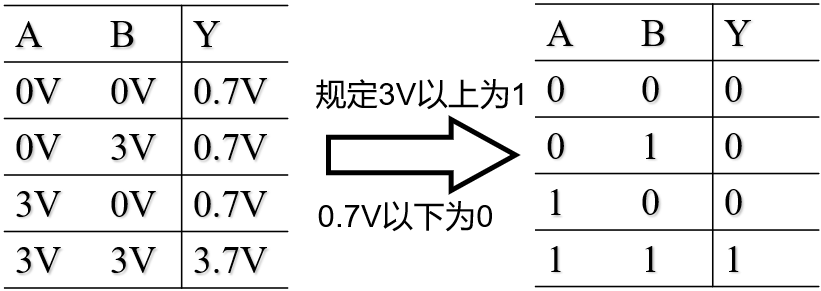
或门 ¶

- 二极管构成的门电路的缺点
电平有偏移,带负载能力差
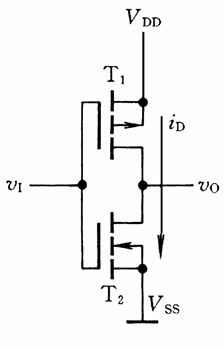
MOS 管门电路 ¶
电路具体实现

TTL 门电路 ¶


只要参数合理: $$ begin{align} V_I = V_{IL},T截止,V_o = V_{OH}\ V_I = V_{IH},T导通,V_o = V_{OL} end{align} $$ 三极管的基本开关电路就是非门
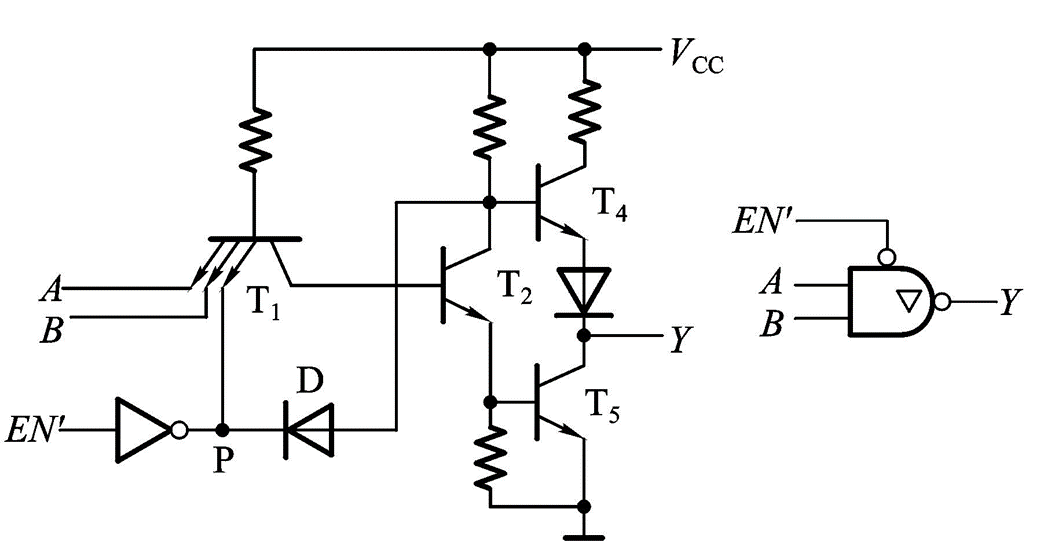
三态输出门(Three state Output Gate ,TS)¶
TTL 集成与非门 ¶

组合逻辑电路 ¶
功能上:输出仅与该时刻的输入有关,与控制电路没有关系
结构上:由门电路组成,不含记忆(存储)元件。
对每个器件,分析清楚基本功能和扩展方法
设计方法 ¶
一、逻辑抽象
- 分析因果关系,确定输入 / 输出变量
- 定义逻辑状态的含意(赋值)
- 列出真值表
二、写出函数式
三、选定器件类型
四、根据所选器件:对逻辑式化简(用门
五、画出逻辑电路图,或下载到 PLD
分析方法 ¶
- 从输入级开始,逐级写出门的逻辑表达式
- 对表达式进行化简
- 列真值表
- 描述电路的逻辑功能



加法器 ¶
半加器 ¶
不考虑来自低位的进位,将两个 1 位的二进制数相加
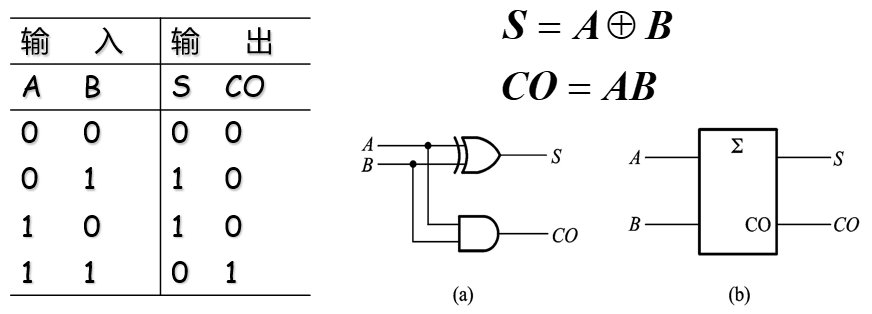
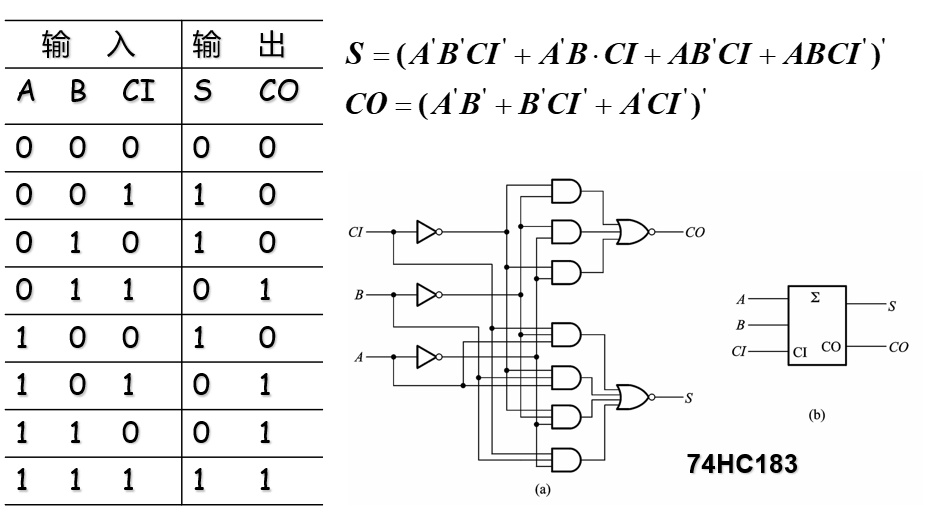
全加器 ¶
将两个 1 位二进制数及来自低位的进位相加
多位加法器 ¶
1. 串行进位加法器
优点:简单;缺点:慢

2. 超前进位加法器
预测进位信息

基本原理:加到第 \(i\) 位的进位输入信号是两个加数第 \(i\) 位以前各位 \(0 \ to\ i-1\)的函数,可在相加前由 A,B 两数确定。


可以使用 4 个 4 位超前进位加法器组成一个 16 位的超前进位加法器


比较器 ¶
从高到低比较
一位比较 ¶
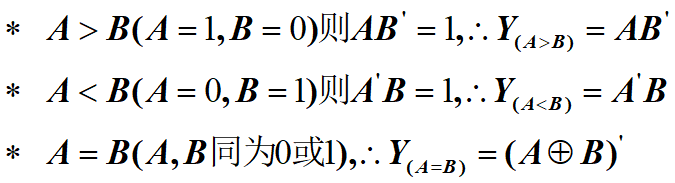

推导:最上面一条支路函数使用德摩根定律进行化简:
\(A\cdot \bar{AB} = A \cdot (\bar{A} + \bar{B}) = A\cdot\bar{B}\)
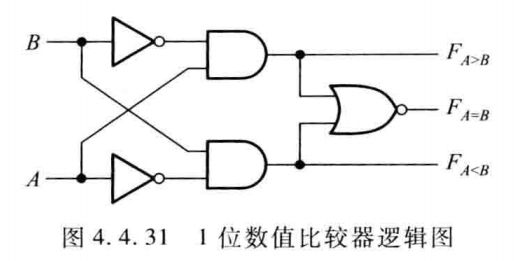
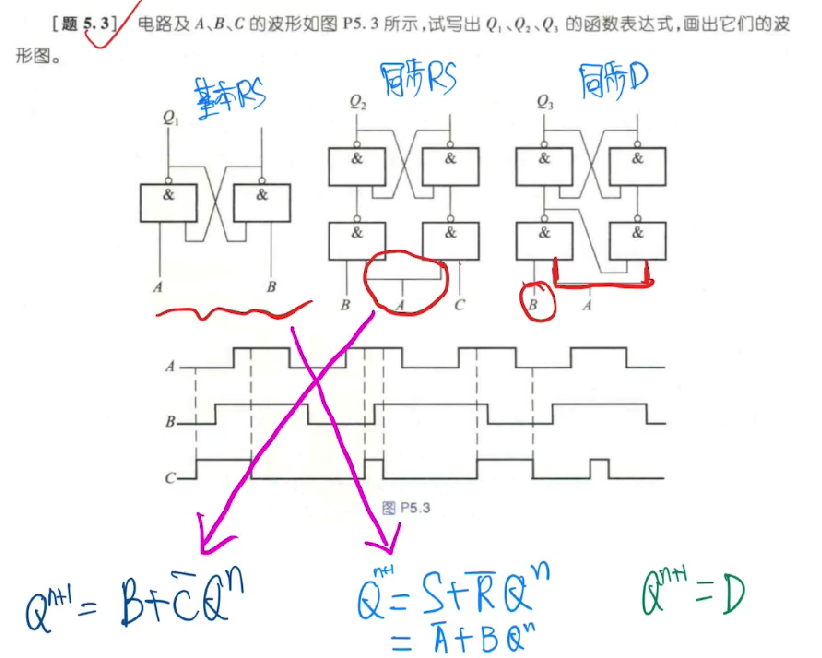
先实现一位比较,写出逻辑表达式,再给出逻辑图。
注意或非门的画法
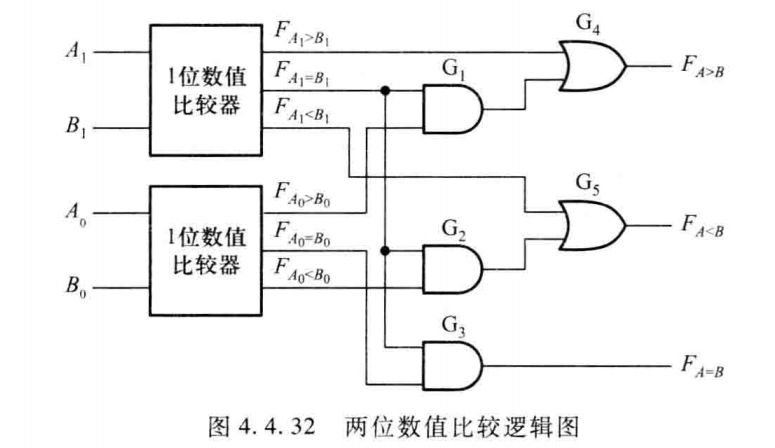
两位比较 ¶

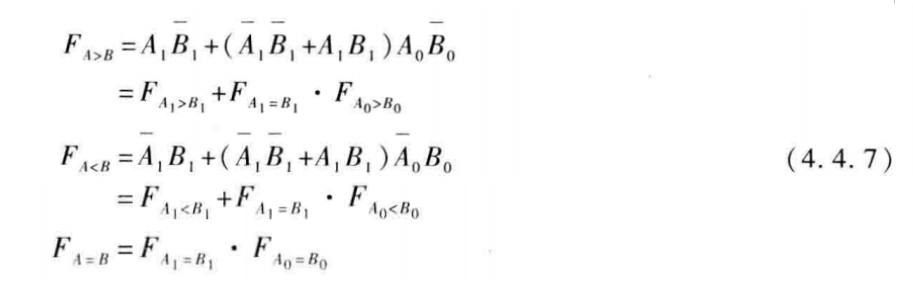
CC14585¶
实现 4 位二进制数的比较

这是为什么 为什么采用这种方式
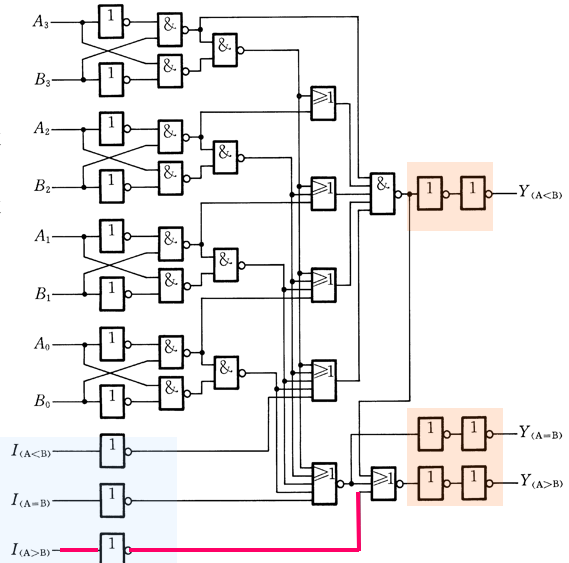
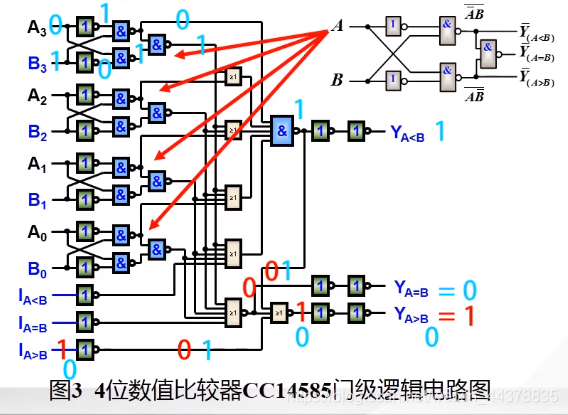
- 多位比较
级联方式:串联 and 并联
串联需要将后 4 位的比较结果作为输入,最低一级要将 \(I_{A=B} = 1,I_{A>B}= I_{A<B} = 0\)
相当于串一个第零级比较器,且第零级比较结果是相同,所以要比高位
\(I_{A=B},I_{A>B},I_{A<B}\) 称为扩展输入端,为了传递低位的比较结果,便于级联
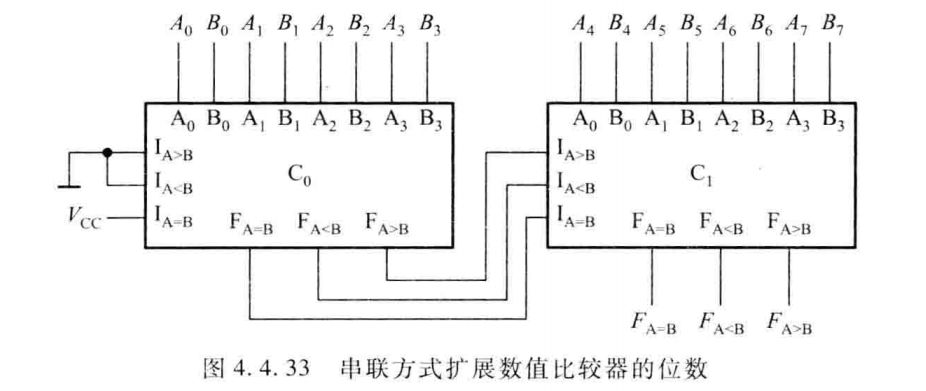
并联用于位数比较多,且对速度有要求的时候。
由图可以看出这里采用两级比较方法,将 16 位按高低位次序分成四组,每组 4 位,各组的比较是并行进行的。将每组的比较结果再经 4 位比较器进行比较后得出结果。
显然,从数据输入到稳定输出只需 2 倍的 4 位比较器延迟时间,若用串联方式,则 16 位的数值比较器从输入到稳定输出需要约四倍的 4 位比较器的延迟时间。
编码器 ¶
本节参考了写的非常清楚的一篇笔记——自上而下理解优先编码器
- 编码:是将信息从一种形式或格式转换为另一种形式的过程。在数字电路中,用预先规定的方法,将一些逻辑信号转换成二进制数代码,这个过程就称为编码。
- 编码器:实现编码这一过程的集成组合逻辑电路器件。
普通编码器 ¶
任何时刻只允许输入一个编码信号

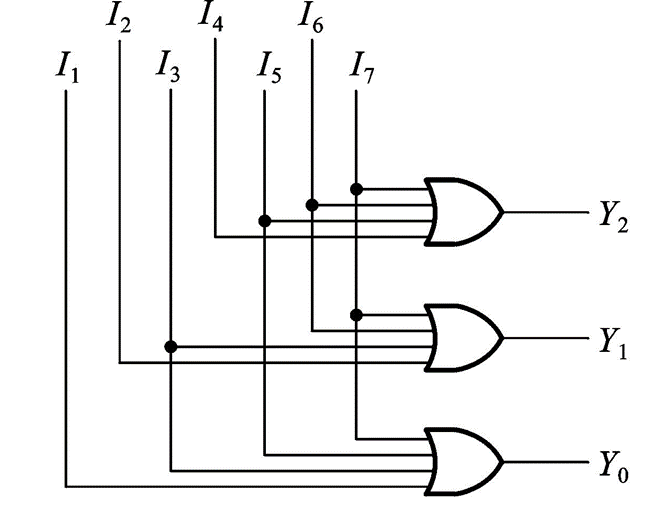
优先编码器 74LS148 ¶
普通编码器的输入端只能同时存在一个高电平信号,当我们不小心输入了多个高电平信号,比如输入 (11111111),根据电路图普通编码器输出的结果为 (111), 与正常输入 (00000001) 的结果相同,但我们从输出端根本无法判断输入了一个错误的信号。
允许同时输入两个以上的编码信号,但只对其中优先权最高的一个进行编码。
为什么使用反逻辑
高电平容易受到干扰,所以如果采用高电平有效的方式,那么很容易在低电平上产生高电平噪声;
相反,如果采用低电平有效,出现误有效的情况概率就很低了
要非常注意低电平有效时候,输出的问题。
“对人说人话(真值),对鬼说鬼话(编码)”
为了表示输入方式为低电平有效,对于输入变量的书写我们加上一个非号,例如原来的高电平有效的 \(I_7\) ,写成 \(I_7'\) 来表示低电平有效。
假设一块 8 线编码器的 8 个输入分别为 \(I_{15}' \dots I_8'\),另一块为 \(I_{7}' \dots I_0'\),当 \(I_{15}' \dots I_8'\) 输入均为 1 时,再启用第二块 8 线编码器。
这里存在两个问题
- 一个是如何让第二块编码器知道被自己启用了:我们对 8 线编码器增加一个输入开关 \(S'\), 用以控制编码器的工作状态;\(S' = 1\) 时候,高电平无效,第二块编码器就不启动,输出均为 1;
- 另一个这是如何让第一块编码器传递均是无效输入的信息:我们对 8 线编码器再增加一个输出端 \(Y_s'\),当输入全为 1 时, \(Y_s'\) 输出为 0,用以开启第二块编码器的开关。即,\(Y_s'\)表示第一块都是 1(都无效)
什么意思

在尝试连接过程中,又有一个新问题,16 线 -4 线比起 8 线 -3 线多了 8 个输入端,却只多了一个输出端,这是为什么呢 ?
4 位二进制数正好能表示 \(0-15\),而后三位足以表示 \(0-7\),也就是说,当输入结果仅在 \(0-7\) 时,靠第二块编码器的 3 位输出足以表示,只用输入结果在 \(8\) 的以上的信号时,才用到第一块编码器,并且这 4 位二进制数的第一位肯定为 1,换言之,只要用到 \(I_{15}' \dots I_8'\), 第四位肯定为 1
因此,我们不妨再添加一位输出位 \(Y_{EX}'\),传递是否用到该编码器的信息,当编码器存在有效输入信号时,输出结果为 0。这样,新增的这个输出端可以直接用于 4 线输出端的最高位输出。

注意 74LS148 输入输出都是低电平有效
普通编码器和优先编码器的区别
普通编码器只能有一个请求
优先编码器可以有多个请求,但是事先规定了优先级
译码器 ¶
译码:是编码的逆过程。把一些二进制代码所代表的特定含义“翻译”出来的过程叫做译码
将每个输入的二进制代码译成对应的输出高、低电平信号
二进制译码器 ¶
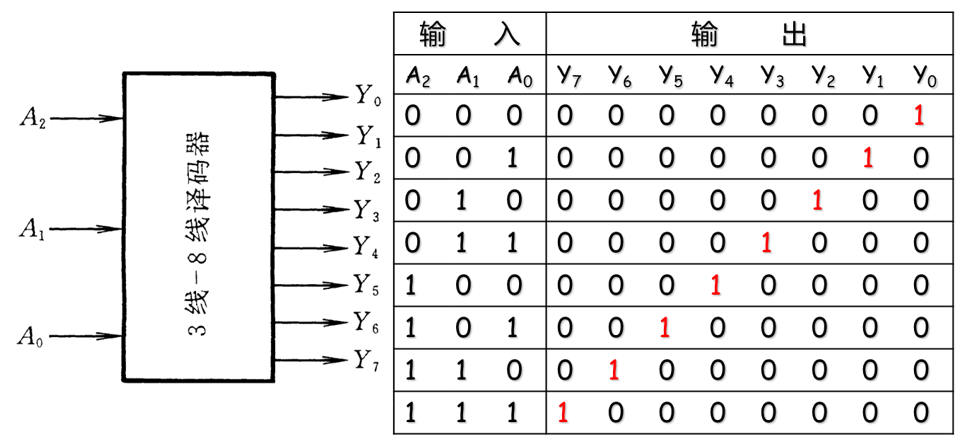


把连续的地址空间变成连续的八片
使用负逻辑的原因
注意:图中没有直接利用原输入信号,而是经过了两个非门,右重新得到了 1 个一模一样的信号,这样做的目的是增大电流,即增强信号本身带负载的能力,即允许电流的大小。
在集成运放部分中曾介绍过电压跟随器,其输入与输出相同,但带载能力更强。在上述电路中有 2 个非门,就相当于电压跟随器,虽然信号电平没有变,但后面与门所需要的电流来自非门的电源,而不是来自输入信号本身,因此可以带更多的负载,例如上述电路中就携带了 4 个与门。
另外,由于门电路的内部电路自身的特性,在其输出低电平时,可以允许通过更大的电流,即带载能力更强,因此更多的选择低电平作为有效的逻辑电平,即低电平有效。
74LS138¶
输入高电平,输出低电平。
输入选通控制端
- 芯片正常工作 \(S_1 = 1 \ and\ \bar{S_2} + \bar{S_3} = 0\)
- 芯片禁止工作 \(S_1 = 0 \ or\ \bar{S_2} + \bar{S_3} = 1\)
注意低电平输出要取反
显示译码器 ¶
数据选择器 ¶
并行 to 串行
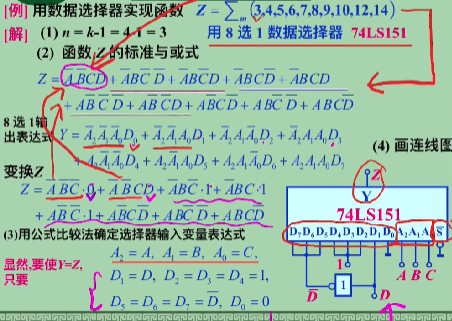
74LS151 八选一
输入端 D
状态控制端 A
输出端 Y
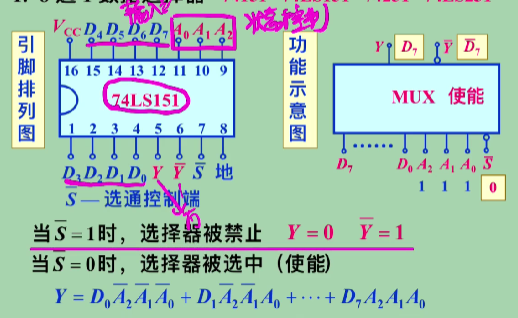
级联形式
当输入 0xxx,左边用不了,只能记录 0~7
当输入 1xxx,右边用不了,记录 8~15

公式比较法
-
选择数据选择器的位数,等于 \(变量数-1\)
-
写出标准与或式,最小项的和
- 令状态控制端分别等于 ABC
- 分别与标准与或式进行逐项对比,获得输入的系数即可

数据分配器 ¶
串行 to 并行
1 路输入,传输到 n 个输出端
74LS138 译码器 作为数据分配器

竞争与冒险
电路存在延时,电路飘忽不定,使组合逻辑电路出现竞争与冒险
不存在集合相邻则无竞争冒险
引入封锁脉冲
引入选通脉冲
触发器 ¶

基本要求
-
有两个稳定的状态 0,1,以表示存储内容
-
能够接收、保存和输出信号。
现态:\(Q^n\) 触发器接收输入信号之前的状态
次态 \(Q^{n+1}\) 触发器接收输入信号之后的状态
要求
会认符号,能从电路图对应触发器
掌握输出表达式
基本触发器 ¶
基本 RS 触发器
\(Q^{n+1} = S +\bar{R} \cdot Q^n\)
同步触发器 ¶
注意记忆电路组成状态
多一个脉冲控制端 $$ begin{align} when CP = 0: &bar{S} = bar{R} = 1,\&Q^{n+1} = Q^{n}\ when CP = 1: &overline{S cdot CP} = overline{Scdot 1} = bar{S}\ &overline{Rcdot CP} = overline{Rcdot 1} = bar{R}\ &与基本触发相同 end{align} $$ 同步 RS
多了一个控制端,多了一个约束条件 $$ left{ begin{aligned} &Q^{n+1} = S+bar{R}cdot Q^n\ &RS = 0(约束条件) end{aligned} right. $$
同步 D
把 R,S 连接成 D $$ left{ begin{aligned} &Q^{n+1} = D\ & CP = 1 end{aligned} right. $$ 考点:脉冲锁存
CP = 0,状态不变
CP = 1,状态跟随
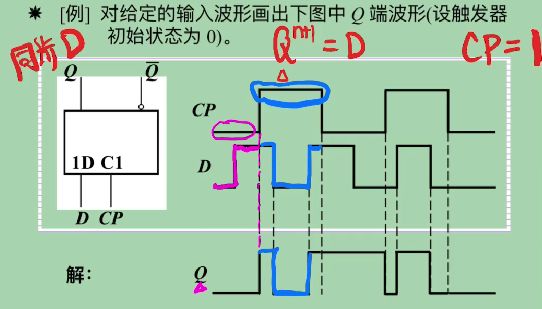
存在问题:触发方式可能会出现空翻
空翻:\(CP = 1\) 期间,触发器发生两次及以上的翻转。
为保持电路稳定工作,要求在一个 CP 脉冲期间,触发器只能动作一次
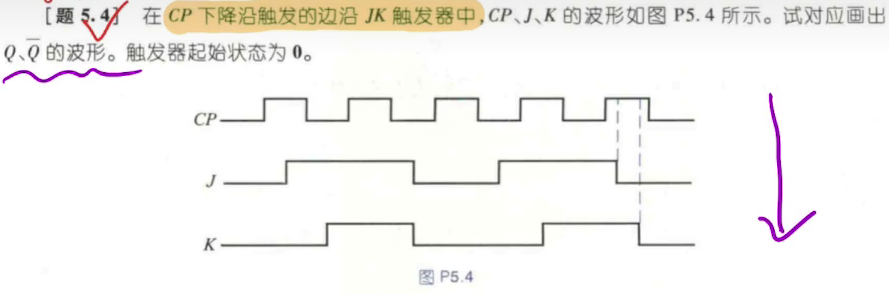
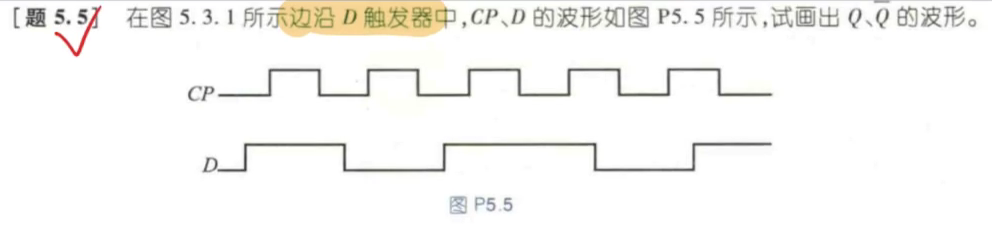
边沿触发器 ¶
只能在脉冲变化沿改变

上升 or 下降有效?
观察 CP 端是否有非门
脉冲没来:初值设置方法:异步 D
异步端控制初值
例题

下降沿跟随
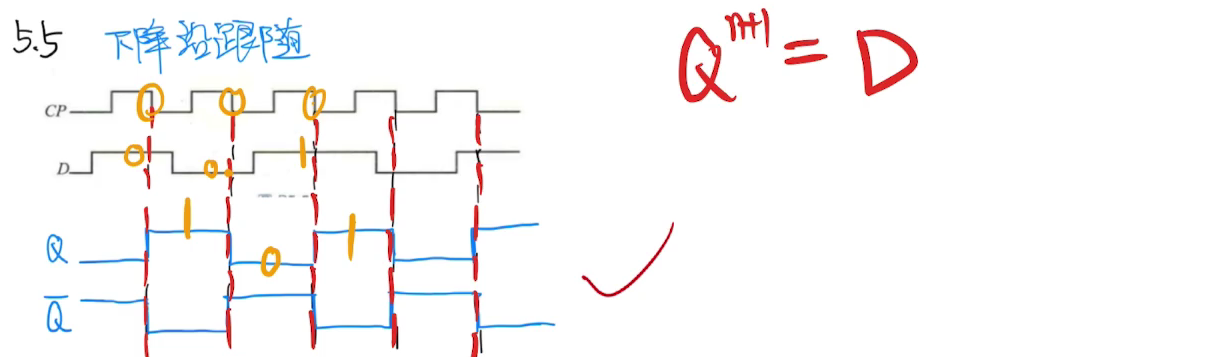
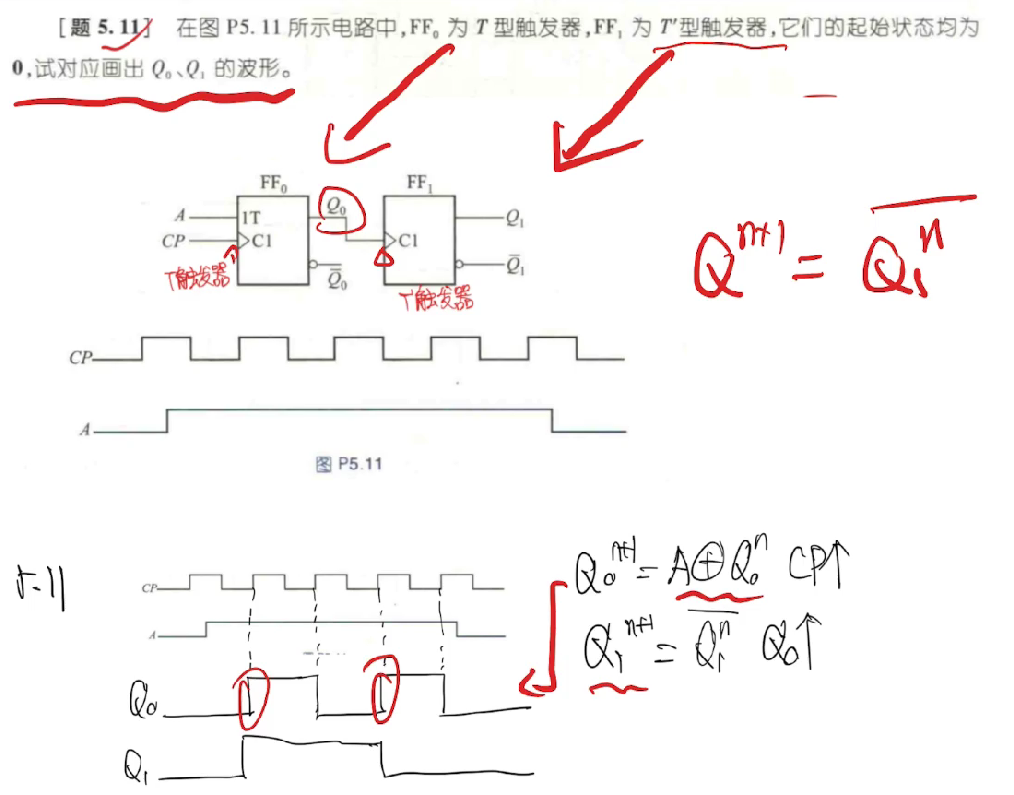
时序逻辑电路 ¶

任何时刻电路的输出不仅与输入信号有关,还取决与电路原来的状态
分析 ¶
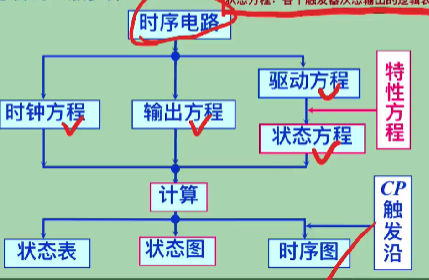
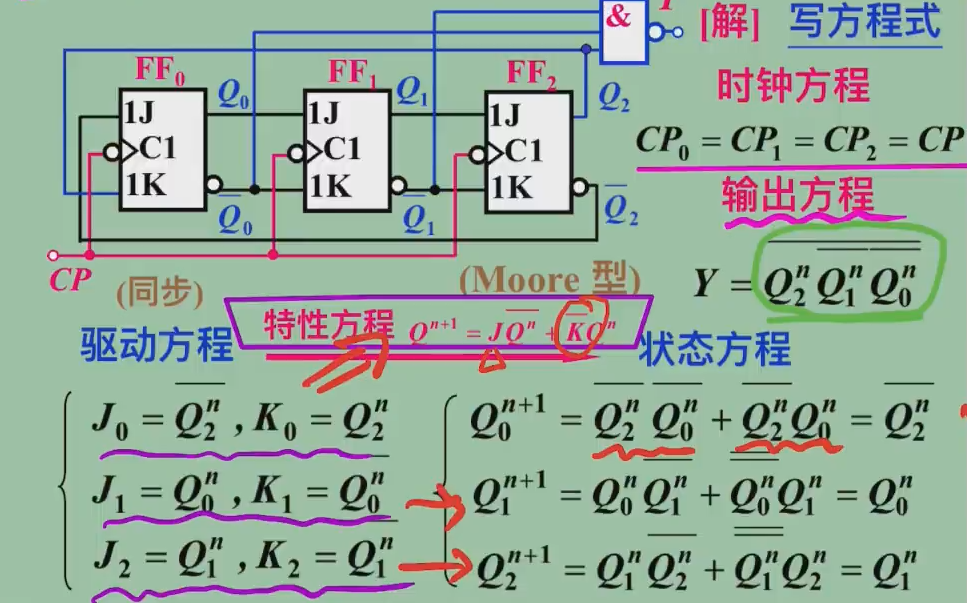
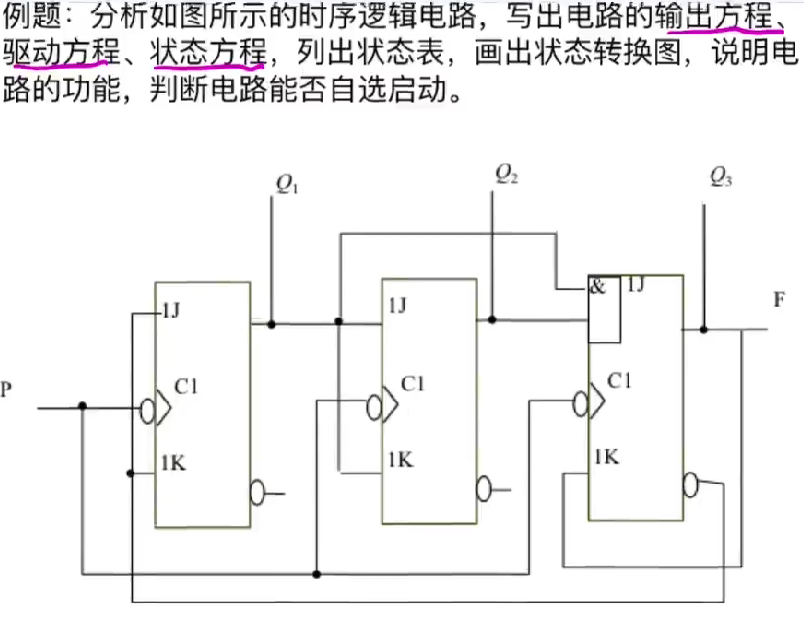
写方程 ¶
时钟方程:各个触发器时钟信号的逻辑表达式
CP = balab
输出方程:电路各输出信号的逻辑表达式
Y = dafasdf
驱动方程:各触发器输入信号的逻辑表达式
触发器是怎么驱动的
状态方程:各个触发器次态输出的逻辑表达式
列状态 ¶
状态表:真值表
状态图
时序图
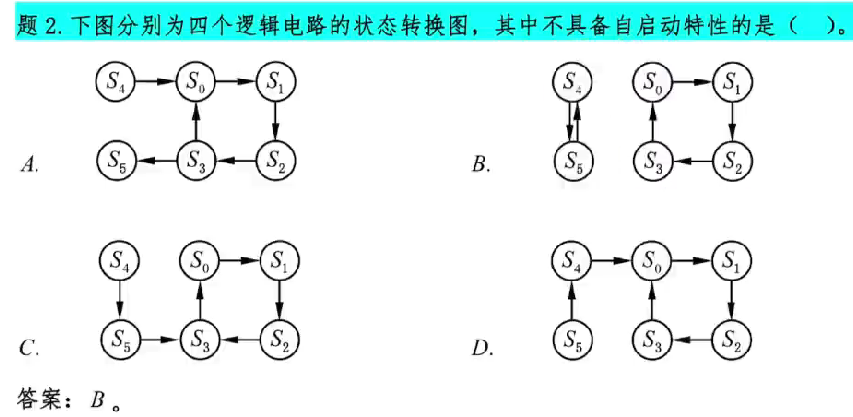
说功能 ¶
- 功能
- 是否自启动
能自启动:存在无效状态,但是没有形成循环
不能自启动:无效状态形成循环
注意
时序电路的现态是指组成该电路各个触发器现态的组合计算时,不能漏掉任何可能出现的现态和输入取值 ;
现态的起始值如果给定了,则可以从给定值开始依次进行计算,若未给定,可以从自己设定的起始值开始依次计算 ;
状态转换图或状态表描述的是整个时序电路各状态之间的转换关系
状态转换总是由现态转换到次态
输出是现态和输入的函数,不是次态和输入的函数
设计 ¶

分类 ¶
同步 / 异步 ¶

输出信号特性 ¶
Moore¶
Mealy¶
计数器 ¶
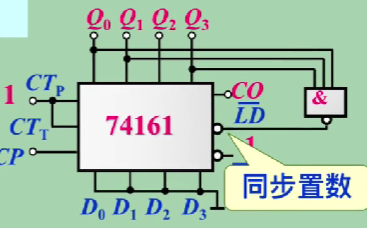
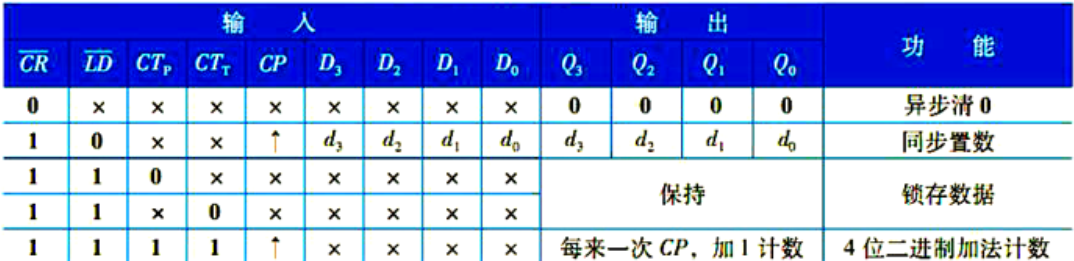
核心:置数、清零
同步并行置数 到 \(S_{N-1}\)
同步清零:到 \(S_{N-1}\)
计数只能记到进制 -1;eg:十进制只能记到 9
异步清零:到 \(S_{N}\)
可以一直记到进制;eg:十二进制记录到 12
保持:
计数:
CP 变化时候,进行计数

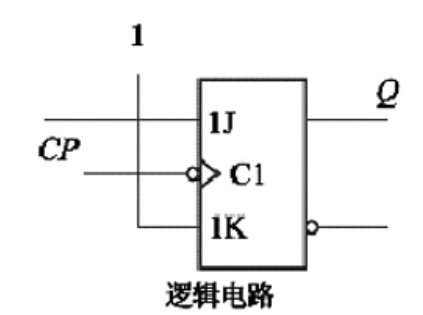
二进制计数器
利用 JK 触发器
n 位二进制计数器
74LS161——同步置数,异步清零,低电平有效
74LS163——同步置数,同步清零
十进制计数器
使用二 - 十进制(BCD 码)
74LS160——同步置数,异步清零
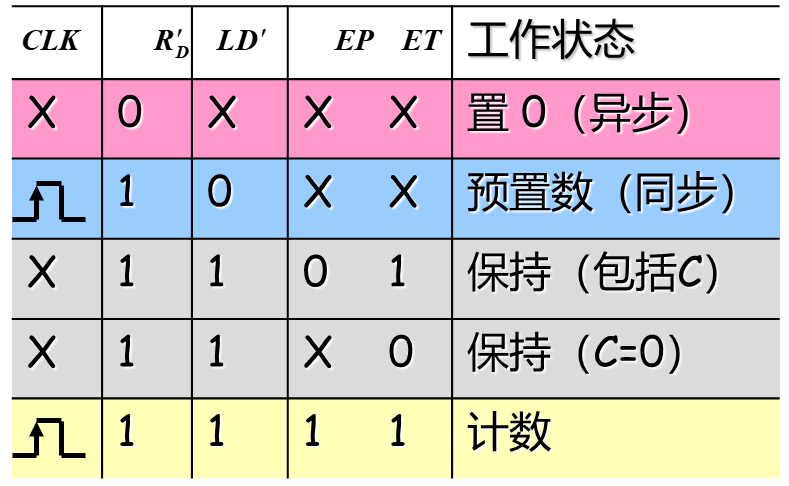
74LS162——同步置数,同步清零
n 进制计数器
- 写出状态 \(S_{N-1}\) 的二进制代码
- 求归零逻辑表达式
- 画出连线图
大容量 N 进制计数器
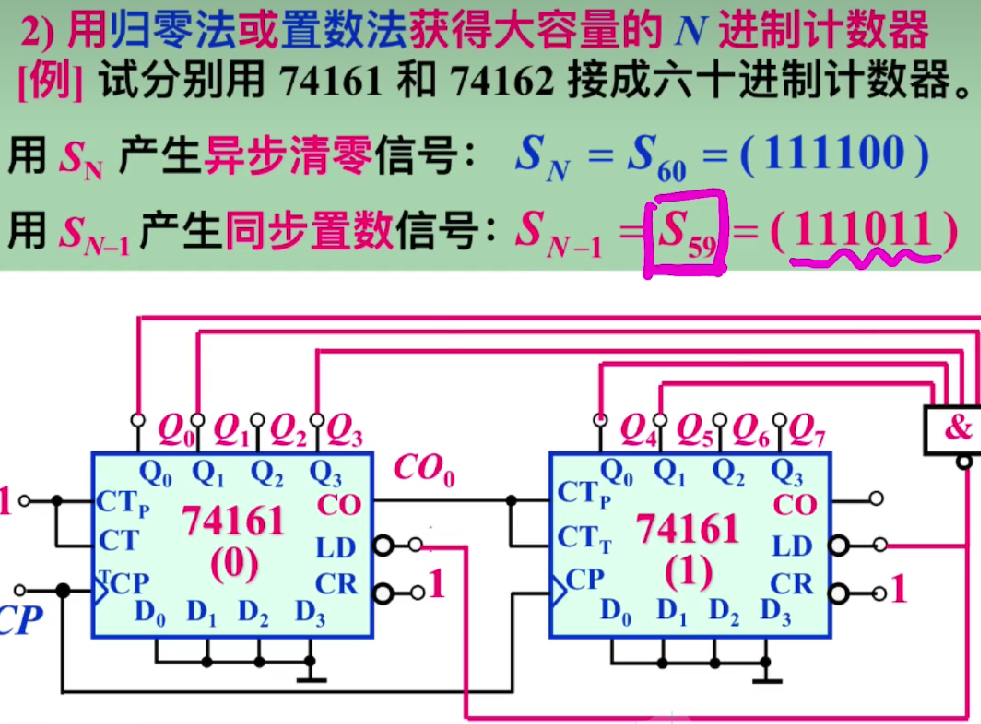
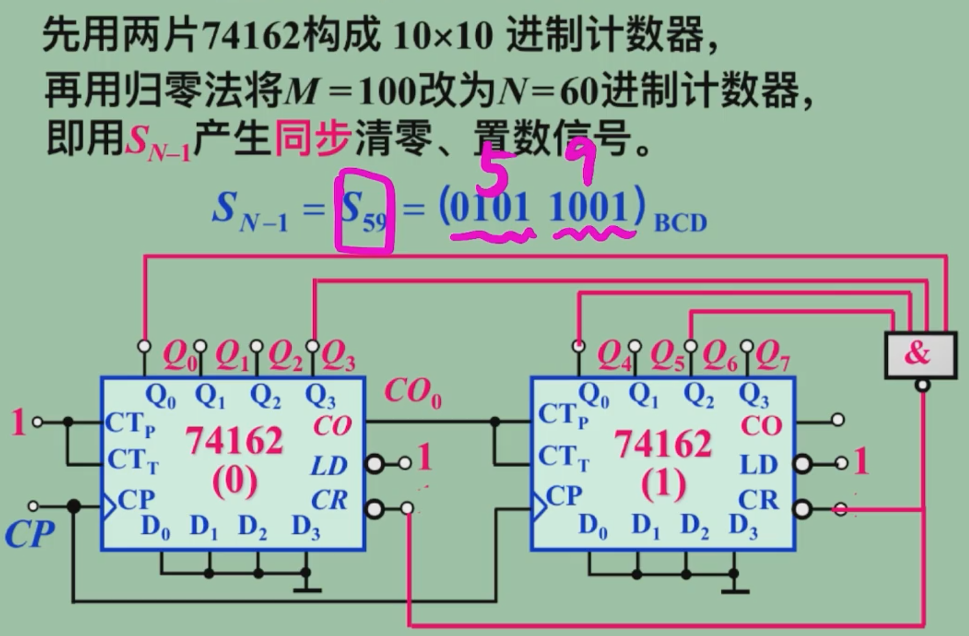
右侧是十位、左侧是个位

寄存器 ¶
移动寄存器——必须是边沿触发器
右移:按照 \(Q_0Q_1Q_2Q_3\) 的顺序
串行输入、并行输出

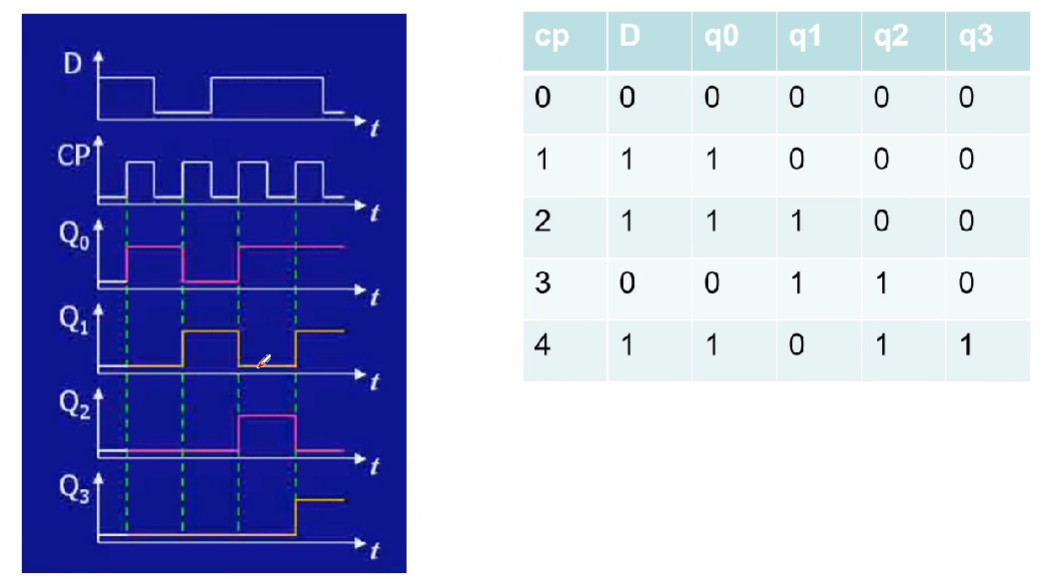
左移:按照 \(Q_3Q_2Q_1Q_0\) 的顺序
读写存储器 ¶
例题 ¶
自启动