数电 ¶
约 703 个字 15 张图片 预计阅读时间 3 分钟
逻辑电路 ¶
| 符号 | LaTeX 表示 | 公式示例 | 说明 |
|---|---|---|---|
| 与(AND) | \land |
\(A \land B\) | 逻辑与运算符 |
| 或(OR) | \lor |
\(A \lor B\) | 逻辑或运算符 |
| 非(NOT) | \neg |
\(\neg A\) | 逻辑非运算符 |
| 蕴含(IMPLIES) | \rightarrow |
\(A \rightarrow B\) | 逻辑蕴含运算符 |
| 等价(EQUIVALENT) | \leftrightarrow |
\(A \leftrightarrow B\) | 逻辑等价运算符 |
| 全称量词(FOR ALL) | \forall |
\(\forall x \, P(x)\) | 全称量词 |
| 存在量词(THERE EXISTS) | \exists |
\(\exists x \, P(x)\) | 存在量词 |
| [ 真值表与逻辑表达式 | 由逻辑表达式列真值表 |
\[
Y = A\quad AND\quad B = A\&B = A\cdot B = AB
\]
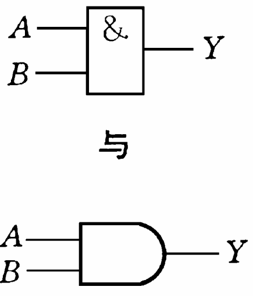
\[
Y = A \quad OR \quad B = A+B
\]
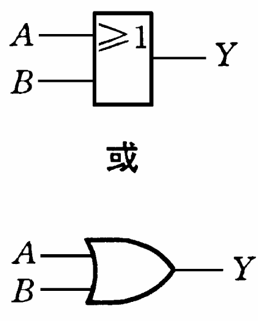
\[
Y = A' = NOT \quad A
\]
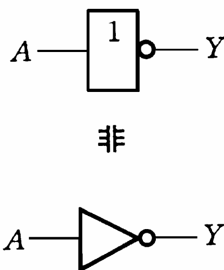
不同则为 1,相同则为 0
不进位的加法
\[
Y = A \oplus B = \bar{A}B + A\bar{B}
\]
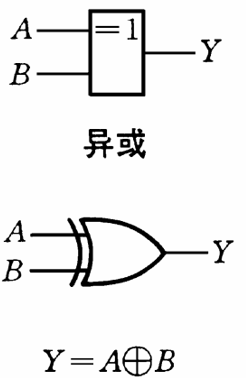
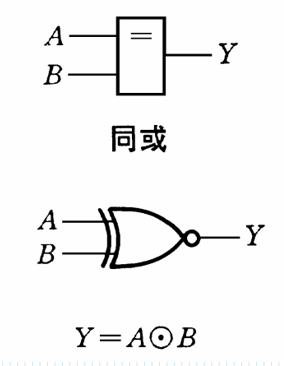
不同则为 0,相同则为 1;
\[
Y = A \odot B
\]
基本公式 ¶
常量与常量 ¶
\[
\begin{align*}
1 + 1 = 1\\
0\cdot0 = 0
\end{align*}
\]
常量与变量 ¶
\[
\begin{align*}
A \cdot 0 = 0\\
A+1 = 1\\
\end{align*}
\]
变量和变量 ¶
分配律
$$
A+BC = (A+B)(A+C)
$$
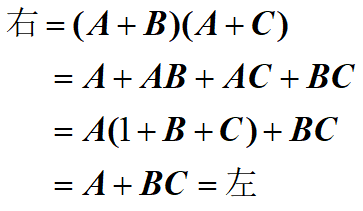
同一律
\[
\begin{align*}
A+\bar{A} = 1\\
A\cdot \bar{A} = 0\\
\\
A\cdot A = A\\
A + A = A
\end{align*}
\]
反演律(De Morgan's laws)
并项法
\[
AB + A\bar{B} = A
\]
吸收法(短项吸收长项)
\[
\begin{align*}
A + AB = A(1+B)= A\\
AB + \bar{A}C + BC = AB + \bar{A}C
\end{align*}
\]
消因子(短项能够消去 长项中 的 相反项)
\[
\begin{align*}
A+\bar{A}B = A+B\\
A\cdot (1+B) = A+AB+A’B = A+B
\end{align*}
\]
配项法
\[
\begin{align*}
A + \bar{A} = 1\\
A \cdot A = 0
\end{align*}
\]

逻辑函数化简 ¶
逻辑式、逻辑图、波形图
规则 ¶
1. 反演规则:与或互换,01 互换;原变量变成反变量,反变量变成原变量
2. 对偶规则:与或互换,01 互换
3. 标准与或式:\(n\) 个变量,共有 \(2^n\) 种可能 eg. 三变量逻辑函数 \(Y = A+BC\) 的最小项表示为 \(\Sigma m(3,4,5,6,7)\)
4. 与非 - 与非表达式:化成与或式;两次取反;德摩根定律
公式化简 ¶
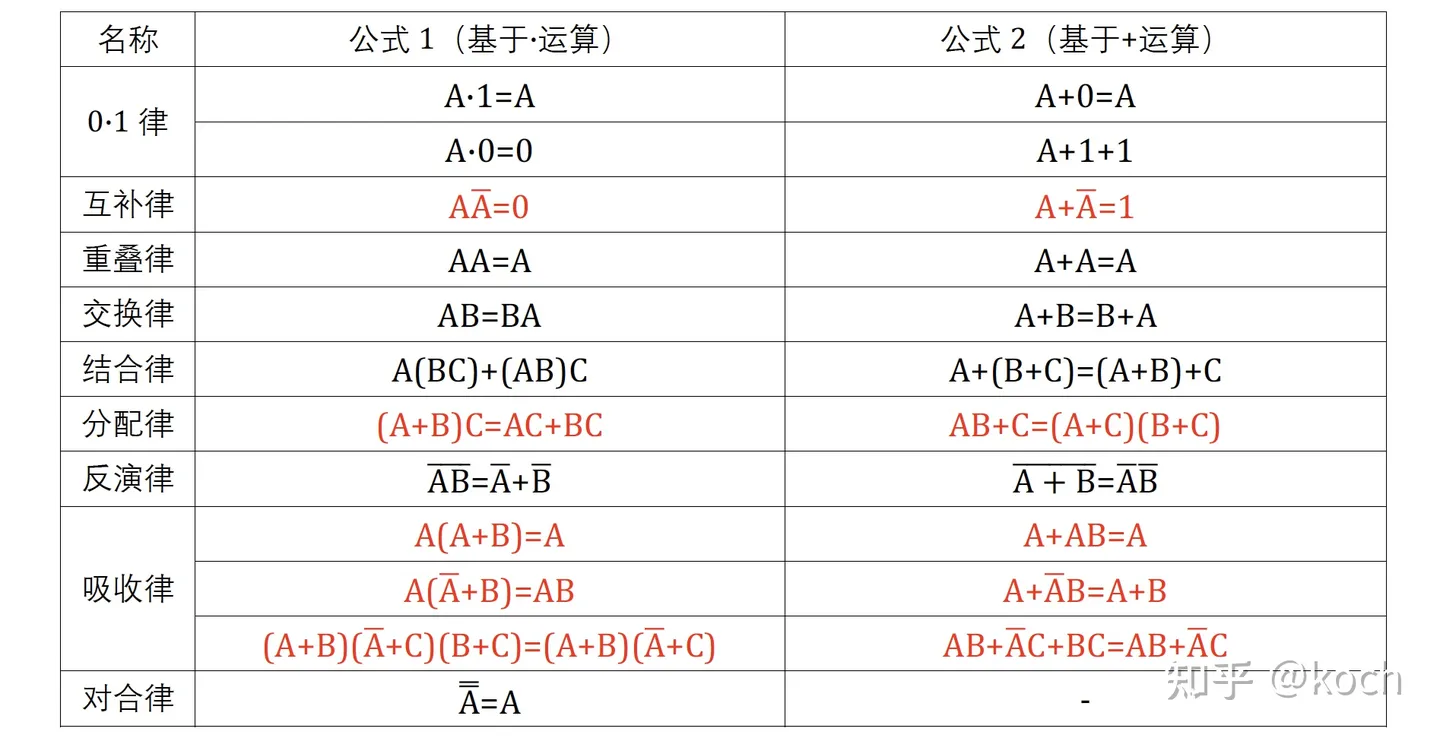

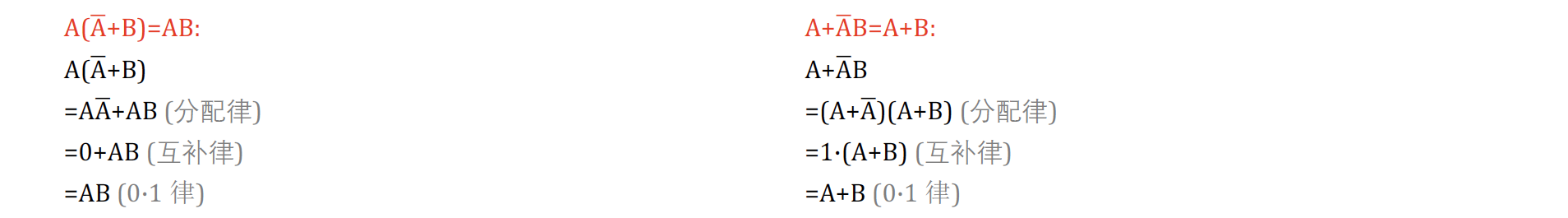

真值表 ¶
由真值表写逻辑表达式
第一步:从真值表内找输出端为“1”的各行 , 把每行的输入变量写成乘积形式 ; 遇到“0”的输入变量上加非号。
第二步:把各乘积项相加 , 即得逻辑函数的表达式。
卡诺图 ¶
用几何相邻表示逻辑相邻(两个最小项只有一个变量不同)
所以顺序是 00,01,11,10
化简:相邻、相对(偶数个
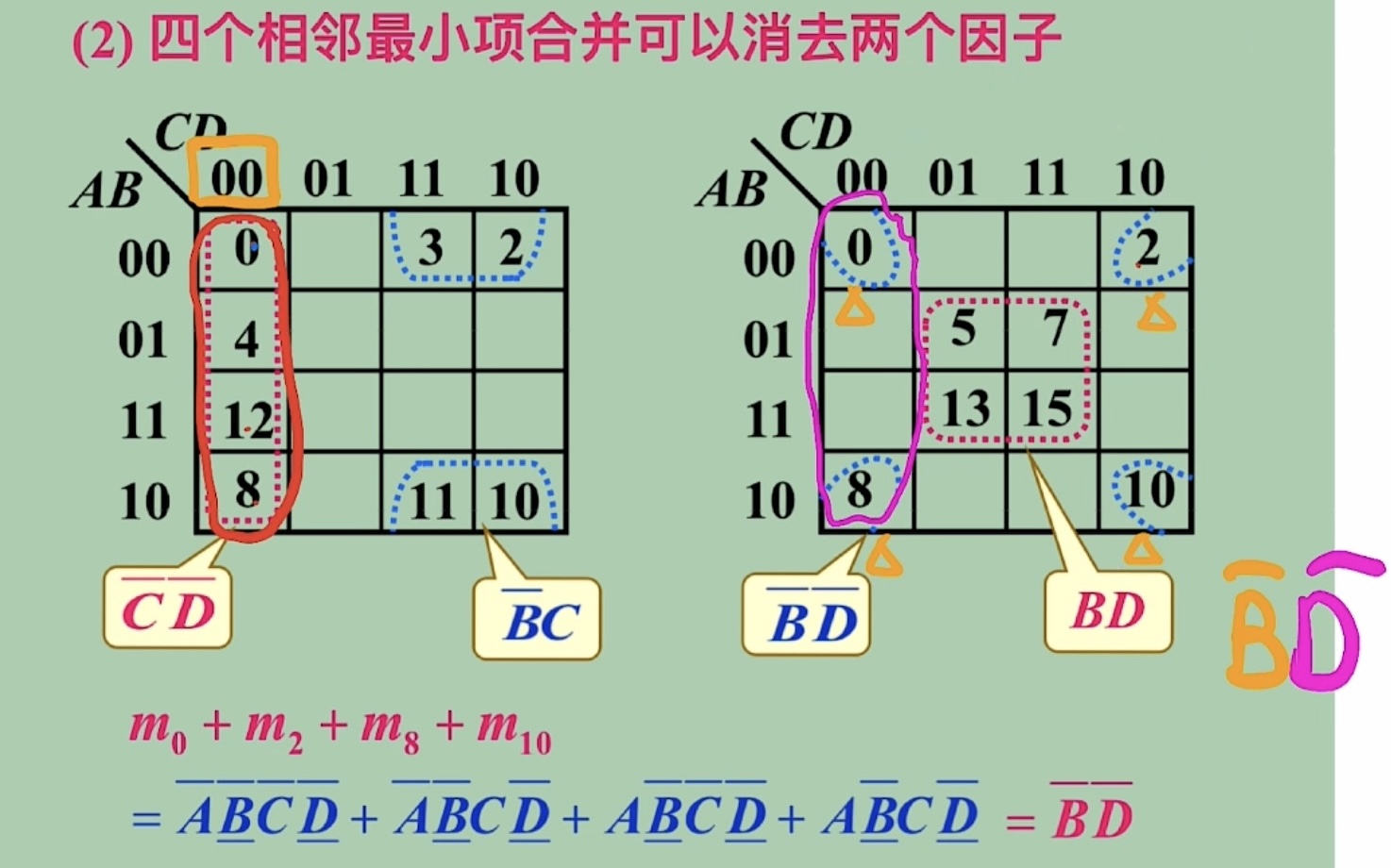
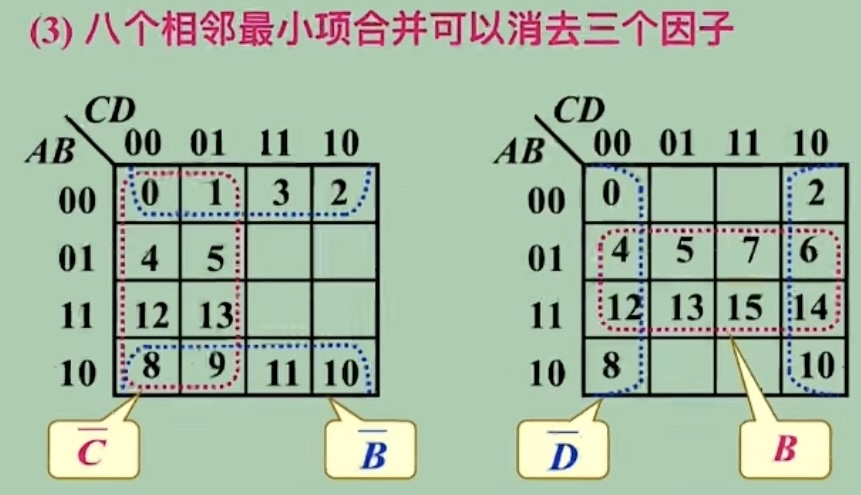
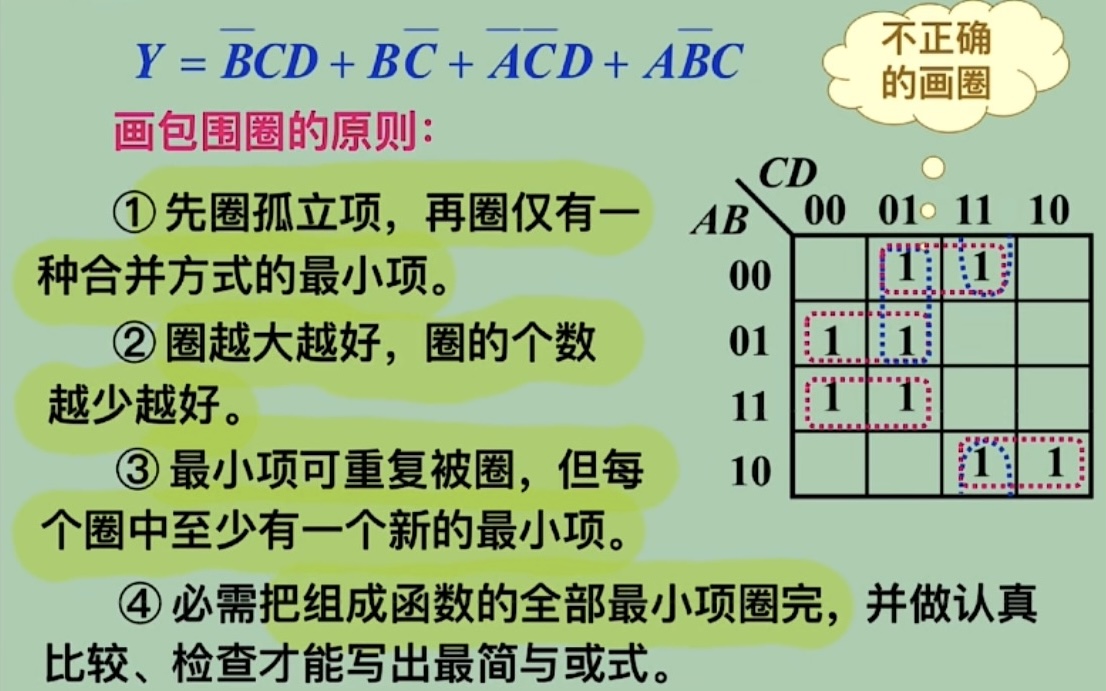
最简与或:包含的乘积项已经最少,每个乘积项的因子也最少,称为最简的与 - 或逻辑式
