信号分析与处理 ¶

约 5637 个字预计阅读时间 22 分钟

课程信息

回忆卷资源

23-24 回忆卷
 课件例题
 2022-2023 春夏《信号分析与处理》回忆卷
 2023电气学院信号分析与处理回忆卷
 信号分析与处理（控院电院）2022春夏回忆卷
 2022春夏信号分析与处理部分回忆卷及复习建议
 《信号分析与处理》2020-2021春夏期末回忆卷及复习整理

《信号分析与处理》课件例题整理
 梁毅浩学长资料
 张建老师ppt
赵光宙习题答案
 赵光宙第二版答案
 信号分析与处理郑军老师实验指导书

经验教训总结 ¶

这门课其实在考试周之前是几乎没有学过的，信号作业两周才布置一次，我前一周没有听懂的东西，后续也没有跟进对齐，就越落越多了。后面几次作业也都是随便写写交了。最后所以最后期末花了比较久的时间时间补天。

期中左右开始就开始听不懂且落课了，尤其是几种变换都讲完以后，学过的东西都糊在了一起。最后只在信号处理部分（比较独立的部分）才跟着课堂听课。

所以这篇内容应该比较适合期末补天时间不是特别紧张的同学。

我的复习顺序是( 仅供参考 )

（大概一天） - 先从比较独立的部分开始：滤波器部分直接听老师上课讲，非常清楚，看完之后把课件例题和课本例题做掉。这部分重点掌握一下：几种设计方法的优缺点（可能会考简答）。巴特沃斯的设计方法：归一化、阶数$n$的计算，反归一化等。 - 系统分析和信号处理部分其实可以放在第二个复习。大部分是自控或是常微分的内容，这部分题型也比较固定，掌握课本课件的例题其实就差不多了。重点关注一下z变换（正反）是怎么变，收敛域问题。

（1-2 天） - 自己看书看到DFT之前，重点理解傅里叶变换的各种性质、连续周期函数的傅里叶变换（下面笔记中列了）、时频域采样定理（非常非常重要）、从正交分解的角度理解各个变换 - DFT和FFT部分可以找几个b站视频看一下速成一下，先明白怎么使用，再看zj的智云

（剩余的时间） - 听一下zj的复习课，串讲一下几种变换以及其他内容。做一下课件例题 - 这个时候就可以开始做历年卷了。做1-2套其实时间就应该到考试前一天or半天了，到这个程度应该通过考试就差不多了。尽量做到每一个题都搞清楚是怎么变化的。整理一下对应的考点和注意事项。

张健老师的课讲的还是很清楚的，但比较可惜的是，我跟上进度的时候课程已经结课了

其实比较建议的是期中之前自己看书学的，信号课本写的还是比较清楚的，要是上课听不懂的话，建议自己看课本学习（不要背诵公式）。但是根据经验来说，~~一般不到最后是没有这个觉悟的~~

用到的一些资料

资料链接

资料目录

│  信号分析处理.xmind
│
├─作业
│      3-FFT作业.pdf
│      4-信号处理基础作业.pdf
│      5-滤波器作业.pdf
│      赵光宙第二版答案.pdf
│
├─实验
│      上机实验一_离散傅里叶变换.pdf
│      信号与处理实验-matlab实验.pdf
│      实物实验2 幅度调制与解调-2024-04.pdf
│      实验1 信号的采样与恢复.doc
│      实验2 DFT和FFT.doc
│      实验3 离散时间信号和系统分析.doc
│      实验4 有源滤波器.doc
│
├─整理
│      公式整理.docx
│      复习提纲.pdf
│      复习笔记.pdf
│      常用公式.pdf
│
├─试卷
│      (试卷1)信号分析与处理试卷.pdf
│      (试卷1答案)信号分析与处理试卷(1).pdf
│      (试卷2)信号分析与处理试卷.pdf
│      (试卷2答案)信号分析与处理试卷(1).pdf
│      (试卷3)信号分析与处理试卷.pdf
│      (试卷3答案)信号分析与处理试卷(1).pdf
│      2022-2023 春夏《信号分析与处理》回忆卷.pdf
│      课件例题.pdf
│
└─课件
        信号与系统(郑君里第二版).pdf
        张健复习ppt.pdf
        第1章 - 绪论.pdf
        第2章－1（时域分析）.pdf
        第2章－2（频域分析）.pdf
        第2章－3（傅立叶变换性质）.pdf
        第3章 离散信号的分析.pdf
        第3章-DFT&FFT.pdf
        第3章－2（频域分析）.pdf
        第3章－3 FFT 20240506.pdf
        第3章－3（DFT、FFT） (2).pdf
        第3章－4-Z变换.pdf
        第4章-信号处理基础.pdf
        第5章－1模拟滤波器.pdf
        第5章－2数字滤波器.pdf

（如果之后可以希望可以增加一下对应的题目练习和反馈，信号没有答案和反馈写作业真的没有什么动力，如果可以的话其实可以一周布置 1-2 个题，就算是课件相似的题也行啊反向督促我这种平时摆烂的人每周都复习一下。有同学提到按照标准过程写的作业仍然会有扣分，这部分可能和不同助教有关系，不太懂。）

信号分类 + 连续信号分析 ¶

连续信号

模拟信号和数字信号的定义

模拟：时间幅度均连续

离散：时间幅度均离散

幅度信号和功率信号

幅度有限的周期信号必定是功率信号正确

信号的变换

要注意所有变换都是针对自变量而言的。要注意正负号的问题

采用正交分解的视角观察 补充知识：正交基下的坐标求解，复向量的内积求法。

推荐几篇写的很好的博客 CFS , CTFT , DFS

Bug

写出非周期连续信号傅里叶变换和周期连续信号傅里叶变换的公式，并简述他们的特点。

傅里叶变换的各种性质¶

比较重要，需要反复记忆背诵

Bug

$\mathscr{F}(Sa(\frac{t}{2})) = ?\quad \int_{-\infty}^{\infty}Sa(\frac{t}{2})dt = ?$ 解答：
第一问使用 CFT 的尺度变换性质
第二问其实是一类题目，通常都是常见变换中少了一项，少了 $\frac{1}{2\pi} (, 或是少了 \(e^{j \omega t}$( 找到缺失的 \)\omega\) 或者 $t$). 这种题目就是找到等价的时域值或者是频域值就行了。今年考试中有多个题目都运用了这种思想。

连续信号的傅里叶变换频谱是双边谱

错误，实连续信号可以；但复指数信号不行例如$e^{j\omega_0 t} \rightarrow 2\pi \delta(\omega-\omega_0)$

各种常见信号傅里叶变换需要记住 - $cos(\omega_0 t)$频谱搬移 - 门函数的表达 $u(t) - u(t-t_0)$

微分性质

最保险的方法是把原函数的解析表达式写出来然后一步一步求微分

需要注意直流分量的处理 : 如果有直流分量，那么只能使用积分变换解决

例题

\[ y(t) = t(u(t)-u(t-1)) \]

因为 $tu(t)=0$,$tu(t-1)$ 只能在 $t=1$ 处取值

\[ \begin{align*} y'(t) &= (u(t)-u(t-1)) + t(\delta(t)-\delta(t-1))\\ &= u(t)-u(t-1) - \delta(t-1) \end{align*} \]

对称性

\[ x^*(t) \stackrel{\mathscr{F}}{\longrightarrow}X^*(-\omega) \]

对偶性

单位冲激信号和直流

采样信号和门函数

帕斯瓦尔定理

从时域和频域分别表述信号的能量

n 维空间的勾股定理可以看这篇回答

周期信号的傅里叶变换（!! 非常重要）¶

周期信号可以表示为

\[ \begin{align} x(t) &= \mathop{\Sigma}\limits_{n=-\infty}^{\infty}X(n\omega_0)e^{jn\omega_0t}\\ X(\omega) &= \mathscr{F}(\mathop{\Sigma}\limits_{n=-\infty}^{\infty}X(n\omega_0)e^{jn\omega_0t})\\ &= X(n\omega_0)\mathscr{F}(e^{jn\omega_0t})\\ &=X(n\omega_0)\mathop{\Sigma}\limits_{n=-\infty}^{\infty} 2\pi \delta(\omega - n \omega_0) \end{align} \]

例子 : 求周期为 $T_0$ 的周期性冲激串 $\delta_T(t)$ 的傅里叶变换。

课本 P42,P43

\[ \begin{align*} \delta_T(t)&= \mathop{\sum}\limits_{n=-\infty}^{\infty}\delta(t-nT_0)\\ \delta_T(t)&= \mathop{\sum}\limits_{n=-\infty}^{\infty}X(n\omega_0)e^{jn\omega_0t} \end{align*} \]

又因为在一个周期内 $X(n\omega_0) = \frac{1}{T_0} \int^\frac{T_0}{2}_{-\frac{T_0}{2}} \delta_T(t)e^{-jn\omega_0 t} = \frac{1}{T_0}$ 所以可以求得

\[ \begin{align*} X(\omega) = \mathop{\sum}\limits_{n=-\infty}^{\infty} 2\pi \frac{1}{T_0} \delta(\omega-n \omega_0) = \omega_0 \mathop{\sum}\limits_{n=-\infty}^{\infty}{\delta(\omega-n \omega_0) } \end{align*} \]

该式子在推导时域、频域采样定理时候反复出现

离散信号的分析 ¶

离散信号

常见离散信号、信号的时域计算 关于信号卷积、相关性和反卷积，可以看这一篇

相关可以看作是向量内积的推广（内积为两向量点乘，其物理意义为将一个向量投影到另一个向量）：

\[ <\vec{a},\vec{b}> = \vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cos \theta \]

内积越大，投影越大，两个向量间夹角越小，方向越一致，相似度越高。特别地，当内积为 0 时，两个向量是垂直的；只有当两个向量夹角为 0 时，内积最大（相关系数也最大）。因此，相关可反映两个向量空间的夹角。

时频域采样定理 (!!! 很重要 ) ¶

时域采样 , 采样间隔 $T_s$ - 频谱发生周期延拓，延拓周期是$\omega_s$ - 频谱乘以$\frac{1}{T_s}$

例题

取样函数（内插函数）加权求和构成的无穷级数；将抽样信号通过一个理想低通滤波器。

频域采样，频率间隔 $\omega_s$ - 时域周期$T_s$进行延拓 - 幅度乘以$\frac{1}{\omega_s}$

卷积的计算方法¶

对位相乘求和

归一化角频率(!! 一定要搞明白 ) ¶

$\Omega$ 的单位是弧度，表示的是一个采样周期内转过的角度，自然而然可以得出计算公式

\[ \Omega = \omega_0 T_s = \frac{2\pi}{T_0}T_s = \frac{2\pi}{N T_s}T_s = \frac{2\pi}{N} \]

其中，$\Omega$ 是数字角频率，$T_s,w_s$ 是采样，$\omega_0$ 是模拟角频率，$N$ 采样点数

采样时长 $T = N\cdot T_s$
模拟角频率 $\omega_0 = \frac{2\pi}{T_0} = 2\pi f_0$
实际频率 $f = \frac{f_s}{N} \cdot K$

原因：我们拿到一串数字信号，不可能还附带着把采样间隔也告诉你。或者说，信号就是信号，在这组关于时间的一维信号上是没有采样率这样的信息的。有一个大聪明发现，反正经过采样后的数字信号在频域上是周期性的，这个周期只与采样率有关，那我想办法忽略采样率，让周期都变成 $2\pi$，岂不是更好，那样很多算法就通用了。所以搞出来一个归一化角频率。

DFS¶

DFS 的推导 课本：利用冲激函数串进行采样，计算傅里叶变换（参考对周期函数进行傅里叶变换的例题）

这篇文章给出了从正交分解的视角看待 DFS。

正交基必须与原向量等维度

内插公式如何理解

DFS 性质

共轭对称性若$x(n) \stackrel{DFS}{\longrightarrow} X(k\Omega_0)$，则有

\[ x^*(-n)\stackrel{DFS}{\rightleftharpoons} X^*(k\Omega_0) \]

DFT¶

公式中各个字母的含义

\[ X(l) = \sum^{N-1}_{k=0} x(k)W_M^{kl} = \sum^{N-1}_{k=0} x(k)e^{-j\frac{2\pi}{M}kl} \]

$l$：频谱采样的序号 , 频域采样第几个点
$k$: 时域序列点的序号
$N$: 时域内截取数据的长度
$M$: 频域点的个数

频域采样 $N$ 点，时域延拓的周期也是 N 点，每两个点的间隔为采样周期 $T_s$，所以周期延拓的周期是 $N\cdot T_s$

圆周移位

比较重要

\[ x((n-m))_NR_N(n) \stackrel{DFT}{\rightarrow} X(k) e^{-j k \frac{2\pi}{N}m} \]

题目

DFT-question

实数序列，根据共轭对称性 ,$X(k) = X^*(N-k)$ answer

计算量

每计算一个 $X(k)$ 值需要进行 $N$ 次复数相乘，$N-1$ 次复数相加 ;

对于 $N$ 个 $X(k) $ 点完成全部 DFT 运算共需

$N^2$ 次复数相乘和 $N(N-1)$ 次复数加法。
$4N^2$ 次实数乘法 ,$2N^2 +2N(N-1)\approx 4N^2$ 次实数加法

FFT 算法¶

张健智云 01- 四种变换总结 +FFT 开头

张健智云 02-FFT 计算

张健智云 03-FFT 谱分析误差

基本思想

将原始的 N 点序列，一次分解成一系列短序列，并充分利用 $W_N^{nk}$ 的对称性质和周期性质，求出短序列的 DFT，适当组合后再求出长序列的 DFT，减少乘法运算。

令

\[ W_N = e^{-j\frac{2\pi}{N}} \]

\[ X(k) = G(k) + W_N^{nk} H(k)\\ X(k + \frac{N}{2}) = G(k) - W_N^{nk} H(k) \]

可视化理解 , 前半部分有点冗余

简单理解

复杂度计算，因为 FFT 相当于把规模为 N 的问题，每次拆分成两个规模为 $\frac{N}{2}$ 的问题，然后用 $o(1)$ 的时间进行处理。

由主定理可得（主定理部分内容详见数据结构）

\[ T(n) = aT(\frac{n}{b}) + f(n) \]

$a = 2, b = 2 \therefore T(n) = n\log n$ 是复杂度，不是准确乘加法数值！

FFT 逆变换

两种方法进行求解： * 全系数取反，结果最后乘$\frac{1}{N}$,直接求出来的就是序列 * 因为实数序列共轭是本身，所以先取共轭序列列，再使用蝶形运算，求出来的是序列的共轭，这个时候要再注意一次取反。

\[ \begin{align*} x^*(n) = [ \frac{1}{N} \sum \limits_{n=0}^{N-1}X(k)W_N^{-kn}]^* = \frac{1}{N}DFT[X^*(k)] \end{align*} \]

蝶形运算

N 点序列 FFT 运算

运算次数：复数乘法总数 $\frac{N}{2}\log_2{N}$, 复数加法 $Nlog_2 N $ 对应实数乘法 $2N\log_2{N}$, 实数加法 $3N\log_2{N}$
存储空间：$N + \frac{N}{2}$
全系数：因为想要节省内存空间，所以将中间的系数根据可约性进行统一，统一成 $W_N^{kn}$ 的形式，下标都为 $N$
倒位序：输入自然序，输出倒位序；输入倒位序，输出自然序

计算线性卷积

圆周卷积是线性卷积周期延拓取主值（DFT是DTFT取主值）

先补零，再反转，再卷积。

谱分析

时限连续信号：频域无限长，必定会有混叠；采用抗混叠滤波器去除次要的高频信号，再进行采样；或者选择合适的 $T_s$，减少混叠的影响。
带限连续信号：时宽无限，会出现频谱泄漏；加大时宽 $\tau$ 或者选择形状合适的窗函数；
连续周期信号：时域正周期截断

历年题

是一个频率向数字角频率转换的过程。

FFT 进行计算，先得补零至 $2^{10}=1024$ 个点
$k\cdot \frac{2\pi}{N} = \frac{2\pi f}{f_s} = \Omega$
带入后求解得 $k = 40$, 若求频谱，则求 $X(40)$

其中，频率分辨率 $\Delta f = \frac{f_s}{N}$,$f_s$ 可以算出最高频率，$N$ 可以算出来频谱间距

z 变换¶

张健智云这部分其实直接看书就行了，有联系的是微积分2数列收敛性分析、复变函数洛朗级数、

常用 z 变换 最常用的应该是

\[ a^n u(n) \stackrel{\mathscr{z}}{\rightarrow} \frac{z}{z-a} \]

$cos(\omega_0 n)$ 也是一样的做法，按照欧拉公式对 $\cos (\omega_0 n )= \frac{1}{2}(e^{j\omega_0 n} + e^{-j\omega_0 n})$ 将$e^{j\omega_0}$看作$a$即可

z 变换的定义域问题

z 变换的直观意义

z 变换和复变中的保角映射的联系

单边 z 变换的特殊性质 单边z变换就是加上了因果序列$u(n)$

时移定理

\[ \begin{align*} move \ left :\mathscr{Z}[x(n+m)u(n)] = z^m \left[X(z) - \sum^{m-1}_{k=0}x(k)z^{-k}\right]\\ move \ right :\mathscr{Z}[x(n-m)u(n)] = z^{-m} \left[X(z) - \sum^{-1}_{k=-m}x(k)z^{-k}\right] \end{align*} \]

初值定理 $x(0) = \lim\limits_{z\rightarrow \infty}X(z)$
终值定理 $\lim\limits_{n\rightarrow\infty}x(n) = \lim\limits_{z-\rightarrow 1}[(z-1)X(z)]$

一个很巧妙的题

思路：一开始没有看明白答案在干什么。后来看题才发现，题目中给出了 $y(n)$ 的所有情况，只是没有用分段函数的方法给出而已。知道了这个点之后，这个题就不难了。

\[ \begin{align*} Y(z)&=\sum_{n=-\infty}^{\infty}y(n)z^{-n}\\ &=\sum_{r=-\infty}^{\infty}y(3r)z^{-3r}+\sum_{r=-\infty}^{\infty}y(3r+1)z^{-(3r+1)}+\sum_{r=-\infty}^{\infty}y(3r+2)z^{-(3r+2)}\\ &=\sum_{r=-\infty}^{\infty}x(r)z^{-3r}+\sum_{r=-\infty}^{\infty}0.5x(r)z^{-(3r+1)}\\ &=X(z^3)+0.5z^{-1}X(z^3)\\ &=(1+0.5z^{-1})X(z^3) \end{align*} \]

各种变换之间的关系 ¶

DFT，DFS，DTFT

DFS→DFT：DFT 是 DFS 的主值序列，是一种通过 DFS 得出的变换，将有限非周期离散信号的频谱离散化

DTFT→DFT：DFT 是在主周期 $[-\pi,\pi]$ 上按 $\Omega_0 = \frac{2\pi}{N}$ 为采样间隔进行采样 .

频域采样后时域发生周期延拓，周期为 N

z 变换和其他变换的关系

与傅里叶变换：z 变换是蜡像抽样信号拉普拉斯变换进行 $z = e^{sT_s}$ 映射的结果；有 $X(z) = X_s(s)|_{s = \frac{\ln{z}}{T_s}}$
与 DTFT：DTFT 就是在 z 平面单位圆上的 z 变换。可以先求出 z 变换，再用 $z=e^{j\Omega}$ 替换
与 DFT：DFT 视为序列的 z 变换在单位圆上取样间隔 $\Omega_0 = \frac{2\pi}{N}$ 的均匀取样

共轭对称性 ¶

这一块没搞懂，但是考试没有涉及，历年题考查的也不多。

共轭对称讲解

共轭对称性讲解视频，还挺清楚的

复序列的对称性

若 $x(n)$ 为复序列

共轭对称序列(Conjugate-Symmetry Sequence)：实部为偶对称，虚部为奇对称，即表示为

\[ x_{e}(n)=x_{e}^{*}(-n) \]

例如：

\[ x(n) = [1,j,-1,-j] \]

共轭反对称序列( Conjugate-Antisymmetry Sequence): 满足其实部为奇对称，虚部为偶对称，即表示为

\[ x_{o}(n)=-x_{o}^{*}(-n) \]

例如

\[ x(n) = [0,j,0,j] \]

任何复序列都可以被分解为一个共轭对称序列和一个共轭反对称序列之和。即

\[ x(n)=x_{e}(n)+x_{o}(n) \]

其中

\[ \begin{align*} x_{e}(n)=\frac{1}{2}\left[x(n)+x^{*}(-n)\right]\\ x_{0}(n)=\frac{1}{2}\left[x(n)-x^{*}(-n)\right] \end{align*} \]

实偶序列的傅里叶变换是实偶函数，实奇序列的傅里叶变换是纯需奇函数

傅里叶变换

\[ X(j \omega)=X_e(j \omega)+X_o(j \omega) \]

其中

\[ X_e(j \omega)=\frac{1}{2}\left[X(j \omega)+X^{*}(-j \omega)\right] \]

\[ X_o(j \omega)=\frac{1}{2}\left[X(j \omega)-X^{*}(-j \omega)\right] \]

序列的实部和虚部与其傅里叶变换的共轭对称部分和共轭反对称部分存在如下关系：

若 $\mathrm{FT}\{x(n)\}=X(j \omega)$，则

\[ \mathrm{FT}\{\operatorname{Re}[x(n)]\}=X_e(j \omega) \]

\[ \mathrm{FT}\{\operatorname{Im}[x(n)]\}=X_o(j \omega) \]

序列的共轭对称部分与共轭反对称部分的傅里叶变换

任一序列 $x(n)$ 的共轭对称部分 $x_c(n)$ 的傅里叶变换，为 $x(n)$ 的傅里叶变换 $X(j \omega)$ 的实部，其共轭反对称部分 $x_a(n)$ 的傅里叶变换为 $X(j \omega)$ 的虚部。即

\[ \mathrm{FT}\left[x_e(n)\right]=\operatorname{Re}[X(j \omega)] \]

\[ \mathrm{FT}\left[x_o(n)\right]=\operatorname{Im}[X(j \omega)] \]

离散 x共轭 - X先共轭再翻转

x 反转再共轭 - X 共轭

对于实数序列，就有 $X(k) = X^*(n-k)$

信号处理 ¶

系统类型 ¶

时变非时变

注意所有操作都是对 $t$ 进行，不要想当然；

证明顺序 $y_1(t)$,$x_2(t) = x_1(t-t_0)$, 求 $y_2(t)$

只对 t 进行操作，不是对括号内所有的进行变换

比如下面的信号

\[ y(t) = x(-t) \]

\[ 证:\quad \begin{align*} y_1(t) &= x_1(-t) \\ y_1(t-t_0) &= x_1(-t+t_0)\\ x_2 &= x_1(t-t_0)\\ y_2(t) &= x_2(-t) = x_1(-t-t_0) \end{align*}\\ 只对t进行操作 \]

系统部分¶

s 域

\[ \mathscr{L}[y^{(i)}(t)] = s^i Y(s)-\sum_{k=0}^{i-1}s^{s-i-k}y^{(k)}(0-) \]

\[ \mathscr{y''} = s^2Y(s) - sy(0-) - y'(0)\\ \mathscr{y'} = sY(s) - y(0-) \]

z 域

零状态响应：系统没有内部条件

零输入响应：输入为 0 时候的响应

\[ y(t) = y_{zs}(t)+y_{zi}(t)\\ y(n) = y_{zs}(n) + y_{zi}(n) \]

时域

\[ \sum_{k=0}^{n}a_k y^{(k)}(t) = \sum^{m}_{k=0}b_kx^{(k)}(t) \]

单位冲激响应：

n>m （物理可实现）$h(t) = \sum^{n}_{i=1} A_i e^{\lambda_i t}u(t)$
n=m: $h(t) = c\delta(t) + \sum^{n}_{i=1} A_i e^{\lambda_i t}u(t)$
n<m: $h(t) = \sum_{j=0}^{m-n}c_j \delta^{(j)}(t) + \sum^{n}_{i=1} A_i e^{\lambda_i t}u(t)$

\[ \sum_{k=0}^{N}a_k y(n-k) = \sum^{M}_{k=0}b_kx(n-k) \]

单位脉冲响应：

$N>M$:$\sum_{i=1}^{N}A_i\lambda_i^n u(n)$
$N\le M$: $h(n) = \sum^{N-M}_{j=0} C_j \delta(n-j) + \sum^{N}_{i=1}A_i\lambda_i^Nu(n)$

时域分析¶

知道单位冲激响应之后，就可以计算零状态响应了

\[ y(t) = x(t) * h(t) \]

$t<0$ 时候，$x(t) = 0$，所以积分下限取 0
$\tau> t$ 时候，$t-\tau <0$ ，$h(t-\tau)=0$ 积分上限取 $t$

$\int_{-\infty}^{t}\delta(\tau)d\tau = u(t)$

无失真传输¶

通过传输系统，波形不变，幅度可以放缩，允许时延

\[ y(t) = kx(t-t_0)\\ Y(\omega) = Ke^{-j\omega t_0}\\ \]

\[ |H(\omega) |= K\\ \phi_n(\omega) = -\omega t_0 \]

判断稳定性¶

单位圆内没有极点

当 $H(z)$ 的极点全部位于 z 平面单位圆内部的时候，系统稳定

这个时候才可以用初值定理和终值定理

稳态响应¶

先求频率特性函数

离散系统的频率特性函数 $H(\Omega)$ 可以由 $H(z)$ 求取

\[ H(\Omega) = H(z)|_{z = e^{j\Omega}} \]

再带入对应的 $\Omega$

滤波器 ¶

模拟滤波器

数字滤波器

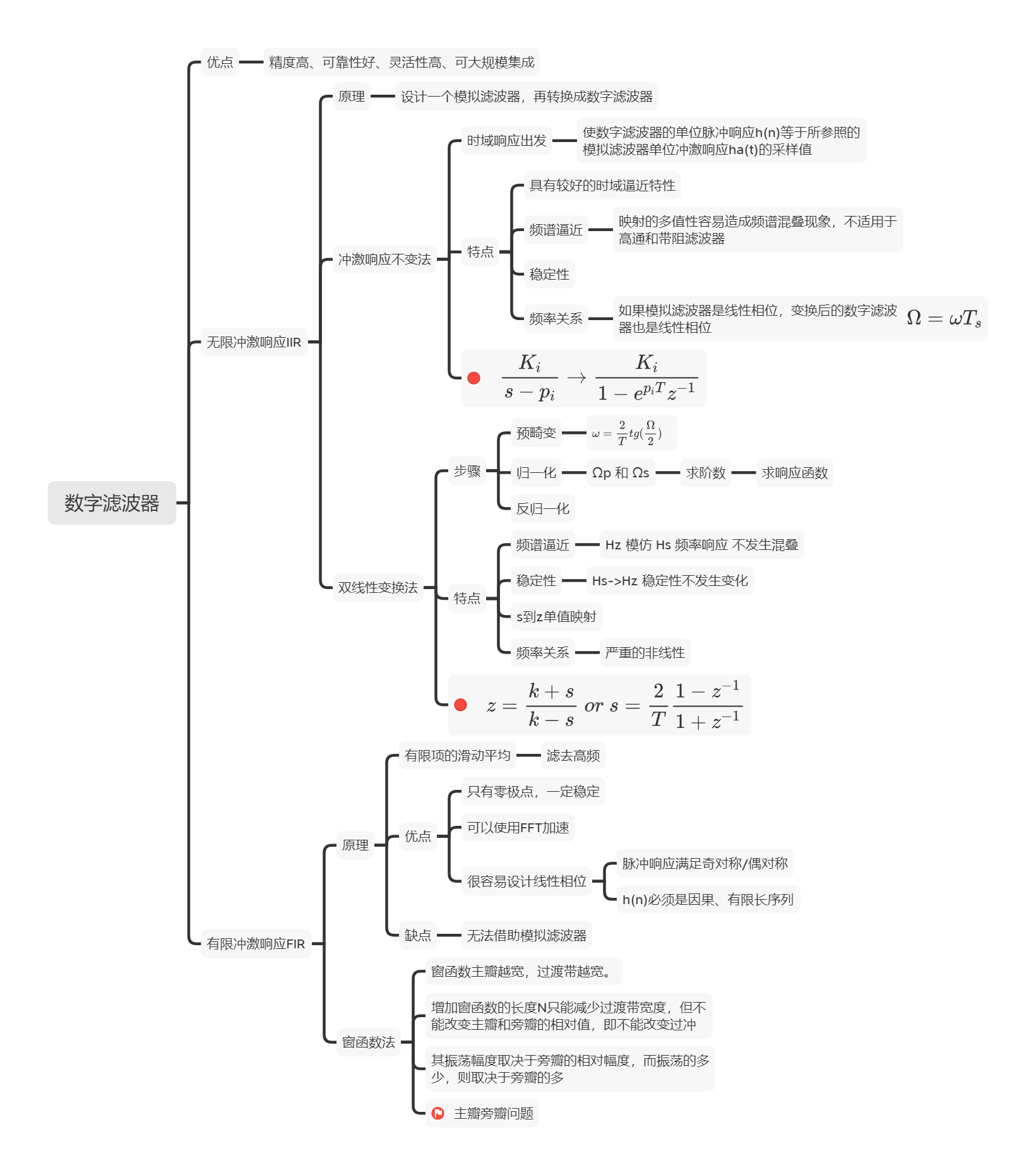
冲激响应不变法

由数字角频率向模拟角频率变换的过程中，频率对应关系是

s 域到 z 域的映射是多值映射，在高频部分会出现混叠。

双线性法 把整个平面压缩到$[-\frac{\pi}{T_s} ~ \frac{\pi}{T_s}]$区间 s域到z域单值映射，不会出现混叠

经过非线性畸变

\[ z = \frac{k+s}{k-s}\\ s = \frac{2}{T}\frac{1+z^-1}{1-z^{-1}} \]

FIR 滤波器

窗函数设计 FIR

主瓣、旁瓣、过冲值分别代指哪个部分