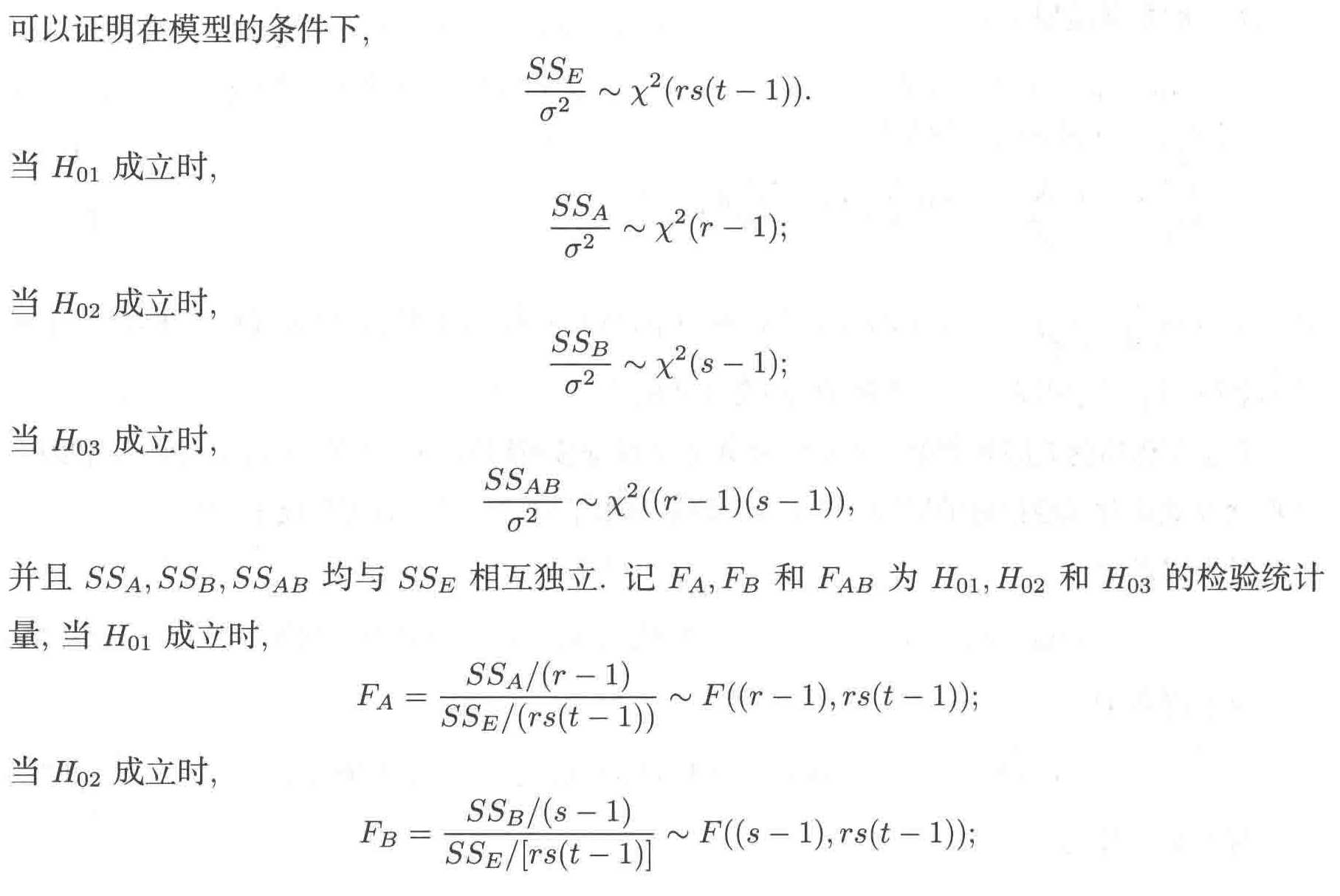方差分析 | ANOVA ¶

约 1298 个字 25 行代码预计阅读时间 5 分钟

anova 是 analysis of variance 的缩写，中文译为方差分析。

由英国统计学家罗纳德 · 费舍尔（Ronald A. Fisher）提出，用于推断两个以上总体均值是否有差异的显著性检验

前提 ¶

单因素 ¶

因素 (factor): 对实验指标产生影响
水平 (level): 因素中各个不同状态

方差分析 ¶

方差分析就是要比较因素 \(A\) 的 \(r\) 个水平下试验指标理论均值的差异，问题可归结为比较这 \(r\) 个总体的均值差异，即检验假设：

\[ H_0: \mu_1 = \mu_2 = \ldots = \mu_r, \quad H_1: \mu_1, \mu_2, \ldots, \mu_r \text{不全相等}. \]

其中 \(\mu = \frac{1}{n} \sum_{i=1}^{r} n_i \mu_i\) 称为总平均；

如果 \(H_0\) 被拒绝，则说明因素 A 的各水平的效应之间有显著的差异，即认为因素 A 的变化对试验指标有影响；否则，认为因素 A 的变化对试验指标并没有影响，数据的差异来自随机误差。

平方和分解 ¶

检验假设的检验统计量是在平方和分解的基础上导出的。

\[ SS_T = \sum_{i=1}^{r} \sum_{j=1}^{n_i} (X_{ij} - \bar{X})^2, \quad \bar{X} = \frac{1}{n} \sum_{i=1}^{r} \sum_{j=1}^{n_i} X_{ij}, \quad \bar{X}_i. = \frac{1}{n_i} \sum_{j=1}^{n_i} X_{ij} \]

平方和分解的主要思想是把数据总的差异（用总离差平方和（total sum of squares）\(SST\)

一部分是由于因素 A 引起的变异，即效应平方和 \(SSA\)：

\[ SS_A = \sum_{i=1}^{r} \sum_{j=1}^{n_i} (\bar{X}_i. - \bar{X})^2 = \sum_{i=1}^{r} n_i (\bar{X}_i. - \bar{X})^2 \]

另一部分则是由随机误差所引起的变异，即误差平方和（error sum of squares）\(SS_E\)：

\[ SS_E = \sum_{i=1}^{r} \sum_{j=1}^{n_i} (X_{ij} - \bar{X}_i.)^2 \]

经计算可以得到平方和分解公式：

\[ SS_T = SS_E + SS_A. \]

性质 ¶

\(\frac{SSE}{\sigma^2} \sim \chi^2(n-r)\)；
\(SS_E\) 和 \(SS_A\) 相互独立；
\(E(SS_A) = (r-1)\sigma^2 + \sum_{i=1}^{r} n_i \alpha_i^2\)，进一步，在假设 \(H_0\) 为真时，\(\frac{SS_A}{\sigma^2} \sim \chi^2(r-1)\)。

因此，在假设 \(H_0\) 为真时，

\[ F = \frac{MS_A}{MS_E} \sim F(r-1, n-r). \]

其中 \(MSA = \frac{SSA}{r-1}, MSE = \frac{SSE}{n-r}\)。

从定理 9.1.1 可以看出，无论假设 \(H_0\) 是不是真，\(E[SSE/\sigma^2(n-r)] = 1\)。而对于 \(SSA\)，只有当假设 \(H_0\) 为真的时候 \(E[SSA/\sigma^2(r-1)] = 1\)。如果假设 \(H_0\) 不真，则 \(E[SSA/\sigma^2(r-1)] > 1\)，因此，如果由样本计算得出的 F 值比较大的话，即落在 \(\{F \geq c\}\) 的区间内，那么判定假设 \(H_0\) 不成立。

对于给定的显著水平 \(\alpha\)，用 \(F_{\alpha}(r-1, n-r)\) 表示 F 分布的上侧 \(\alpha\) 分位数，这个假设检验的拒绝域为 \(W = \{F \geq F_{\alpha}(r-1, n-r)\}\)。即当由观察值得到的 F 值落在拒绝域内，则意味着应该拒绝原假设 \(H_0\)，认为各总体均值（各个水平下）有差异，即因素 A 显著。或计算 \(P = P\{F(r-1, n-r) \geq F\}\)，当 \(P \leq \alpha\) 时拒绝原假设 \(H_0\)。通常将上述的计算归纳成表 9.1.3，称为方差分析表（analysis of variance table）。

\(\sigma^2\) 的无偏估计 ¶

\[ MS_E = \frac{SS_E}{n-r} = \frac{1}{n-r}\sum_{i=1}^r\sum_{j=1}^{n_i}(X_{ij}-\bar{X_i})^2 \]

判断方法 ¶

(1) 根据前面所给出的 F 检验查出 \(F_{\alpha}(r-1, n-r)\) 的值，给出拒绝域 \(W = \{F \geq F_{\alpha}(r-1, n-r)\}\)，根据 F 是否落入拒绝域中

(2) 根据 p 值。如果 P 值小于等于给定的显著水平，那么拒绝假设 \(H_0\)。

t 检验均值

x=[2.74,2.75,2.72,2.69]
y=[2.75,2.78,2.74,2.76,2.72]
print(st.ttest_ind(x,y))

计算

meanx=np.mean(x)
meany=np.mean(y)
meanall=np.float64(sum(x+y)/len(x+y))

ssa=len(x)*((meanx-meanall)**2)+len(y)*((meany-meanall)**2)
sse = sum((x-meanx)**2)+sum((y-meany)**2)
sta=ssa/(sse/(len(x)+len(y)-2))
print(sta,1-st.f(1,len(x)+len(y)-2).cdf(sta))
print(st.f_oneway(x,y))
print(st.ttest_ind(x,y))

无相互影响多因素 ¶

双因素方差分析与单因素方差分析的基本原理相同，基于平方和的分解，总的平方和 \(SS_T\) 可以分解为因素 A 不同水平所引起的离差平方和 \(SS_A\)，因素 B 不同水平所引起的离差平方和 \(SS_B\)，以及由随机误差引起的误差平方和 \(SS_E\)。即

\[ SST = SSA + SSB + SSE, \]

其中

\[ \begin{aligned} SST &= \sum_{i=1}^{r} \sum_{j=1}^{s} (X_{ij} - \bar{X})^2, \quad \bar{X} = \frac{1}{rs} \sum_{i=1}^{r} \sum_{j=1}^{s} X_{ij}, \\ SSA &= \sum_{i=1}^{r} s (\bar{X}_{i.} - \bar{X})^2, \quad \bar{X}_i = \frac{1}{s} \sum_{j=1}^{s} X_{ij}, \\ SSB &= \sum_{j=1}^{s} r (\bar{X}_{.j} - \bar{X})^2, \quad \bar{X}_j = \frac{1}{r} \sum_{i=1}^{r} X_{ij}, \\ SSE &= \sum_{i=1}^{r} \sum_{j=1}^{s} (X_{ij} - \bar{X}_{i.} - \bar{X}_{.j} + \bar{X})^2. \end{aligned} \]

性质 ¶

\[ \frac{SS_E}{\sigma^2} \sim \chi^2((r-1)(s-1)), \]

当 \(H_{01}\) 成立时，

\[ \frac{SS_A}{\sigma^2} \sim \chi^2(r-1), \]

当 \(H_{02}\) 成立时，

\[ \frac{SS_B}{\sigma^2} \sim \chi^2(s-1). \]

并且 \(SSA, SSB\) 和 \(SSE\) 相互独立。记 \(FA\) 和 \(FB\) 为 \(H_{01}\) 和 \(H_{02}\) 的检验统计量，当 \(H_{01}\) 成立时，

\[ F_A = \frac{SS_A/(r-1)}{SS_E/[(r-1)(s-1)]} \sim F(r-1, (r-1)(s-1)); \]

当 \(H_{02}\) 成立时，

\[ FB = \frac{SSB/(s-1)}{SSE/[(r-1)(s-1)]} \sim F((s-1), (r-1)(s-1)). \]

检验拒绝域分别为

\[ \begin{aligned} W_A &= \{FA \geq F_{\alpha}((r-1), (r-1)(s-1))\}, \\ W_B &= \{FB \geq F_{\alpha}((s-1), (r-1)(s-1))\}. \end{aligned} \]

由观测样本计算得到 \(FA\) 和 \(FB\) 的值，根据这些值是否落在拒绝域内，判断是拒绝还是接受 \(H_{01}\) 和 \(H_{02}\)。计算结果可归纳成下面的方差分析表

无影响多因素使用 ols&anova_lm

from statsmodels.stats.anova import anova_lm
from statsmodels.formula.api import ols

model = ols('S ~ C(E)+C(M)', data=salary_table).fit()
table1 = anova_lm(model)
print(table1)
table2 = anova_lm(model,typ=2) # 计算A因素的时候，B因素的计算方式有不同
print(table2)

根据结果判断

            df        sum_sq       mean_sq          F        PR(>F)
C(E)       2.0  1.091346e+08  5.456732e+07   6.009323  5.067776e-03
C(M)       1.0  5.105843e+08  5.105843e+08  56.229001  2.837753e-09
Residual  42.0  3.813786e+08  9.080444e+06        NaN           NaN

方差分析 | ANOVA ¶

前提 ¶

单因素 ¶

方差分析 ¶

平方和分解 ¶

性质 ¶

\(\sigma^2\) 的无偏估计 ¶

判断方法 ¶

无相互影响多因素 ¶

性质 ¶

有相互影响的多因素 ¶