假设检验 ¶

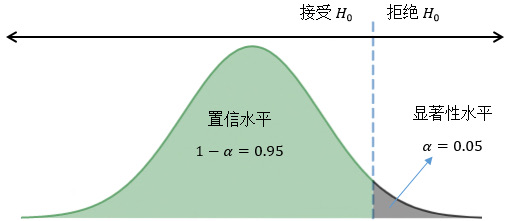
把公认成立的结论作为 $H_0$, 把想要验证的结论作为 $H_1$；目的是排除随机涨落的影响，证明颠覆性的结论、、

表达式的具体形式不重要，不管分子分母，重要的是表达式本身服从的分布和置信区间怎么取

一般的流程： 假设真理→计算真理条件下容许出错的样本空间→落在这个之外的就拒绝

检验错误 ¶

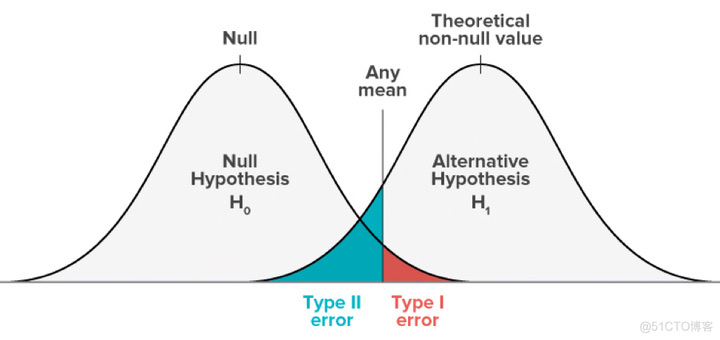
	拒绝假设	接受假设
$H_0$ 正确	Type Ⅰ error $\alpha$	$1-\alpha$
$H_1$ 正确	$1-\beta$	Type Ⅱ error $\beta$

一类错误和二类错误无法同时变小
通常要求一类错误的概率小

不要老关注平均值，误差才是重要的

In [1]:

Copied!





import numpy as np
import scipy.stats as st
import matplotlib.pyplot as plt

x=np.linspace(-8,8,200)
pdfa=st.norm.pdf(x,-2,1.5)
pdfb=st.norm.pdf(x,1,1.5)
plt.plot(x,pdfa,x,pdfb)
### 一类错误, 功效函数beta
plt.fill_between(x,pdfa,where=x>=0,alpha=0.3)
### 二类错误, 1-beta
plt.fill_between(x,pdfb,where=x<=0,alpha=0.3)
### 两类错误同时变小不可兼得
import numpy as np
import scipy.stats as st
import matplotlib.pyplot as plt

x=np.linspace(-8,8,200)
pdfa=st.norm.pdf(x,-2,1.5)
pdfb=st.norm.pdf(x,1,1.5)
plt.plot(x,pdfa,x,pdfb)
### 一类错误, 功效函数beta
plt.fill_between(x,pdfa,where=x>=0,alpha=0.3)
### 二类错误, 1-beta
plt.fill_between(x,pdfb,where=x<=0,alpha=0.3)
### 两类错误同时变小不可兼得

Out[1]:

<matplotlib.collections.PolyCollection at 0x7f7397b23fe0>

No description has been provided for this image

重要参数检验 ¶

$H_0: \theta \geq \theta_0, H_1: \theta < \theta_0$
$H_0: \theta \leq \theta_0, H_1: \theta > \theta_0$
$H_0: \theta = \theta_0, H_1: \theta \neq \theta_0$

$\theta > \theta_0, \sigma^2$ 已知的检验 ¶

对于任意 $\theta$，根据中心极限定理， $(\bar{\theta}-\theta)/(\sigma/\sqrt{n})$为$N(0,1)$的正态分布

$$ P_{\theta_0}(\bar{\theta} \leq C) = \alpha\\ \Phi((C-\theta_0)/(\sigma/\sqrt{n}))=\alpha\\ C=\theta_0-1.64\sigma/\sqrt{n}, where \ \alpha = 0.05 $$

In [2]:

Copied!





x=np.linspace(-6,6,200)
pdfa=st.norm.pdf(x,-1,1)
pdfb=st.norm.pdf(x,0,1)
pdfc=st.norm.pdf(x,1,1)

plt.plot(x,pdfa,x,pdfb,x,pdfc)

print(st.norm.ppf(0.05))

#画出一类错误
plt.fill_between(x,pdfc,where=x<-1.64,alpha=0.3)
plt.fill_between(x,pdfb,where=x<-1.64,alpha=0.3)
x=np.linspace(-6,6,200)
pdfa=st.norm.pdf(x,-1,1)
pdfb=st.norm.pdf(x,0,1)
pdfc=st.norm.pdf(x,1,1)

plt.plot(x,pdfa,x,pdfb,x,pdfc)

print(st.norm.ppf(0.05))

#画出一类错误
plt.fill_between(x,pdfc,where=x<-1.64,alpha=0.3)
plt.fill_between(x,pdfb,where=x<-1.64,alpha=0.3)

-1.6448536269514729

Out[2]:

<matplotlib.collections.PolyCollection at 0x7f739785c680>

$\theta \leq \theta_0, \sigma^2$ 已知的检验 ¶

$$ C=\theta_0+1.64\sigma/\sqrt{n} $$

In [3]:

Copied!





x=np.linspace(-6,6,200)
pdfa=st.norm.pdf(x,-1,1)
pdfb=st.norm.pdf(x,0,1)
pdfc=st.norm.pdf(x,1,1)

plt.plot(x,pdfa,x,pdfb,x,pdfc)

print(st.norm.ppf(0.95))

plt.fill_between(x,pdfa,where=x>1.64,alpha=0.3)
plt.fill_between(x,pdfb,where=x>1.64,alpha=0.3)
x=np.linspace(-6,6,200)
pdfa=st.norm.pdf(x,-1,1)
pdfb=st.norm.pdf(x,0,1)
pdfc=st.norm.pdf(x,1,1)

plt.plot(x,pdfa,x,pdfb,x,pdfc)

print(st.norm.ppf(0.95))

plt.fill_between(x,pdfa,where=x>1.64,alpha=0.3)
plt.fill_between(x,pdfb,where=x>1.64,alpha=0.3)

1.6448536269514722

Out[3]:

<matplotlib.collections.PolyCollection at 0x7f73976a7b90>

假设检验的矛盾 ¶

当 $\theta_0-1.64\sigma/\sqrt{n} \leq \bar{\theta} \leq \theta_0+1.64\sigma/\sqrt{n}$ 时候，两个假设都成立

$\theta \ge \theta_0$
$\theta \le \theta_0$

$\theta = \theta_0, \sigma^2$ 已知的检验 ¶

$|\bar{\theta} - \theta_0|\leq C$

In [4]:

Copied!

x=np.linspace(-6,6,200)
pdfb=st.norm.pdf(x,0,1)
plt.plot(x,pdfb)

print(st.norm.ppf(0.025))

plt.fill_between(x,pdfb,where=(x>1.96)|(x<-1.96),alpha=0.3)
x=np.linspace(-6,6,200)
pdfb=st.norm.pdf(x,0,1)
plt.plot(x,pdfb)

print(st.norm.ppf(0.025))

plt.fill_between(x,pdfb,where=(x>1.96)|(x<-1.96),alpha=0.3)

-1.9599639845400545

Out[4]:

<matplotlib.collections.PolyCollection at 0x7f73977469c0>

$\sigma$ 未知 ¶

假设检验的三种情况

$H_0 : \theta \geq \theta_0$，$H_1 : \theta < \theta_0$
$H_0 : \theta \leq \theta_0 $,$H_1 : \theta > \theta_0$
$H_0 : \theta = \theta_0$，$H_1 : \theta \neq \theta_0$

$\frac{\bar{\theta} - \theta_0}{S/\sqrt{n}}$ 会近似服从 $t_{n-1}$ 分布。

左侧检验：$\frac{\bar{\theta} - \theta_0}{S/\sqrt{n}} \geq -t_{n-1}(\alpha)$
右侧检验：$\frac{\bar{\theta} - \theta_0}{S/\sqrt{n}} \leq t_{n-1}(\alpha)$
双侧检验：$|\frac{\bar{\theta} - \theta_0}{S/\sqrt{n}}| \leq t_{n-1}(\alpha/2)$

In [5]:

Copied!





# 正态与t的区别：t尾部更厚
x=np.linspace(-6,6,200)
pdfb=st.norm.pdf(x,0,1)
t=st.t.pdf(x,5)
print(st.t.ppf(0.025,5))

plt.plot(x,pdfb,x,t)
plt.fill_between(x,pdfb,where=(x>1.96)|(x<-1.96),alpha=0.3)
plt.fill_between(x,t,where=(x>2.57)|(x<-2.57),alpha=0.3)
# 正态与 t 的区别：t 尾部更厚
x=np.linspace(-6,6,200)
pdfb=st.norm.pdf(x,0,1)
t=st.t.pdf(x,5)
print(st.t.ppf(0.025,5))

plt.plot(x,pdfb,x,t)
plt.fill_between(x,pdfb,where=(x>1.96)|(x<-1.96),alpha=0.3)
plt.fill_between(x,t,where=(x>2.57)|(x<-2.57),alpha=0.3)

-2.5705818356363146

Out[5]:

<matplotlib.collections.PolyCollection at 0x7f7395576300>

其他情况 ¶

两个正态分布的均值之差的检验，利用上节课的 $t_{n+m-2} 分布来检验

$$ \sqrt\frac{nm(n+m-2)}{n+m}\frac{\bar{x}-\bar{y} - (\mu_1-\mu_2)}{\sqrt{\sum_{i=1}^{n} (x_i-\bar{x})^2 + \sum_{i=1}^{m} (y_i-\bar{y})^2)}} \propto t_{n+m-2} $$

分布的 $\sigma^2$ 与 $\sigma^2_0$ 的比较 , 利用 $\chi^2$ 分布来检验

$$ \frac{(n-1)S^2}{\sigma^2} \propto \chi_{n-1}^2 $$

指数分布的均值，使用

$$ 2n\lambda\bar{x}\propto \chi_{2n}^2 $$

$$ \bar{x}< C,lambda>\lambda_0 $$

In [6]:

Copied!





rv=st.chi2(20)
x=np.linspace(rv.ppf(0.001),rv.ppf(0.999),200)
chi=rv.pdf(x)
l_alpha=rv.ppf(0.05)/20
r_alpha=rv.ppf(0.95)/20
l_alpha_2 = rv.ppf(0.025)/20
r_alpha_2 = rv.ppf(0.975)/20

print(l_alpha,r_alpha,l_alpha_2,r_alpha_2)
print(1/l_alpha,1/r_alpha,1/l_alpha_2,1/r_alpha_2)

plt.plot(x/20,chi)
### x*lambda0<1.57, 1/x>0.64*lambda_0 lambda > lambda_0
plt.fill_between(x/20,chi,where=(x/20>r_alpha),alpha=0.3)
### x*lambda0>0.54, 1/x<1.84*lambda_0 ,lambda < lambda_0
plt.fill_between(x/20,chi,where=(x/20<l_alpha),alpha=0.3)
### 0.47<x*lambda0<1.7, 0.58*lambda_0<1/x<2.08*lambda_0 ,lambda = lambda_0
plt.fill_between(x/20,chi,where=(x/20>r_alpha_2)|(x/20<l_alpha_2),alpha=0.3)
rv=st.chi2(20)
x=np.linspace(rv.ppf(0.001),rv.ppf(0.999),200)
chi=rv.pdf(x)
l_alpha=rv.ppf(0.05)/20
r_alpha=rv.ppf(0.95)/20
l_alpha_2 = rv.ppf(0.025)/20
r_alpha_2 = rv.ppf(0.975)/20

print(l_alpha,r_alpha,l_alpha_2,r_alpha_2)
print(1/l_alpha,1/r_alpha,1/l_alpha_2,1/r_alpha_2)

plt.plot(x/20,chi)
### x*lambda0<1.57, 1/x>0.64*lambda_0 lambda > lambda_0
plt.fill_between(x/20,chi,where=(x/20>r_alpha),alpha=0.3)
### x*lambda0>0.54, 1/x<1.84*lambda_0 ,lambda < lambda_0
plt.fill_between(x/20,chi,where=(x/20r_alpha_2)|(x/20

0.5425405697091296 1.570521642211546 0.4795388696132433 1.7084803451419166
1.8431801340425595 0.636731117306884 2.085336691906785 0.5853154839290434

Out[6]:

<matplotlib.collections.PolyCollection at 0x7f739767fe60>

符号检验 ¶

如果想确定地指导假设是否正确（普通的假设检验有可能得到矛盾的结论），需要根据 $\theta = \theta_0$ 的假设决策边界 $C_1,C_2$，若 $\theta < C_1$，认为 A 正确；$\theta > C_2$, 结论 B 正确

一个例子 ¶

在民意调查中，候选人 A 和 B 的得票情况通过以下方式确定：

民意测验 n 个人，得到人群中选 A 的人数 m，以计算选 A 的比例 p。
根据比例 p 的值，确定候选人 A 或 B 的胜选情况：
- 如果 p > 0.5，候选人 A 获胜。
- 如果 p < 0.5，候选人 B 获胜。
- 如果 p = 0.5，不能确定胜选情况。

在之前的计算中，1 和 2 之间存在重合的情况。根据 3 确定人数 m 的边界 C1, C2

当 C1 < m < C2 时，支持候选人 3。
当 m > C2 时，支持候选人 1。
当 m < C1 时，支持候选人 2。
m 服从二项分布 B(n, p)。

In [7]:

Copied!





n=10000
rv=st.binom(n,0.5)
x=np.arange(rv.ppf(0.001),rv.ppf(0.999))
chi=rv.pmf(x)
plt.plot(x,chi)
print(rv.ppf(0.025),rv.ppf(0.975))
plt.fill_between(x,chi,where=(x>rv.ppf(0.025)) & (x<rv.ppf(0.975)),alpha=0.3)
#binominal variance p*(1-p)*N
print(np.sqrt(0.5*0.5*n)*1.96)
n=10000
rv=st.binom(n,0.5)
x=np.arange(rv.ppf(0.001),rv.ppf(0.999))
chi=rv.pmf(x)
plt.plot(x,chi)
print(rv.ppf(0.025),rv.ppf(0.975))
plt.fill_between(x,chi,where=(x>rv.ppf(0.025)) & (x

4902.0 5098.0
98.0

根据结果我们可以发现，比 5000 人多不到 100 个人，我们就可以认为 A 胜出了

而二项分布的方差是 $np(1-p)$, 人数少的时候，方差更小