随机变量的数字特征 ¶
!!! note " 本文在 Immortal-Fates 的笔记和肖朦老师课件的基础之上修改；"
期望 | mean ¶
离散：$E(X)=\sum x_kp_k$
连续：$E(X)=\int_{-\infty}^{+\infty}xf(x)dx$
E(X) 必须收敛，无穷级数发散则不存在数学期望
- $X\sim N(\mu,\sigma^2), 标准正态变量 Z=\frac{X-\mu}{\sigma},E(Z)=0,Var(Z)=1,\\E(X)=\mu,Var(X)=\sigma^2$
随机变量函数的数学期望 ¶
$Y=g(X)$（连续函数）——可推广到多元
- 离散：$E(Y)=\sum g(x_k)p_k$
- 连续：$E(Y)=\int_{-\infty}^{+\infty}g(x)f(x)dx$
$Z=h(X,Y)$（连续函数）
- 离散：$E(Z)=\sum\sum h(x_i,y_i)p_{ij}$
- 连续：$E(Z)=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}h(x,y)f(x,y)dxdy$
不必管 Y 怎样，只用 X 即可算出
!!! note " 例 : 平均速度和平均时间。假设上学路途共 2 公里，天气好时（概率 0.6
特性 ¶
- 数学期望有线性性质
- 若 X，Y 相互独立，则 $E(XY)=E(X)E(Y)$
- 将 X 分解成数个随机变量之和，然后利用随机变量和的数学期望等于随机变量数学期望之和来求数学期望
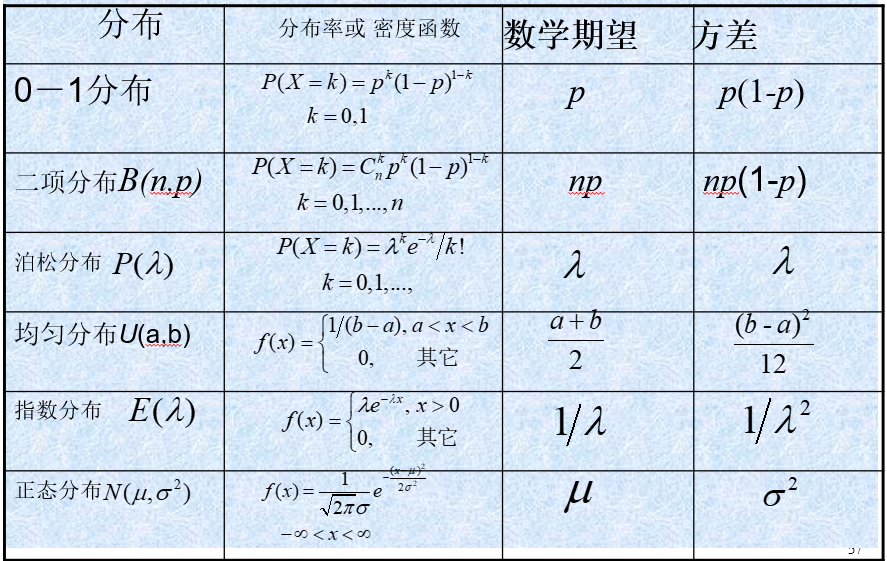
- 泊松分布的均值和方差都是 $\lambda$
方差 | variance ¶
定义 ¶
$Var(X)=E\{[X-E(X)]^2\}$，刻画分散程度
- 离散：$Var(X)=\sum [x_k-E(X)]^2p_k$
- 连续：$Var(X)=\int_{-\infty}^{+\infty}[x_k-E(X)]^2f(x)dx$
- $Var(X)=E(X^2)-[E(X)]^2$
- 标准差（均方差
） ：$\sigma(X)=\sqrt{Var(X)}$
性质 ¶
$Var(C)=0,Var(CX)=C^2Var(X)$
$Var(X+Y)=Var(X)+Var(Y)+2E\{[X-E(X)][Y-E(Y)]\}$
若 X，Y 相互独立，则 $Var(X+Y)=Var(X)+Var(Y)$
若 X，Y 相互独立：则 $Var(aX+bY+c)=a^2Var(X)+b^2Var(Y)$
独立的 n 个正态变量的线性组合仍服从正态分布
$C_0+C_1X_1+...\sim N(C_0+C_1\mu_1+...,C_1^2\sigma_1^2+C_2^2\sigma_2^2+...)$
np.var(x,ddof=1) # 样本方差
np.std(x,ddof=1) # 样本标准差
##计算均匀分布的各种数学特征
import scipy.stats as st
a,b=(0,10)
mean, var, skew, kurt = st.randint.stats(a,b+1, moments='mvsk') ## n阶中心矩
print(mean, var, skew, kurt)
print (st.randint.mean(a,b+1),st.randint.var(a,b+1))
5.0 10.0 0.0 -1.22 5.0 10.0
import numpy as np
import seaborn as sns
x=st.randint.rvs(a,b+1,size=1000)
sns.histplot(x,discrete=True)
print(st.randint.mean(a,b+1),np.mean(x))
print(st.randint.var(a,b+1),np.var(x,ddof=1)) # dof=n-1 为无偏估计 ddof 是 deduce degree of freedom
print(st.randint.std(a,b+1),np.std(x,ddof=1))
st.describe(x)
5.0 5.046 10.0 10.194078078078078 3.1622776601683795 3.192816637089903
DescribeResult(nobs=1000, minmax=(np.int64(0), np.int64(10)), mean=np.float64(5.046), variance=np.float64(10.19407807807808), skewness=np.float64(-0.003614673762058353), kurtosis=np.float64(-1.2515889974257615))
协方差 | covariance ¶
- 协方差：$Cov(X,Y)=E\{[X-E(X)][Y-E(Y)]\}$
- $Cov(X,Y)=E(XY)-E(X)E(Y)$
- 有线性性质（把 Cov 想象成内积）
- $Var(X+Y) = Var(X) + Var(Y) +2Cov(X,Y)$
协方差的性质：
$Cov(X, Y) = Cov(Y, X)$
$Cov(X, X) = \text{Var}(X)$
$Cov(aX, bY) = ab \cdot Cov(X, Y)$，其中 $a, b$ 为两个实数
$Cov(X_1 + X_2, Y) = Cov(X_1, Y) + Cov(X_2, Y)$
当 $\text{Var}(X) \text{Var}(Y) \neq 0$ 时，有
$$ (Cov(X, Y))^2 \leq \text{Var}(X) \text{Var}(Y) $$
其中等号当且仅当 $X$ 与 $Y$ 之间有严格的线性关系，即存在常数 $a, b$，使 $P(Y = a + bX) = 1$。
正态分布协方差：$\rho \sigma_1\sigma_2$
协方差矩阵 ¶
对于一个有 $n$ 个随机变量的随机向量 $\boldsymbol{X} = (X_1, X_2, \ldots, X_n)^T$，其协方差矩阵 $\boldsymbol{\Sigma}$ 是一个 $n \times n$ 的矩阵，其元素表示各个随机变量之间的协方差。
$$ \boldsymbol{\Sigma} = \begin{pmatrix} Cov(X_1, X_1) & Cov(X_1, X_2) & \cdots & Cov(X_1, X_n) \\ Cov(X_2, X_1) & Cov(X_2, X_2) & \cdots & Cov(X_2, X_n) \\ \vdots & \vdots & \ddots & \vdots \\ Cov(X_n, X_1) & Cov(X_n, X_2) & \cdots & Cov(X_n, X_n) \end{pmatrix} $$
对于任意两个随机变量 $X_i$ 和 $X_j$，其协方差 $Cov(X_i, X_j)$ 定义为：
$$ Cov(X_i, X_j) = E[(X_i - E[X_i])(X_j - E[X_j])] $$
其中，$E[X_i]$ 表示随机变量 $X_i$ 的期望值。
对于一个随机向量 $\boldsymbol{X}$，其协方差矩阵 $\boldsymbol{\Sigma}$ 也可以表示为：
$$ \boldsymbol{\Sigma} = E[(\boldsymbol{X} - E[\boldsymbol{X}])(\boldsymbol{X} - E[\boldsymbol{X}])^T] $$
其中，$E[\boldsymbol{X}]$ 表示随机向量 $\boldsymbol{X}$ 的期望向量，$(\boldsymbol{X} - E[\boldsymbol{X}])^T$ 表示 $(\boldsymbol{X} - E[\boldsymbol{X}])$ 的转置。
相关系数 ¶
线性关系紧密程度
$\rho_{XY}=\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}=Cov(\frac{X-E(X)}{\sqrt{Var(X)}},\frac{Y-E(Y)}{\sqrt{Var(Y)}})=\rho$
$|\rho_{XY}|\le 1$
$|\rho_{XY}| = 1 \Leftrightarrow$ 存在常数 $a, b$，使 $P(Y = a + bX) = 1$； 特别的，$\rho_{XY} = 1$ 时，$b > 0$；$\rho_{XY} = -1$ 时，$b < 0$
当 $\rho_{XY}>0$ 时，称 X 与 Y 为正相关
当 $\rho_{XY}<0$ 时，称 X 与 Y 为负相关
当 $\rho_{XY}=0$ 时，称 X 与 Y 为不相关或零相关
随机变量 $X$ 与 $Y$ 不相关，即 $\rho_{XY} = 0$ 等价条件有：
- $\text{Cov}(X, Y) = 0$
- $E(XY) = E(X)E(Y)$
- $\text{Var}(X + Y) = \text{Var}(X) + \text{Var}(Y)$
从而可知，当 $X$ 与 $Y$ 相互独立 $\Rightarrow X$ 与 $Y$ 一定不相关；反之，若 $X$ 与 $Y$ 不相关，$X$ 与 $Y$ 却不一定相互独立。
对于二元正态变量（X，Y）来说，X 和 Y 不相关等价于 X 与 Y 相互独立 注意变换，避免硬算
