运筹学复习总结 ¶

约 4182 个字预计阅读时间 16 分钟

课程信息

历年卷资料

2024 运筹学何衍班期末考试
 梁军2023-2024春夏学期运筹学回忆卷
 赵斐2023-2024春夏学期运筹学小测回忆
 17-18电气学院运筹学回忆 - CC98论坛
 18-19春夏运筹学试题回忆 - CC98论坛
 2021运筹学考试内容+复习方法集合 - CC98论坛
 2022夏学期控院运筹学 hy老师回忆卷 - CC98论坛
 2022年夏控院运筹学 lj老师回忆卷 - CC98论坛
 hy运筹学23夏回忆 - CC98论坛
 建筑工程学院《运筹学》2023-2024春夏备考经验 - CC98论坛
 2023-2024春电院运筹学期末回忆 - CC98论坛

pcgg 分享
 运筹学控院hy老师班笔记整理
 运筹学（控院何衍班）经验&资料分享
 《运筹学》lj老师班笔记整理
 2021-2022春夏管理学院-应用运筹学I（英文班）学习分享

知识是学不完的，最重要的是学习思想

为什么学习运筹学？ - 运筹学有丰富的优化思想与技术 - 提供科学管理和决策的方法

单纯形法原理 （要从原理上理解清楚以下情况的发生条件：唯一最优解、无穷多最优解、进一步迭代、迭代时换入变量和换出变量的条件、无界、无解、出现退化、下一步出现退化、需要对偶单纯形法计算、对偶问题最优值）只有这道题可能是填空或选择

对偶与对偶单纯形法 ( 互补松弛性 )

运输问题 （最小元素法 + 闭回路检验 / 伏格尔法 + 位势法检验，两种方法非最优时的闭回路调整）

整数规划——指派问题匈牙利法

目标规划问题 （只要求建模）

最短路问题 （狄克斯特拉算法）

最大流问题 （福特 - 富克逊法）

线性规划 ¶

建模 ¶

线性规划问题的标准形式

$C_n$ 为价值向量，$x_n$ 是约束变量，$A$ 是工艺矩阵，B 为约束向量

只能求最大值

\[ \begin{align*} max \quad &z = \mathbf{C}X\\ s.t. & \left\{ \begin{array}{lr} \mathbf{A} x = \vec{b} \\ x \ge 0 \end{array} \right. \end{align*} \]

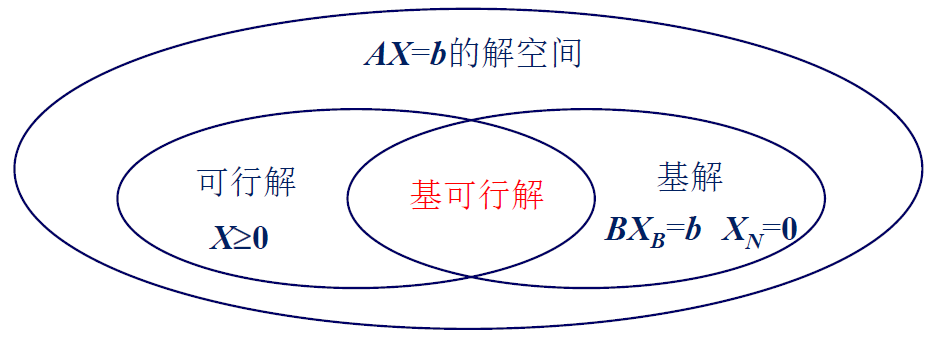
几何概念	代数概念
约束超平面	满足一个等式约束的解
约束半平面	满足一个不等式约束的解
约束半平面的交集	满足一组不等式约束的解
约束超平面的交点	基解
可行域的顶点	基可行解
目标函数等值面	目标函数值相同的解

单纯形法¶

线性规划最优解类型。单纯形法可求出哪种？

解的情况 :

唯一最优解：可以求

无穷最优解：可以求

无界解（少了约束）：无最优解

退化解：有约束没有效果

无可行解（约束矛盾，鱼与熊掌不可得兼）：

对偶问题 ¶

对偶问题的对偶怎么解释？举例说明

• 生产 : 目标函数追求利润最大化 , 约束方程设备的使用时长受约束 , 小于等于某个时间值 ; • 出租设备: 目标函数追求租金最小化 , 约束方程（机会成本）设备产生的利润要大于等于生产的利润 , 不能亏钱 ;

对偶问题的转化

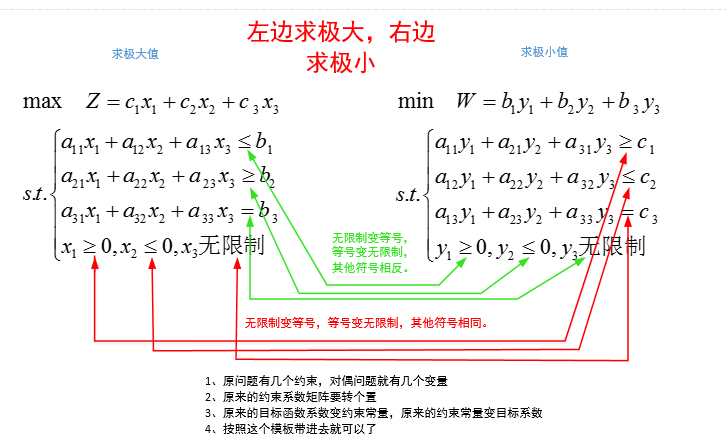
在这里插入图片描述

系数矩阵是转置

对偶问题对原问题有何帮助。举 3 例。

1. 证明原问题无界性

原问题为无界解，则对偶问题无可行解 ( 可以前推后，不可以后推前 )

互补松弛性求最优解

给了一个最终单纯性表，最终基变量是 x1，x2

（1）求最优解不变的 c1，c2 比值范围

（2）给 x1 增加一个必须是整数的条件，求最优解

整数规划 ¶

整数线性规划的种类

纯整数规划：$x_j$ 全部取整数的线性规划。
混合整数规划：$x_j$ 部分取整数的线性规划。
0-1 型整数规划：$x_j$ 只能取 0 或 1 的线性规划。

整数规划，松弛是什么意思？

松弛问题：放松原规划问题的整数条件所得到的新规划问题。

分支定界概念，意义。分枝定界法在混合整数和纯整数哪个更有效？

分枝：将原问题转化为子问题；

定界：确定界限减少搜索范围。

分支定界在混合整数中更有效，相当于只需要对其中的一部分进行分支。另一部分没有约束

线性规划 + 整数规划问题，给出一个线性规划问题的最优单纯形表。

（1）写出原问题的对偶问题；

（2）求原问题的最优整数解。

运输规划 ¶

运输问题建模的两种方法。

运输问题，给出问题的最优方案。

（1）问其中一个运价变化时，若最优方案不变，求该运价取值范围；

（2）问其中一个产地停产，最优方案怎么改变。

目标规划 ¶

思想：软约束 + 优先级

与线性规划区别

线性规划的目标是一个刚性的目标 . 但实际应用中，目标常常是模糊的；解决方法：建立软约束
线性规划立足于求满足所有约束条件的可行解，要求各个约束条件相容且可行域不是空集，而实际中的问题往往存在相互矛盾的约束条件 , 目标规划可在相互矛盾的约束条件下找到满意解 , 即满意方案 .
线性规划只能处理一个目标的问题 , 而目标规划能够统筹兼顾多个目标的关系求得更切合实际的解 .解决方案：设置优先级
目标规划找到的最优解是指尽可能达到或接近一个或多个已给定指标值的满意解
线性规划对约束条件是不分主次地同等对待 , 而目标规划可根据实际需要给予轻重缓急的考虑 .

现实生活中一般使用目标规划

2、目标规划问题，给出一个投资问题的背景。

（1）建立目标规划的模型，不需要求解；

（2）证明使用单纯形法求解目标规划问题时，可以忽略非线性约束 $d_i^++d_i^-=0$。

\[ \begin{align} \min z &= \mathop{\Sigma}\limits_{k=1}^K p_k [\mathop{\Sigma}\limits_{l=1}^L(w_{kl}^- d_l^- + w_{kl}^+d_l^+)]\\ s.t.&\left\{ \begin{array}{lr} \mathop{\Sigma}\limits_{j=1}^n c_{lj}x_j +d_l^- - d_l^+= g_l\\ \mathop{\Sigma}\limits_{j=1}^n a_{ij}x_j \le b_i\\ x_j \ge 0\\ d_l^-,d_l^+ \ge 0\\ \end{array} \right. \end{align} \]

条件	结果
$f(x) = g$, 恰好达到目标值	$\min z = f(d^+_k + d_k^-)$
$f(x) \ge g$，超过指标值，正偏差不限制，负偏差尽量小	$\min z = f(d_k^-)$
$f(x) \le g$，不超过指标值，负偏差不限制，正偏差尽量小	$\min z = f(d_k^+)$
当实际值确定只会大于目标值时	$d_i^+>0$，而 $d_i^-=0$
当实际值确定只会小于目标值时	$d_i^->0$，而 $d_i^+=0$。
实际值等于目标值时	$d_i^+=d_i^-=0$
任何一种情况	$d^+ \cdot d^- = 0$

$d^+$ 和 $d^-$不可能同时是基变量；无论怎么变换，都是相反数的关系

有哪两种求解方法

单纯形法
序贯法

有 K 个优先级，先按照第一个优先级求得最优值

将已计算目标函数值，作为下一级目标的硬约束。

再求第二优先级的最优值

目标规划能否用于非线性规划，为什么

三台发电机，分别有最大发电功率，最小发电功率，单位功率电价；

三个目标

P1：机组最大功率大于等于一个数

P2：两台发电机工作

P3：机组发电功率等于 $Lq$ 时，发电成本最小，建立数学模型

非线性规划 ¶

等式约束化为无约束问题有哪两种方法，各有什么特点？数值解的时候哪个更好。

大于等于和小于等于

动态规划 + 非线性规划问题，给出一个非线性规划问题。

（1）用动态规划方法求解；

（2）用 KT 条件求解。

给出题目问题的 KT 条件。判断是否为充要条件。原因。

KKT 条件的几何解释，什么时候充分？

凸函数时候充分必要

KKT 条件是判断某点是极值点的必要条件，不是充分条件。换句话说，最优解一定满足 KKT 条件，但KKT 条件的解不一定是最优解。

对于凸规划，KKT 条件就是充要条件了，只要满足 KKT 条件，则一定是极值点，且得到的一定还是全局最优解。

在最优解 X处，f(X*) 和 g(X*) 的梯度方向共线且方向相反。向量共线且方向相反* 在数学上的写法就是：

负梯度向量是另一个梯度向量的 $lambda$ 倍。移项后发现，这不就是KKT 条件的第一个等式嘛！ $$ nabla f(X^) +lambda nabla g(X^) = 0, lambda ge 0 $$

局部最优与全局最优的意义？单纯形法和最速下降分别收敛到哪个，为什么？

单纯形法：单纯形法是一种用于求解线性规划问题的迭代算法。它通过在可行域的顶点之间移动，逐步逼近最优解。在线性规划问题中，如果最优解存在，那么它一定是可行域的顶点之一。因此，单纯形法的收敛点是全局最优解。
最速下降法：最速下降法是一种用于求解无约束优化问题的迭代算法。它通过沿着目标函数梯度的反方向移动，逐步逼近最优解。最速下降法的收敛点取决于目标函数的类型和初始点的选择。
如果目标函数是凸函数，那么最速下降法的收敛点是全局最优解。因为在凸函数中，局部最优解和全局最优解是一致的。
如果目标函数是非凸函数，那么最速下降法的收敛点可能是局部最优解。因为在非凸函数中，存在多个局部最优解，而最速下降法可能会陷入其中之一。

选择迭代方向：最速下降法，牛顿法，共轭梯度法。这三种方法适合在寻优的哪个时期使用，为什么？

	优点	缺点	使用时期
最速下降法（负梯度方向）	计算量小	之字形迭代路径，接近极值点的时候尤为严重	迭代初期
牛顿法	极值点附近收敛速率快	计算量大，需要求二阶导数和 Hessian 矩阵逆。远离极值点时，不一定是下降方向，需采用进一步修正。	二次目标函数或极值点附近
拟牛顿法
共轭梯度法	所需存储量小，具有步收敛性，稳定性高克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算 Hesse 矩阵并求逆的缺点对于凸二次问题，$n$ 次就可以收敛	要存储，计算海森矩阵。对于非二次问题，存在极个别情况会无法达到收敛。

用内点法解析分析一个函数的最优解，并验证满足 KKT 条件

最小化函数 $f(x) = x_1 + x_2$，满足以下条件：

\[ \begin{aligned} -x_1^2 + x_2 &\geq 0 \\ x_1 &\geq 0 \end{aligned} \]

构造障碍函数 : $$ bar{P}(x, r)=x_{1}+x_{2}-r cdotleft[log left(-x_{1}^{2}+x_{2}right)+log left(x_{1}right)right] $$

根据驻点一阶条件 , 有

\[ \begin{array}{l} \frac{\partial \bar{P}}{\partial x_{1}}=1-r \cdot \frac{-2 x_{1}}{-x_{1}^{2}+x_{2}} \cdot r \cdot \frac{1}{x_{1}}=0 \\ \frac{\partial \bar{P}}{\partial x_{2}}=1-r \cdot \frac{1}{-x_{1}^{2}+x_{2}}=0 \end{array} \text { 求解得到: } \]

\[ \begin{array}{l} x_{1}=\frac{\sqrt{1+8 r}-1}{4} \\ x_{2}=\frac{3}{2} r-\frac{\sqrt{1+8 r}-1}{8} \end{array} \]

$r \rightarrow 0$ 时 , 有

\[ \left\{\begin{array}{l} x_{1}^{*}=0 \\ x_{2}^{*}=0 \end{array}\right. \]

动态规划 ¶

动态规划名词解释（状态、决策、阶段），举例解释。

阶段：问题过程按时间、空间的特征分解成若干相互联系的阶段。
状态：k 阶段开始（或结束）时的客观条件，记为 $s_k \in S_k$，$S_k$ 为 $k$ 阶段状态集合
决策：依据状态做出的决定，记为 $u_k(s_k)\in D_k(s_k)$ , $Dk (sk)$ 为状态 $s_k$ 的允许决策集合。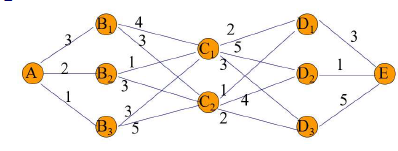如 $D_1(A) = {B_1,B_2,B_3},u_1(A) = B_i \quad i = 1,2,3$
状态转移方程：描述当前状态在给定决策下转移至下一阶段的过程；$s_{k+1}=T_k(s_k, u_k (s_k))$
指标函数: 评价沿子策略 $P_{k,n}$ 过程性能优劣的函数，记为 $V_{k,n}(s_{k}, p_{k,n})$。

状态无后向性，为什么？

状态的无后效性：给定某阶段的状态 $s_k$，则以后各阶段的状态 $s_l（l>k）$ 都只受 $s_k$ 的影响，与之前的状态无关。

已经求解的子问题，不会再受到后续决策的影响。

后部子过程策略，从 k 阶段开始到终了阶段的决策子序列，记为 $p_{s,n}(s_k) = \{u_k \left(s_k\right), u_{k+1}\left(s_{k+1}\right),\dots, u_n\left(s_n\right)\} \in P_{k,n} (s_k)$

动态规划的最优性原理指什么贝尔曼是如何用数学语言表达最优性原理的。

最优化原理：最优策略的子策略是对应子问题的最优策略。

最优化定理：策略 $p^*_{l,n}$ 是最优策略的充要条件是，对于所有的 k，都有：

\[ \begin{array}{lr} V_{1,n}\left({s_{l}}, p_{1, n}^{*}\right) \\ \quad=\mathop{opt}\limits_{p_{l, k-1} \in p_{l, k-1}} V_{1, k-1}\left(s_{1}, p_{1, k-1}\right)+\mathop{opt}\limits_{p_{k, n} \in p_{k, n}} V_{k, n}\left(s_{k}, p_{k, n}\right) \end{array} \]

贝尔曼最优方程描述了最优值函数 $V^{*}(s)$ 和 $Q^{*}(s,a)$ 之间的关系：

$V^{*}(s) = \max_{a} \left[ r(s,a) + \gamma \sum_{s'} P(s'|s,a) V^{*}(s') \right]$

其中，$\max_{a}$ 表示对于所有可能的动作 $a$ 取最大值，$s$ 是当前状态，$a$ 是动作，$r(s,a)$ 是状态 - 动作对的奖励，$\gamma$ 是折扣因子，$P(s'|s,a)$ 是状态转移概率。

建模给了一个差分方程和 x(0)=1，叫你求一个目标函数的最小值，用动态规划

图论 ¶

Dijkstra 算法  ¶

Dijkstra 算法公式及公式意义简述？能不能用来求最长路？

给了一个有向图（1）用 Dijkstra 法求最长路径（2）用动态规划建模

最短路问题，给出一个五个顶点的网络，用 Dijkstra 算法求其余各点到终点的最短路径。

数学推导

P(v_j)：表示到点v_j的最短距离。
T^{(k)}(v_j)：表示搜索到第k步时，到T点v_j的最短距离。
设定初值( 将起点以外距离都设置为无穷 )
$T^{(0)}(v_1) = 0$
$T^{(0)}(v_j) = \infty \quad j = 2, 3, ..., n$
确定 P 点（从所有未访问的点中，找出当前距离最小的）
$P(v_j) = \min\limits_j \{ T^{(k)}(v_j) \}$
更新 T 值（进行松弛操作）
$T^{(k+1)}(v_j) = \min\limits_i \{ T^{(k)}(v_j), P(v_j) + l_{ij} \}$ 其中，$l_{ij}$ 表示边的权重。

可以用于求最长路。

正权边图中求最长路可使用 SPFA
经典Dijsktra可在全负权边图中跑最长路、全正权边图中跑最短路；将所有边权全设置成为负数

Floyd¶

Floyd 算法对于网络边权有什么限定条件，为什么？

Floyd-Warshall算法不能处理带有负权环路的图，但它能够检测到负权环路的存在。

费用流 ¶

最小费用流问题，要求 V1 到 V2 的的最小流，V5 的 V6 的最小流情况下求最小费用

博弈论 ¶

Nash 均衡概念，此时是否为合作关系。

赢得矩阵 A=[(a11,4),(8,2)], 求 a11 的范围，使得局中人可以公布自己策略，为什么；若 a11 处于不能公布策略范围内，应该怎么办

排队论（没讲）¶

M/M/1/∞（1）证明单位时间内平均所有顾客逗留时间等于平均排队长（2）闲期花费 c1，每个顾客单位逗留时间花费 c2，求 ρ 使得总花费最小

存储论（没讲）¶

列举四个存储模型

条件	结果
\(f(x) = g\), 恰好达到目标值	\(\min z = f(d^+_k + d_k^-)\)
\(f(x) \ge g\)，超过指标值，正偏差不限制，负偏差尽量小	\(\min z = f(d_k^-)\)
\(f(x) \le g\)，不超过指标值，负偏差不限制，正偏差尽量小	\(\min z = f(d_k^+)\)
当实际值确定只会大于目标值时	\(d_i^+>0\)，而 \(d_i^-=0\)
当实际值确定只会小于目标值时	\(d_i^->0\)，而 \(d_i^+=0\)。
实际值等于目标值时	\(d_i^+=d_i^-=0\)
任何一种情况	\(d^+ \cdot d^- = 0\)