博弈论模型 ¶

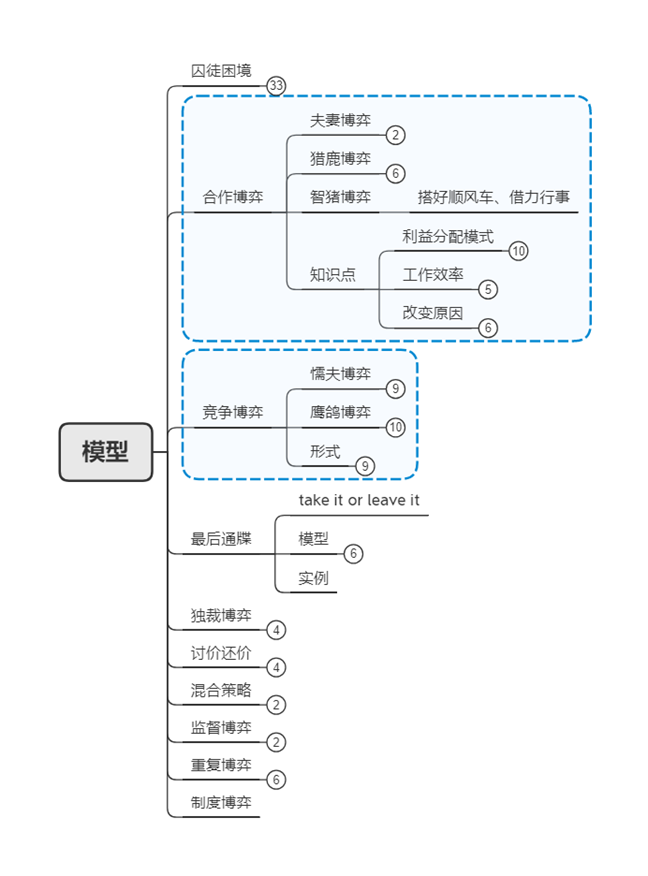
《博弈论基础》模型总结

A B	L	R
U	a, b	c, d
D	e, f	g, h

对于一个博弈模型来说，下面是收益矩阵的一般形式

囚犯困境模型 ¶

参数大小关系：a>e, b>d, ag, f>h

具体参数

AB	背叛	合作
背叛	中刑，中刑	释放，重刑
合作	重刑，释放	轻刑，轻刑

班级内卷就是一个经典的囚徒困境

AB	补习	不补习
补习	80，80	90，70
不补习	70，90	85，85

如果 A，B 都不补习，考试的难度不变，两个学生的成绩都是 85；

如果 A，B 都补习，考试的难度增加，两个学生得到的成绩都是 80；

如果 A, B 一个补习，一个不补习，补习的成绩 90，不补习的成绩 70

对于一方来讲，无论另一方补不补习，自己补习相对于自己不补习都是占优策略。占优策略均衡就是双方都补课。

所以均衡结果往往是绝大部分学生都补习，出题人不得不增加考题的难度以保持区分度，又促使学生增加补习来适应难度，如此恶性循环，学生压力增加，家长经济负担加重，出题人越来越难以出一份区分度明显的高质量考题，判卷老师必须增设更多的得分门槛，投入更多的精力来打出不同的分数。

再举一个生活中的例子，比如说男女生关系。

男生女生	不表白	表白
不表白	普通朋友	失败可能朋友没得做
表白	失败可能朋友没得做	在一起

对于两个人来说，都表白并在一起是整体的均衡解。但是吗，不论对于男生还是女生来说，在不知道双向暗恋的情况下，告白有一定的风险，若是告白失败，那么朋友显然就没得做了。所以博弈结果就是双方都会选择占优策略的均衡解，即双方都不表白。

性别战博弈 ¶

参数大小关系：a>b, g<h, max(c, d, e, f)≤min(b, g)

具体就是

丈夫 妻子	足球赛	看剧
足球赛	10，5	0，0
看剧	0，0	5，10

举宿舍熬夜的例子

室友 A 室友 B	不熬夜	熬夜
不熬夜	早睡，早睡 + 不快	冲突
熬夜	冲突	复习 + 第二天没精神，玩嗨

室友 A 想早睡觉，室友 B 想熬夜打游戏。

如果 A 先关灯，发挥先动优势，B 可能退让。

如果 B 先打游戏，发挥先动优势，A 可能宽容。

如果 A，B 约定哪几天一起熬夜，哪几天一起早睡，则在遵守约定的前提下整体均衡结果不会是冲突。

猎鹿博弈模型 ¶

参数大小关系：a>e>c, a>g, b>h>f, b>h

具体来讲

A B	猎鹿	猎兔
猎鹿	W+F，W+F	0, W
猎兔	W，0	W, W

以给彩礼收彩礼为例子

如今的许多婚姻家庭仍然存在着女方家属向男方家属索要彩礼的现象。假设存在这样的一对夫妻，如果男方主动给彩礼且女方主动要彩礼，则双方皆大欢喜，并且证明了经济实力，均得到 +10 的评价收益。而如果男方不主动给，女方也不主动索要，则双方依然均获益，但此时没有证明经济实力，故只有 +5 的评价收益。而如果一方给另一方不需要或者一方索要另一方不给，主动的一方往往会降低对对方的评价，同时又刻意抬高了自己的实力。

女方 男方	给彩礼	不给彩礼
要彩礼	10,10	-3,3
不要彩礼	3，-3	5,5

对男方来说，如果女方要彩礼，则其最佳策略是给彩礼，否则会降低对方对自己的评价；如果女方不要彩礼，其最佳策略是不给彩礼，否则会让对方认为自己霸道。对女方而言，最佳策略同样如此。

结合上述分析，其均衡是 ( 男方给彩礼，女方要彩礼 ) 和 ( 男方不给彩礼，女方不要彩礼 )。换句话说，在婚姻中，不论是否索要彩礼或者是否给予彩礼，都最好先和对方说清楚，让对方明知自己会怎么样，使这件事成为双方的共同知识，这样才能使得双方的博弈结果是婚后利益最大化，否则会导致婚后男方或女方单方面地感到压力。

感悟：

猎鹿博弈其实实现的是“1+1>2”的合作效果。

目前在世界上比比皆是的企业强强联合就很接近于猎鹿博弈的帕累托改善，跨国汽车公司的联合、日本两大银行的联合等等均属此列，这种强强联合造成的结果是资金雄厚、生产技术先进、在世界上占有的竞争地位更优越，发挥的影响更显赫。总之，他们将蛋糕做得更大，双方的效益也就越高。比如宝山钢铁公司与上海钢铁集团强强联合也好，最重要的就是将蛋糕做大。在宝钢与上钢的强强联合中，宝钢有着资金、效益、管理水平、规模等各方面的优势，上钢也有着生产技术与经验的优势。两个公司实施强强联合，充分发挥各方的优势，发掘更多更大的潜力，形成一个更大更有力的拳头，将蛋糕做得比原先两个蛋糕之和还要大。

智猪博弈 ¶

参数大小关系：a>e, c>g, b>d, h>f

背景介绍 ¶

猪圈里有两头猪，一头大猪，一头小猪。猪圈的一边有个踏板，每踩一下踏板，在远离踏板的猪圈的另一边的投食口就会落下少量的食物。

如果有一只猪去踩踏板，另一只猪就有机会抢先吃到另一边落下的食物。当小猪踩动踏板时，大猪会在小猪跑到食槽之前刚好吃光所有的食物；若是大猪踩动了踏板，则还有机会在小猪吃完落下的食物之前跑到食槽，争吃到另一半残羹。

均衡分析 ¶

收益矩阵为：

大猪 小猪	等	按
等	0,0	9,1-A
按	6-A,4	7-A,3-A

A是按按钮所消耗的能量

当 A 不同时，均衡解也不同。

• \(A≥7\) 时（走去吃饭的路上就饿死）

大猪去按按钮的收益必定小于等于不按的收益，大猪不想去。小猪去按按钮的收益必定小于不按的收益，小猪也不想去。均衡结果是（0，0），即两头猪都会饿死。

• 其中，当 \(A≥10\) 时，都不去按的整体收益最大。

• 当 \(7＜A＜10\) 时，尽管去按的整体收益大于不去按的整体收益，但两头猪都觉得自己去按不划算，所以都不想去。

大猪 小猪	等	按
等	0,0( 都饿死 )	9,<0
按	<0,4	<0,<0

• 当 \(6≤A≤7\)

小猪去按的收益必定小于不去按的收益，觉得不划算，小猪选择不去按。大猪聪明，知道小猪不想去按，但自己去按的收益小于等于不去按的收益，觉得也不划算，大猪也不想去按。均衡结果还是（0,0）

大猪 小猪	等	按
等	0,0( 都饿死 )	9,<0
按	<0,4	0~1,<0

• 当 \(1≤A＜6\) 时，是智猪博弈的经典情况，以 A=2 为例。

从大猪的角度来分析，如果大猪选择等待，小猪会怎么做？此时小猪如果等待，收益是 0；如果行动，收益小于 0。无论怎么选择，小猪都只能饿死，所以当大猪等待时，小猪的最优策略是等待，大家一起饿死。大猪也深知小猪的选择，所以大猪要想不被饿死，只能选择行动。

既然大猪无论如何都只能行动，那小猪还有行动的必要吗？如果小猪等待，收益是 4；如果行动，收益是 1，显然小猪最佳的策略仍然是等待。

由此可见，大猪行动，小猪等待，是智猪博弈必然走向的局面。这个局面，也被称为智猪博弈当中的纳什均衡点。

大猪 小猪	等	按
等	0,0	9,-1
按	4,4（均衡）	5,1

• \(A＜1\) 时

大猪小猪谁去按都能落着吃的，但等着另一边去按更划算，所以均衡结果是（9，1-A）和（6-A，4）

大猪 小猪	等	按
等	0,0	9,1-A（均衡）
按	6-A,4（均衡）	7-A,3-A

以团队合作为例，假设 A 是大佬，B 是菜鸡

A B	摸鱼	干活
摸鱼	奖金 0+ 摸鱼，奖金 0+ 摸鱼	奖金 9w+ 摸鱼，奖金 1w+996
干活	奖金 9w+996，奖金 1w+ 摸鱼	奖金 7w+996，奖金 3w+996

7w 的奖金不值得 996 时，大佬的收益必定小于等于不按的收益，大佬选择摸鱼。摸鱼党去干活的收益必定小于不按的收益，摸鱼党也选择摸鱼。均衡结果是这个团队都摸鱼，任务停摆。

其中，当 10w 的奖金不值得 996 时，都不去干活的整体收益最大。

当 996 的价值在 7w 和 10w 之间时，尽管干活的整体收益大于不去按的整体收益，但团队成员都觉得自己干活不划算，所以都不想去，任务停摆。

当 996 的价值在 6w 和 7w 之间时，摸鱼党去干活的收益必定小于摸鱼的收益，觉得不划算，摸鱼党选择摸鱼。大佬知道摸鱼党想摸鱼，但自己干活的收益小于等于摸鱼的净收益，觉得也不划算，大佬也想摸鱼，任务还是停摆。

当 996 的价值在 1w 和 6w 之间时，摸鱼还是觉得去干活不划算，摸鱼党选择摸鱼，大佬知道干活总比摸鱼好点，所以选择干活。整体均衡结果为（大佬奖金 9w+996，摸鱼党奖金 1w+ 摸鱼） ，任务完成。

当 996 的价值小于 1w 时，谁干活都划算，但等着另一边去干更划算，所以整体均衡结果为（大佬奖金 9w+996, 摸鱼党奖金 1w+ 摸鱼）或者（大佬奖金 7w+996, 摸鱼党奖金 3w+996），任务完成。

感悟：

其实智猪博弈就是一个“多劳者不多得”的例子，由二八定律可以告诉我们，团队合作中，80% 价值是由 20% 的人创造的人。所以在一个项目中，大部分人都会是“小猪”，而真正有能力的人是“大猪”。

所以在实际的团队合作管理中，我们首先要根据团队目标对工作进行分解，再根据团队各个成员的职责、能力和任务将团队目标落实到个人工作目标。也一定要能识别大猪和小猪，在平衡中前进，大家都有饭吃。

必要时也要采取激励机制，正向激励让大家们明白什么样的行为才是团队期望的行为（例如按按钮的行为）。对于大猪，及时给予奖励从而肯定其行为，使之继续保持下去并进一步调动其积极性。

负向激励用来告诉团队成员什么样的行为是不可以做的（例如小猪只会等待的行为）。对于那些工作偷懒，产出不佳，甚至危害团队合作的小猪，采用批评、处罚等方式，杜绝某类行为的再次发生。

作为大猪，要在一定程度上接纳小猪搭便车。因为大猪的最优策略其实是让自己更值钱。你做得越多，你的成长越快，越值钱，有朝一日离开这个失衡的环境，你就越有可能找到更好的机会，获取更多的回报。从这个角度讲，充当大猪的那些任劳任怨的工程师，更看重的是做事的机会，通过在公司的平台上做事，最终成就自己。哪怕在一个小猪众多，看起来付出与收获不成比例的环境里也能成就自己。

作为小猪，应当尽量通过发挥自己某方面的能力与大猪建立良好的合作关系，与大猪形成有效的互补，这样才能一起前进，跟着大猪取得更大的成就！

懦夫博弈 ¶

参数大小关系：a<e<g<c, b<d<h<f

具体来讲

A B	进攻	退让
进攻	A-C，A-C	2A,0
退让	0，2A	A,A

A>C，则两人都进是均衡

A<C，则先下手为强。如果是同时博弈，那么选进的概率为 A/C

竞争博弈的三个特点：换位思考（情商）、高人一筹（智商）、胜负难料（逆商）。

l C 对博弈结果的影响：

计算一下均衡收益。均衡情况下我选“进”和“退”的期望收益是一样的，那么就以选“退”为例，此时对方“退”的概率为 1-A/C，我的期望收益就是 A(1-A/C) 从中可以看出，C 增大时双方期望收益增大。也就是说，如果双方斗起来的损失都比较大，打起来的概率较小，对双方有利。

l A 对博弈结果的影响

上面计算得到的期望收益为 A(1-A/C)，关于 A 是一个开口朝下的抛物线，最高点在 C/2 处取到。

重赏之下，必有莽夫！赢者通吃，导致过度竞争！

例子 ¶

以冷战期间古巴导弹危机为例

古巴导弹危机

美国 苏联	部署导弹	撤回导弹
部署导弹	战争一触即发	领先，被超越
撤回导弹	被威胁，威胁	保持和平

古巴导弹危机可以说是史上玩得最大的“懦夫博弈”。1962 年，苏联在古巴境内秘密部署核导弹，由此美苏双方不断升级威慑手段，战争一触即发。但经过 13 天的针锋相对，双方最终互相妥协，苏联撤走了部署在古巴的导弹，美国也保证不再入侵古巴并撤回其部署在土耳其和意大利的导弹。在这场危机中，双方都不断“在危险的边缘试探”，以此恐吓对方妥协而避免两败俱伤的结果。

感悟：

懦夫博弈的逻辑是“不要命的最大”，因为如果两人都拒绝转弯而任由两车相撞，那么最终将会两败俱伤、谁都无法收益。故而谁坚持直行到最后，而逼迫对方做出改变，谁就是游戏中的赢家。

混合博弈和监督博弈 ¶

参数大小关系 : b<0, e<0, f<0，h>0, g>0, f>-a

具体点，就是

雇主 雇员	偷懒	不偷懒
检查	F-C, -F	V-W-C, W-H
不检查	-W, W	V-W, W-H

其中，H<WC-F

纳什均衡的混合策略解为雇员偷懒概率 H/(W+F)

​ 雇主检查概率 C/（W+F）

当雇主支付的工资额为 (CV)^(½)-F 时，雇主的期望收益最大。

雇主的期望收益为 V-2(CV)^(½)+F，雇员的期望收益为 W-H

双方总期望收益为 V-H-CV/(W+F)，当 W=(CV)^(½)-F。

结论：V 越大，雇主给的工资越高。

C 越大，雇主给的工资越高。

F 越大，雇主给的工资越高。

当 W 越大 , 雇主的检查概率下降 , 雇员的偷懒概率也会下降。高薪养廉的含义即在此。

当 F 越大 , 雇主的检查概率下降 , 雇员的偷懒概率也会下降。乱世用重典的含义即在此。

当 H 越大 , 雇主的检查概率增加 , 雇员的偷懒概率不变。越是难以完成的工作 , 越需要雇主加强监督。

当 C 越大 , 雇主的检查概率不变 , 雇员的偷懒概率增加。越是难以监督的工作 , 雇员就越会偷懒。

例子 ¶

以上微积分课堂师生点名

A B	不来教室	来教室
点名	F-C，-F	V-W-C, W-H
不点名	-W, W	V-W, W-H

纳什均衡的混合策略解为不来教室概率 \(H/(W+F)\)

​ 老师点名概率 \(C/(W+F）\)

老师点名有效的期望为 \(V-2(CV)^(1/2)+F\)

来教室的期望收益为 W-H

双方总期望收益为 \(V-H-CV/(W+F)\)

最后通牒博弈模型 ¶

提议者 表决者	同意	拒绝
提出分配比例	按比例分配	0，0

以社团中采访任务的分工为例，

我作为项目小组的负责人，首先在项目群中发布了一个调查大家哪天有空的问卷，发现大家选择的选项比较分散，不能得出一个统一的结果。

所以我召开了一个线上会议，经过讨论后，给出两个日期（周五或者周日）让大家进行选择（最后通牒），经过大家选择之后，选择了周五晚上作为项目执行的时间。

这样提高了沟通的效率，节省了我们的沟通成本。