规划论 | Mathematical Programming ¶
约 8147 个字 预计阅读时间 32 分钟
线性规划 ¶
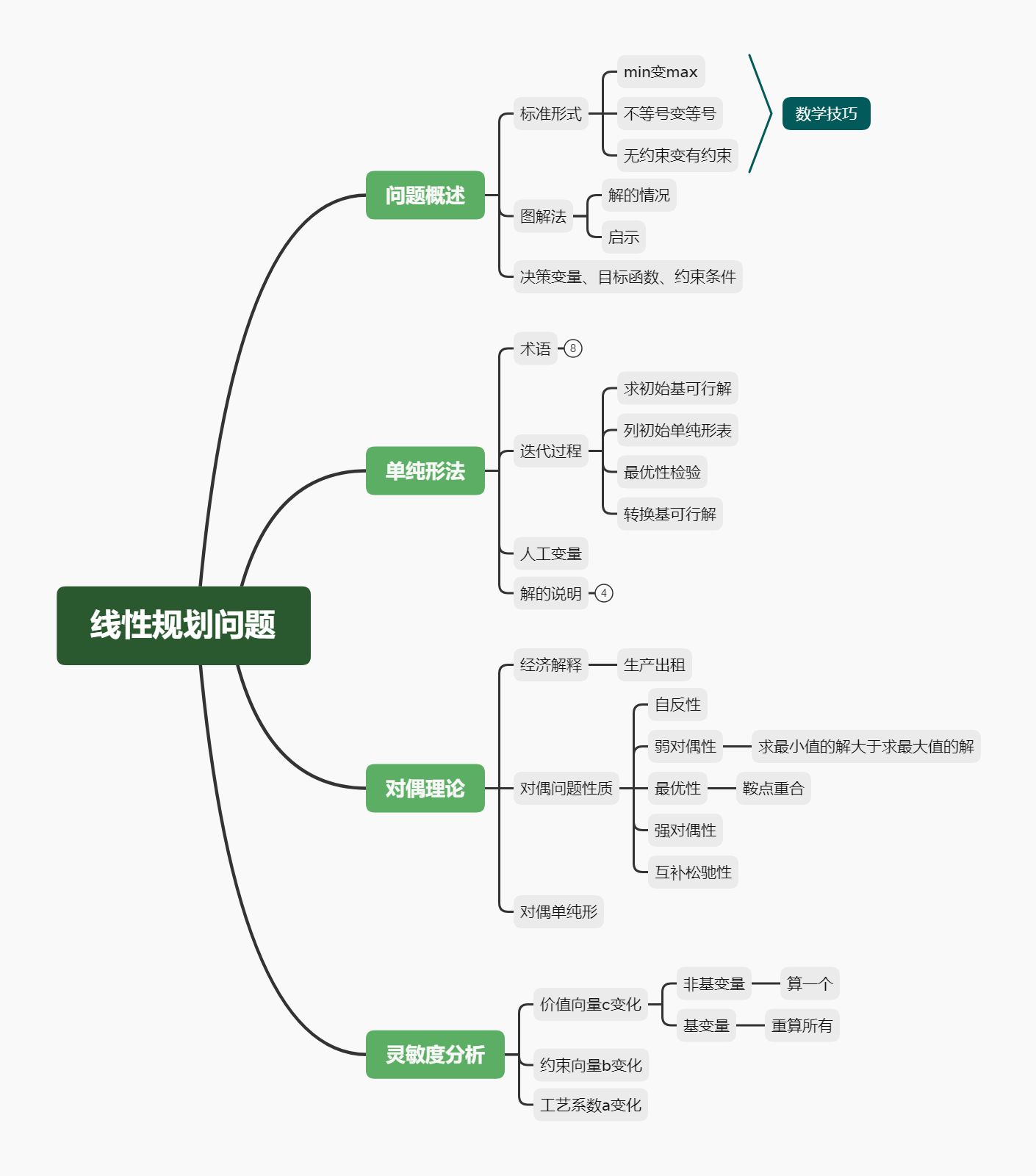
基础 ¶
\(C_n\) 为价值向量,\(x_n\) 是约束变量,\(A\) 是工艺矩阵,B 为约束向量
图解法:找到可行域,移动平行直线
从图解法我们可以发现有以下规律
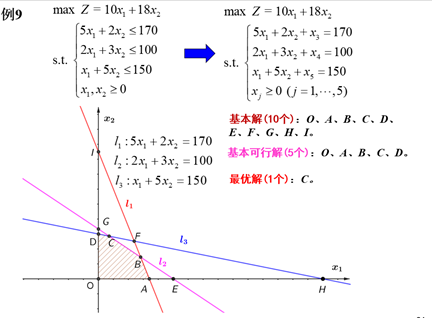
- 解的情况 : 唯一最优解、无穷最优解、无界解(少了约束)无可行解(约束矛盾,鱼与熊掌不可得兼)
- 可行域很可能是一个凸集
- 最优解若存在,很可能就是可行域的顶点
数学表述与标准形式 ¶
线性规划问题的一般数学模型可以表示为:
目标函数:maximize ( 或 minimize) \(Z = c_1x_1 + c_2x_2 + \cdots + c_nx_n\)
约束条件:
- \(a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n \leq b_1\)
- \(a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n \leq b_2\)
- \(\cdots\)
- \(a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n \leq b_m\)
- \(x_1, x_2, \cdots, x_n \geq 0\)
\(C_n\) 为价值向量,\(x_n\) 是约束变量,\(A\) 是工艺矩阵,B 为约束向量
矩阵方式表示为:
\(Z = \begin{bmatrix} c_1 & c_2 & \cdots & c_n \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \mathbf{c}^T \mathbf{x}\)
约束条件:
\(\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \leq \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix}\)
即 \(\mathbf{A}\mathbf{x} \leq \mathbf{b}\),以及非负约束:
线性规划问题的标准形式¶



变量条件转化为标准约束 $$ begin{align} x_j ge 0 quad unchange\ x_j le 0 quad x_j' = -x_j\ x_j no limit quad x_j'ge 0,x_j''ge 0,x_j = x_j'-x_j'' end{align} $$
约束条件的转化
把不等式条件转化为等式条件
大于等于则减去松弛变量
绝对值不等式换成两个不等式
目标函数的转化
拉格朗日方程不可以用
\(x\ge 0\) 这个条件不可以用求极值的方法
定义
在线性规划问题中,可行域是指满足所有约束条件的区域。换句话说,可行域包含了所有可行的解,即满足所有约束条件的解。
数学表示:对于线性规划问题 \(\max Z = \mathbf{c}^T\mathbf{x}\),约束条件为 \(\mathbf{A}\mathbf{x} \leq \mathbf{b}\) 且 \(\mathbf{x} \geq \mathbf{0}\),其可行域可以表示为:
其中,\(\mathcal{F}\) 表示可行域,\(\mathbb{R}^n\) 表示 \(n\) 维实数空间。
凸集是指集合中任意两点之间的线段仍然属于该集合的集合。
换句话说,如果集合中任意两点 \(\mathbf{x}\) 和 \(\mathbf{y}\),以及任意实数 \(\lambda \in [0, 1]\),都有 \(\lambda\mathbf{x} + (1-\lambda)\mathbf{y}\) 属于该集合,那么该集合就是凸集。
数学表示:对于集合 \(\mathcal{S} \subseteq \mathbb{R}^n\),如果对于任意 \(\mathbf{x}, \mathbf{y} \in \mathcal{S}\) 和任意 \(\lambda \in [0, 1]\),都有 \(\lambda\mathbf{x} + (1-\lambda)\mathbf{y} \in \mathcal{S}\),那么集合 \(\mathcal{S}\) 是一个凸集。
不出现在任意两点的连线内
凸集的顶点是指凸集中不能被表示为其他点线性组合的点。换句话说,顶点是凸集中的极值点,无法通过凸集中其他点的线性组合来得到。
数学表示:对于凸集 \(\mathcal{S} \subseteq \mathbb{R}^n\),如果存在点 \(\mathbf{x} \in \mathcal{S}\),使得对于任意 \(\mathbf{y}, \mathbf{z} \in \mathcal{S}\) 和任意 \(\lambda \in (0, 1)\),都有 \(\lambda\mathbf{y} + (1-\lambda)\mathbf{z} \neq \mathbf{x}\),那么点 \(\mathbf{x}\) 是凸集 \(\mathcal{S}\) 的一个顶点。
满足 \(\mathbf{A}x = \vec{b}\\x\ge 0\) 的解 \(\mathbf{x} = (x_1,\dots,x_n)^T\) 是可行解。
可行解的集合叫可行域。目标函数最值叫最优解
系数矩阵 \(\mathbf{A}=(a_{ij})_{m\times n}\) \(rank(A)=m\),\(\mathbf{B_{m \times m}}= (p_1,p_2,\dots,p_m)\) 是 A 的非奇异子矩阵,B 称为基
基 \(\mathbf{B_{m \times m}}= (p_1,p_2,\dots,p_m)\) 的向量 \(p_j\) 称为基向量,其他称为非基变量
约束方程变为
令 \(x_j=0,\quad j=\left[ m+1,n\right]\)
基解为解向量\(\mathbf{x} (x_1,\dots,x_m,0,\dots,0)^T\)
非基变量设为零,解出的基变量的值
基解中 \(\mathbf{x} \ge 0\) 的解
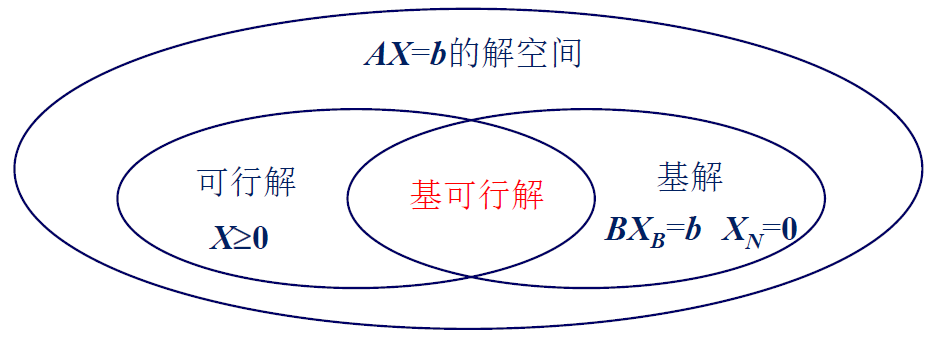
定理 1 若线性规划问题存在可行解,则问题的可行域是凸集
引理 1 若 \(rank(A)=m\),则可行解 \(x\) 为基可行解
可行解 x 的正分量所对应的系数列向量线性独立
必要性证明:基可行解的定义
充分性证明:
可行解x是基解,构造x对应的基
假设x正分量个数为k,可知\(k\le m\)
- 如果 \(k=m\),可直接视正分量对应的列向量为基;
- 如果 \(k<m\),总可补充 \(m-k\) 个列向量构成基。
定理 2 线性规划的可行域顶点与基可行解一一对应
考察逆否命题:\(x\) 不是可行域顶点 \(\iff\)\(x\) 不是基可行解
1)\(x\) 不是基可行解 \(\Rightarrow\) \(x\) 不是可行域顶点
可行解\(x\)不是基可行解
\(\Rightarrow\) \(x\)正分量对应的系数列向量线性相关
构造两个可行点
\(\Rightarrow x\)为两可行点的凸组合
\(\Rightarrow x\)不是顶点
基本可行解有两个关键因素:
- 所有约束均满足。
- 存在 n 个线性无关的约束有效。
顶点在约束所限制的多面体内,因此所有约束也都是满足的。下来考虑第二个关键因素,存在 n 个线性无关的约束有效,则说明这个点在 n 个超平面的交上。注意:n 维空间中 n 个线性无关的超平面的交是一个点
。 (比如:2 维空间中,两条线性无关的线的交是一个点;三维空间中,三个线性无关的面的交也是一个点) 。那这个点为什么会是在多面体的最外侧而不是内部呢?这是因为多面体是由半空间所构成的,而上述的超平面就恰好是多面体的最外侧的面。那么基本可行解落在的点也就恰好是多平面的一个顶点。


定理 3 若线性规划问题有最优解,一定存在一个最优解是基可行解
| 几何概念 | 代数概念 |
|---|---|
| 约束超平面 | 满足一个等式约束的解 |
| 约束半平面 | 满足一个不等式约束的解 |
| 约束半平面的交集 | 满足一组不等式约束的解 |
| 约束超平面的交点 | 基解 |
| 可行域的顶点 | 基可行解 |
| 目标函数等值面 | 目标函数值相同的解 |
一、基本单纯形法 ¶
博客
【运筹学】单纯形法总结 ( 单纯形法原理 | 单纯形法流程 | 单纯形表 | 计算检验数 | 最优解判定 | 入基变量 | 出基变量 | 方程组同解变换 ) ★★★-CSDN 博客
详细步骤解答【Wu 的课堂
】 《运筹学》单纯形法中文讲解 _ 哔哩哔哩 _bilibili非常清楚的视频 讲的非常好四种解的特殊情况
思想
解必然存在于顶点处,那么只需要验证顶点就可以了,但是一个一个验证很麻烦,所以采用相邻迭代
先求出一个基本可行解,判断是否最优;不是最优的话再换一个基本可行解
松弛化为标准形式:通过添加松弛变量将不等号化为等号,并保证所有变量都大于等于 0。找到一组单位矩阵
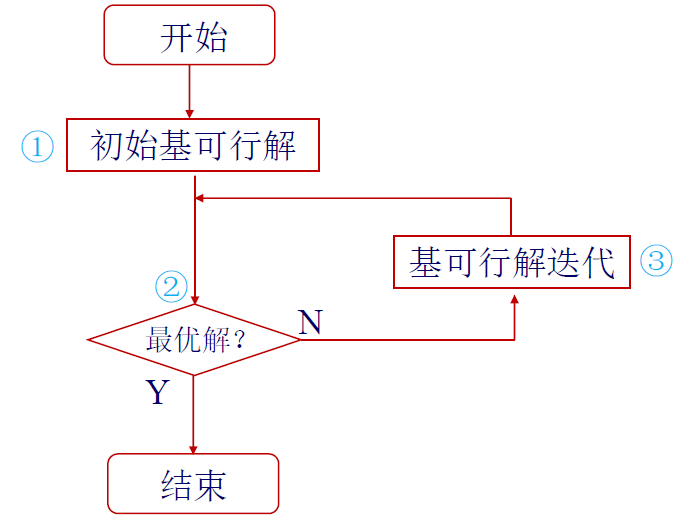
找初始基可行解¶
通常通过构造某一部分单位矩阵来找到初始基可行解。
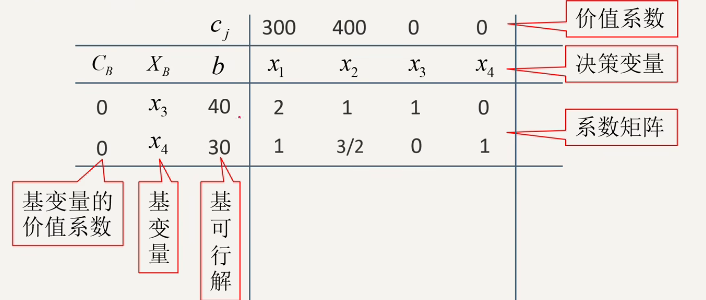
单纯形表的解释
单纯形表的各个元素的含义
基变量对应检验数必为 0
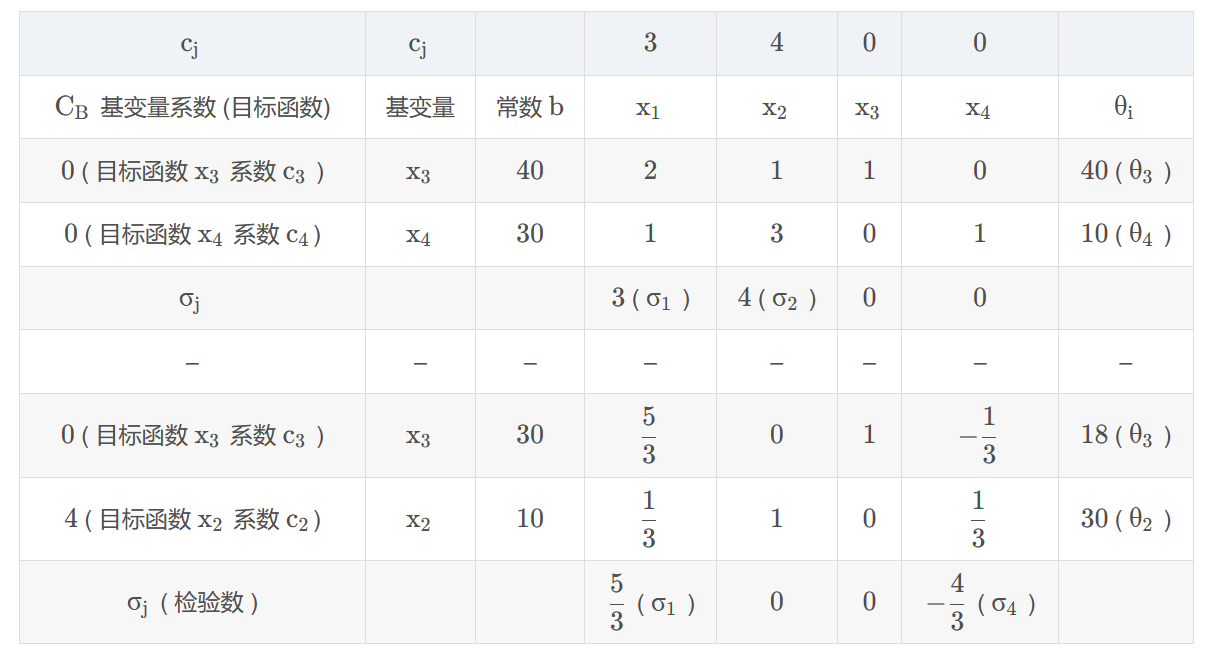
最优性检验¶
计算检验数 \(\sigma\),即目标函数系数与对应基变量系数的差值。根据最终的检验数结果判断是否有唯一解、无穷解或无解。
\(\sigma_j = c_j - \Sigma^m_{i=1} c_ia_{ij}\)
没有大于 0 的最优值时候,跳出循环
- 若非基变量检验数全小于 0,有唯一可行解
- 多重解:若存在一个非基变量检验数为 0,则有无数可行解
可以将为 0 的非基变量作为入基变量再进行一次,得到另一个解
其他的最优解使用 \(X_1^*\) 和 \(X_2^*\) 的线性组合 \(X^* = \alpha X_1^*+(1-\alpha) X_2^*\) 求得。
目标函数平行于非冗余的紧约束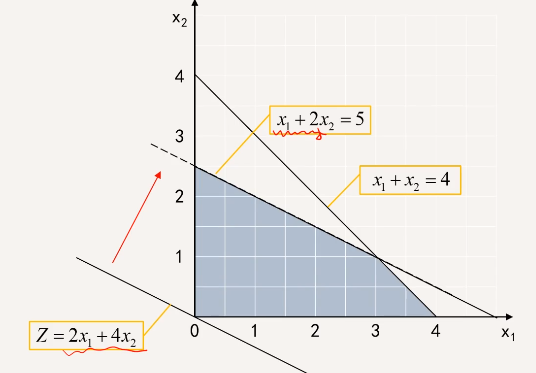
- 无界解:若检验数 \(\sigma_k >0\) 且对应的变量 \(x_k\) 系数列向量 \(P_k \le 0\),则有无界解。
原因:计算 \(\theta_i\) 无法计算,要么小于 0,要么不能除,所以找不到出基变量
约束条件不够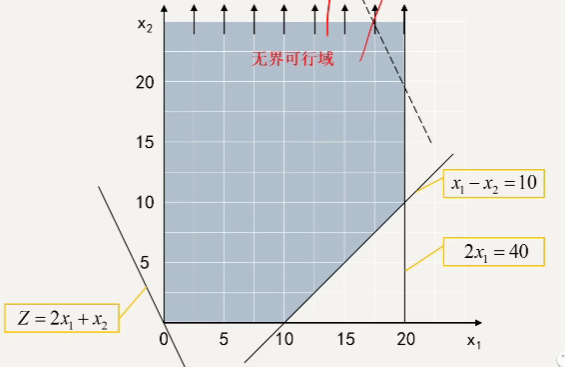
- 退化解:有多个相同的 \(\theta_i\)时候,下一次迭代会有基变量等于 0
原因:有约束没有作用,有冗余约束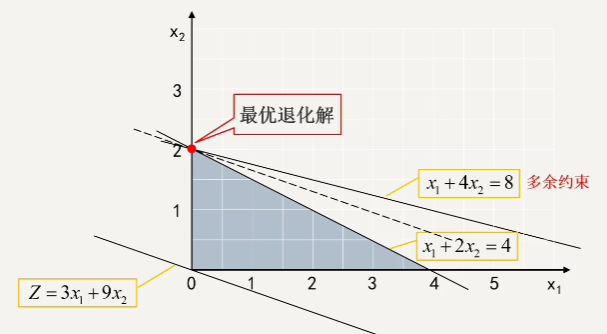 元素相同时候,选择下角标最小的作为出基变量入基变量
元素相同时候,选择下角标最小的作为出基变量入基变量 - 无可行解:检验数小于 0,但又不等于零的人工变量
; (有矛盾的约束)
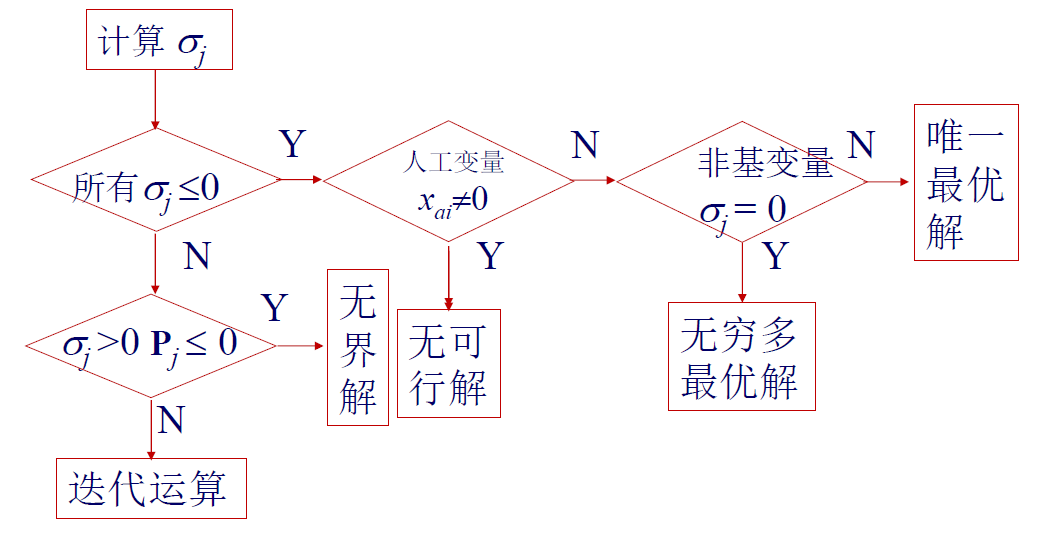
基可行解迭代¶
每次都只变更一个基向量
- 入基变量:按检验数最大选取
- 出基变量:按 \(\theta_i = \frac{b_i}{a_{lk}}\)最小选取 \(\theta = min \{ \frac{b_i}{a_{ik}}\}\)
- 初等行变换
需要 \(a_{lk}>0\)
\(x_i-\theta \cdot a_j\),若 \(a_j<0\), 那么 \(\theta\) 可以取到无穷大
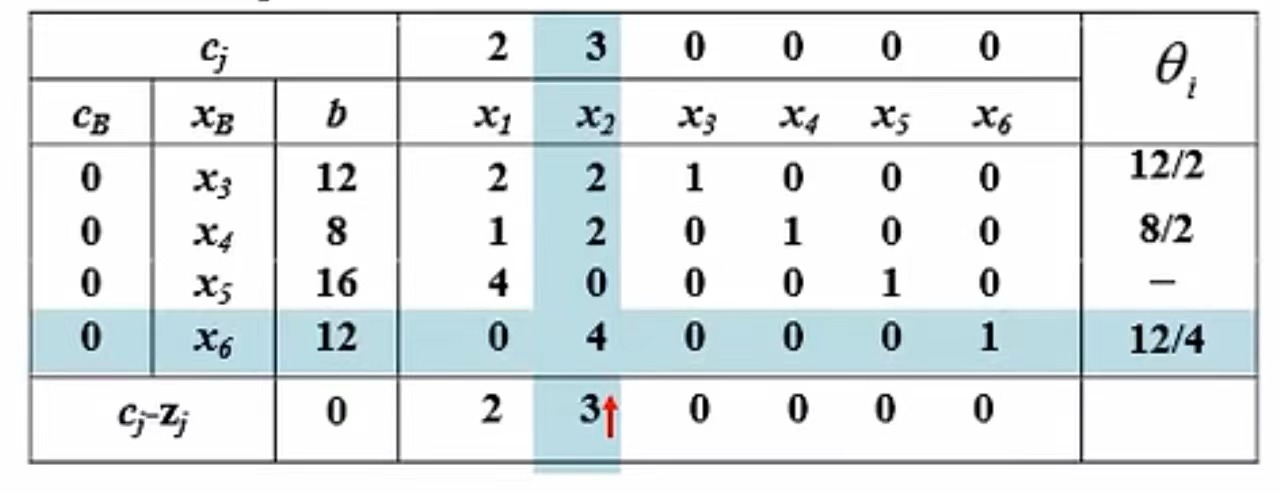
相邻基可行解的非基变量仅有一个不同
退化:基变量出现零的现象
影响:可能出现循环迭代
二、人工变量法
线性规划要是有最优解,人工变量为 0
使人工变量为 0,让人工变量出基
人工变量法是在无法直接找到单位矩阵作为起始时使用的一种方法,主要步骤包括:

- 引入人工变量:人为引入几个人工变量使其构成对角单位矩阵。
- 目标函数引入 M:为了防止引入人工变量对线性规划的最大、最小解产生影响,在目标函数中引入一个正无穷的 M。
计算检验数
与基本单纯形法类似,计算检验数来确定入基和出基变量。
- 所有检验数小于零且没有人工变量,则有最优解
-
所有检验数小于零,有非零人工变量,没有可行解。
-
中心元变换:在迭代过程中将人工变量替换成其他已有的变量,如果无法将人工变量替走,则无可行解。

二、对偶理论 ¶
参考博文
背景理解 ¶
• 生产 : 目标函数追求 利润最大化 , 约束方程设备的使用时长受约束 , 小于等于 某个时间值 ; • 出租设备 : 目标函数追求 租金最小化 , 约束方程(机会成本)设备产生的利润要 大于等于 生产的利润 , 不能亏钱 ;
对偶问题最优解 \(y^*_1,y^*_2\dots y^*_m\) 称为影子价格,影子价格是一种机会成本。影子价格大于市场价格,可买入,否则卖出。
\(y_i^* = \frac{\partial{z^*}}{\partial{b_i}} = \frac{最大利润增量}{第i种资源增量} = 第i种资源边际利润\)
- 边际利润大于 0,资源都要被用掉
- 有剩余的资源,边际利润 =0
- 机会成本 > 利润,不安排生产
感性理解:曲面的鞍点
两个问题的解相反但是
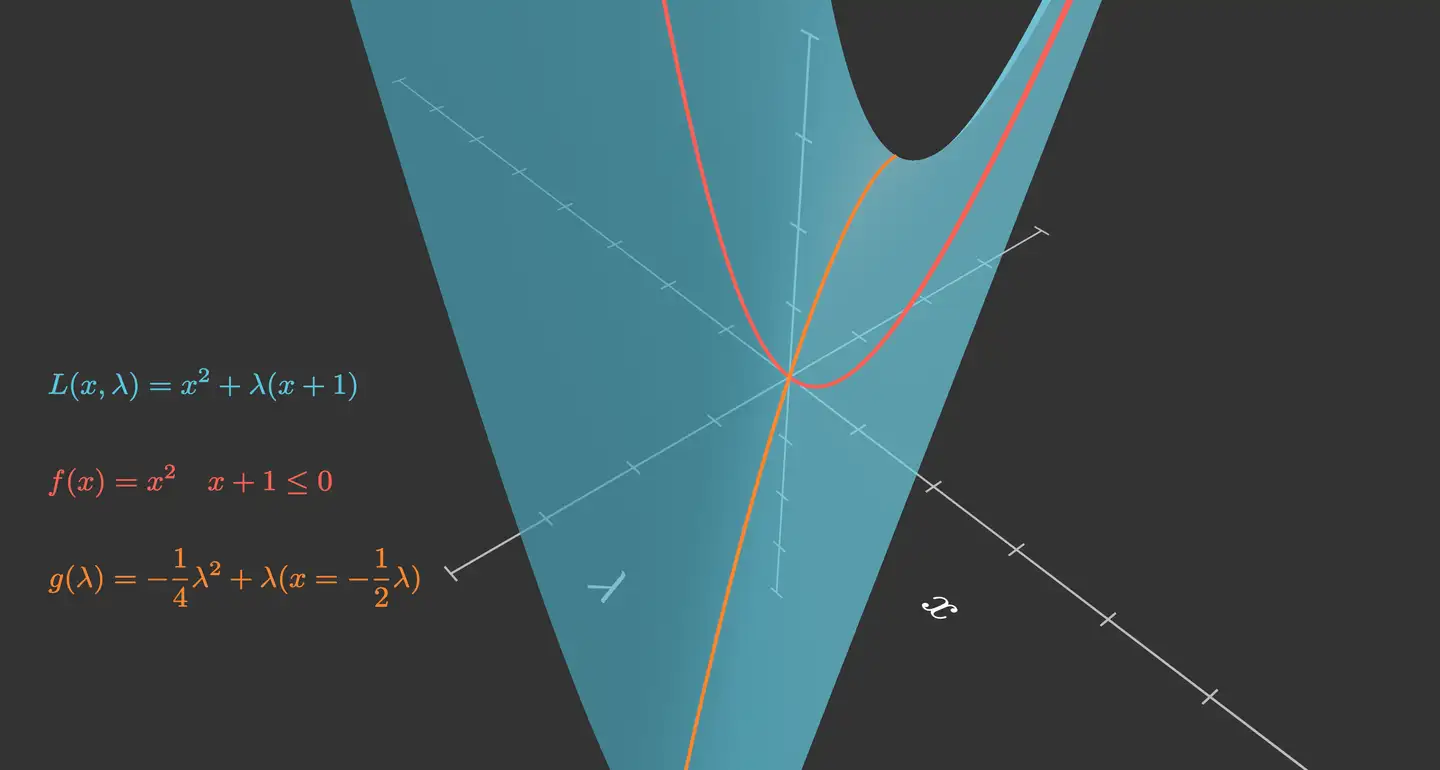
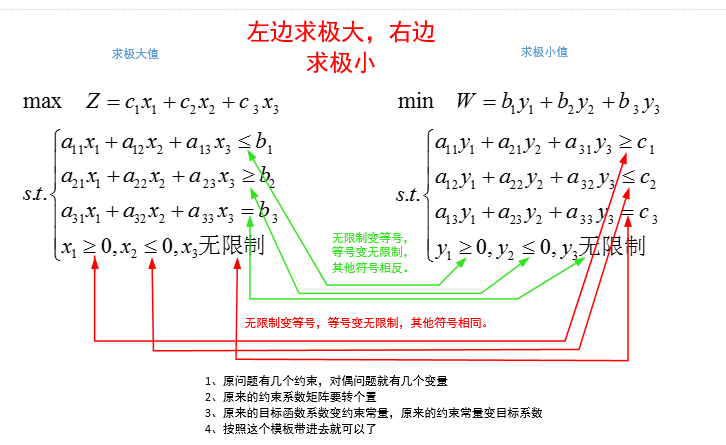
对称性定理 ¶
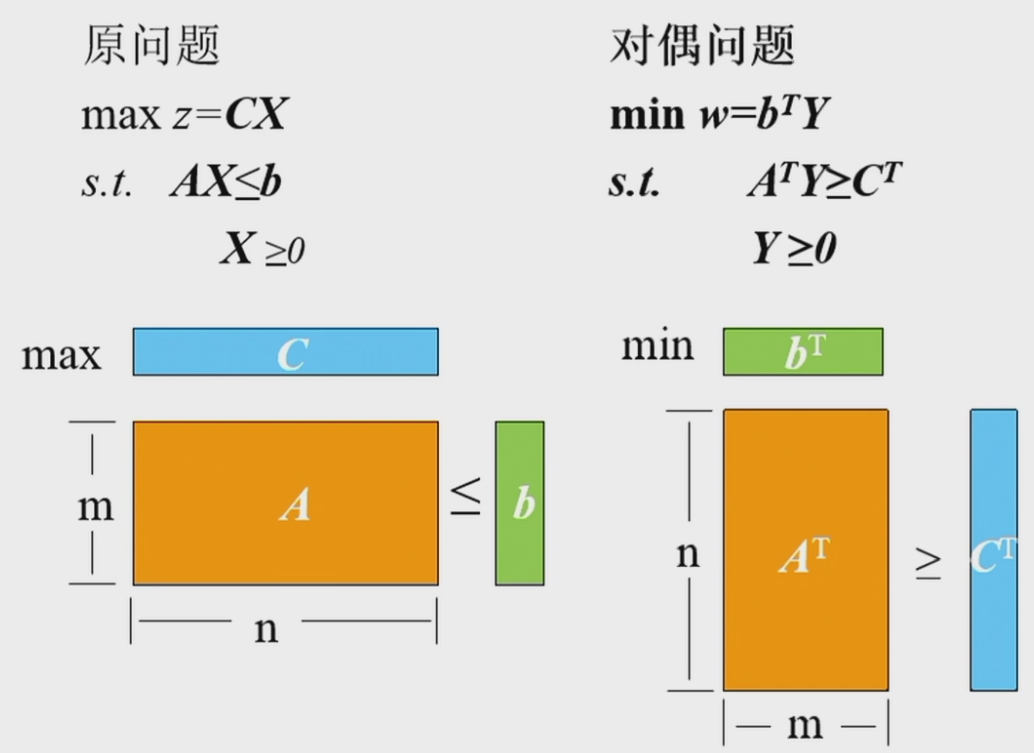
原问题 和 对偶问题 互为对偶 ; 对偶问题是对称的
原问题(Primal Problem
其中,Z 是目标函数,c 是目标函数的系数向量,x 是决策变量向量,A 是约束矩阵,b 是约束向量。
对偶问题(Dual Problem
其中,W 是对偶目标函数,y 是对偶变量向量。
弱对偶性(Weak Duality)¶
若 \(\overline{x}\) 是原问题 ( 目标函数求最大 ) 的可行解,\(\overline{y}\) 是对偶问题(目标函数求最小)的可行解
则 \(c^T\overline{x} \leq b^T\overline{y}\)。
最优解是相同的,所以求最小值的大于求最大值的
推导
设 \(x_0,y_0\) 分别是原始问题和对偶问题的可行解,那么有 \(z = cx^0 \le y^{0T}A x^0 \le y^{0T}b = w\)
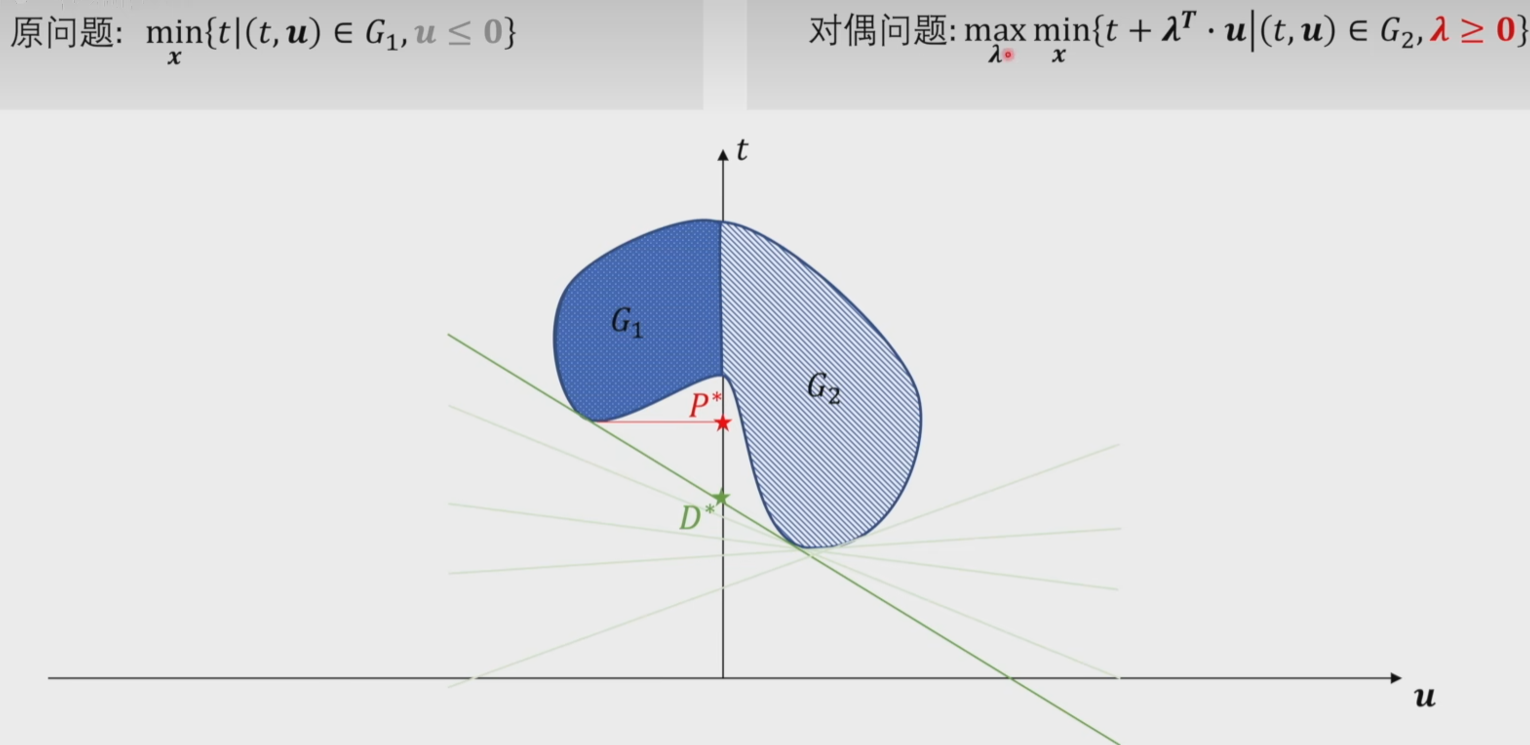
弱对偶定理推论 1:
原问题任何一个可行解的目标函数值 , 都是其对偶问题目标函数值的下界 ;
对偶问题任何一个可行解的目标函数值 , 都是其原问题目标函数的上界 ;
弱对偶定理推论 2:( 对偶问题的无界性 )
原问题为无界解,则对偶问题无可行解
可以前推后,不可以后推前


弱对偶定理推论 3:
在一对对偶问题 (P) 和 (D) 中 ,
如果其中一个线性规划问题可行 , 而另一个线性规划问题不可行 , 则该可行问题的目标函数是无界的 ;
最优性(Optimality)¶
若 \(\overline{x}\) 是原问题的可行解,\(\overline{y}\) 是对偶问题的可行解,且 \(c^T\overline{x} = b^T\overline{y}\)
则 \(\overline{x}\) 是原问题的最优解,\(\overline{y}\)是对偶问题的最优解
证明
设 \(x^*,y^*\) 分别是原始问题和对偶问题的最优解
有\(cx^0 \le cx^* \le b^T y^*\le b^T y^0\)
所以当\(cx^0 = b^T y^0\)时候,有\(cx^0 = cx^* = b^T y^*= b^T y^0\)
强对偶性(Strong Duality)¶
若原问题和对偶问题都有可行解,则它们都有最优解,
且最优解的目标函数值相等,即 \(c^Tx^* = b^Ty^*\)
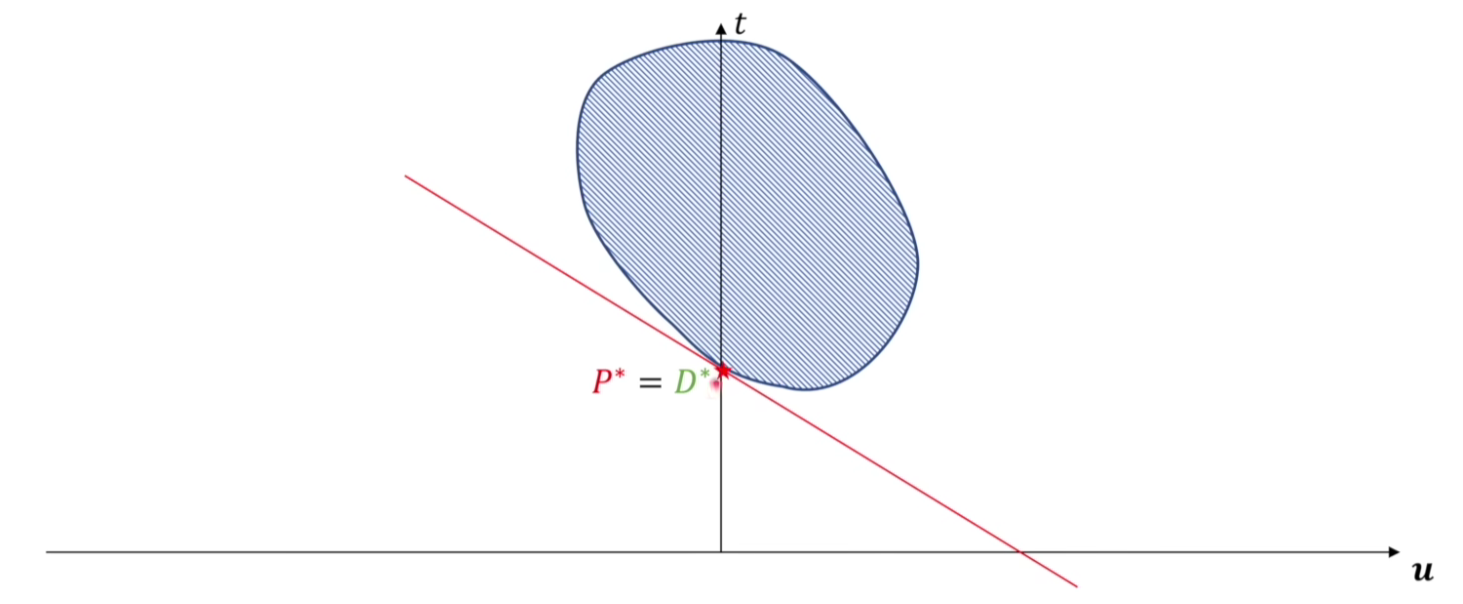
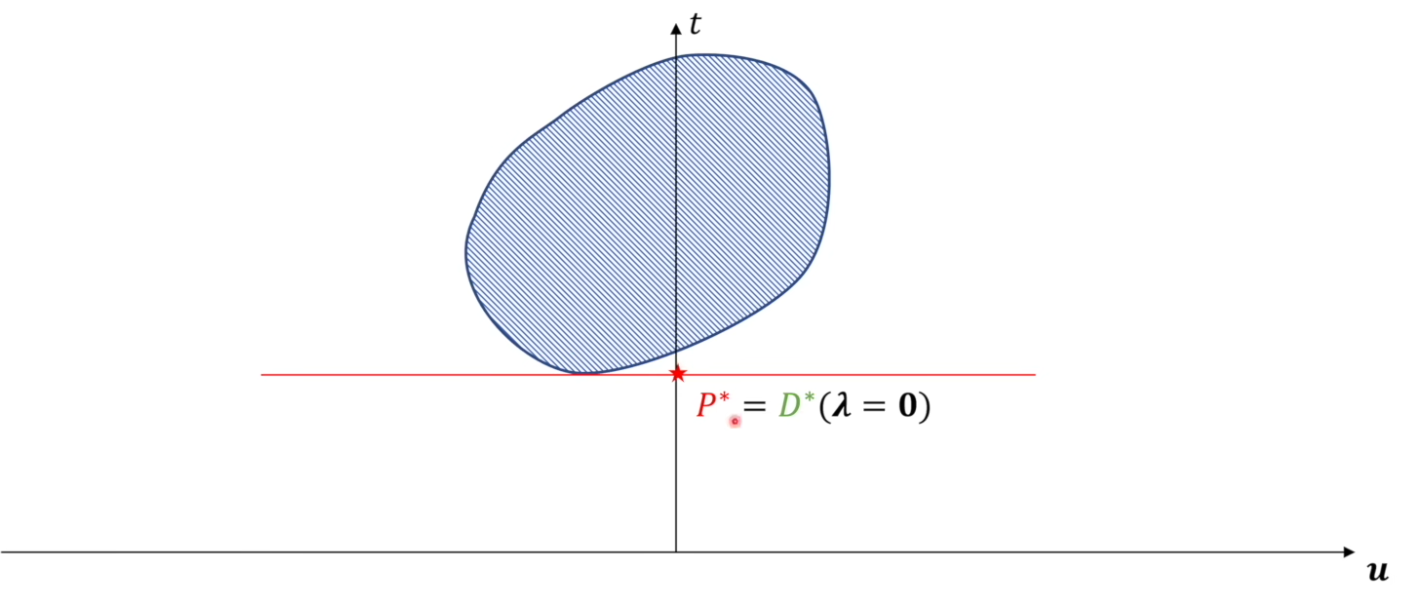
证明
由弱对偶性可知,原问题的目标函数值有上界,对偶问题的目标函数值有下界,故有最优值
设原问题的最优解为\(x^*\)时,\(x_B^* = \mathbf{B^{-1}} b\),由单纯形法矩阵分析,可知\(y = (c_B B^{-1})^T\)是一个可行解
满足\(w = b^T y = c_B B^{-1}b = c_B x_B^* = cx^* = z^*\)
| 初始单纯形表 | c | 0 |
|---|---|---|
| \(0\ x_s\ b\) | \(\mathbf{A}\) | \(\mathbf{I}\) |
| \(\sigma_j\) | c | 0 |
| 最终单纯形表 | c | 0 |
|---|---|---|
| \(c_B \ x_B \ B^{-1}b\) | \(B^{-1}A\) | \(B^{-1}\) |
| \(\sigma _j\) | \(c-c_BB^{-1}A\) | \(-c_B B^{-1}\) |
因为最终检验数都小于 0,所以 \(c_B B^{-1} \ge 0,y = (c_B B^{-1})^T \ge 0\),且有 \(c-c_BB^{-1}A \le 0\\ c_BB^{-1}A \ge c\), 所以 y 是一个可行解
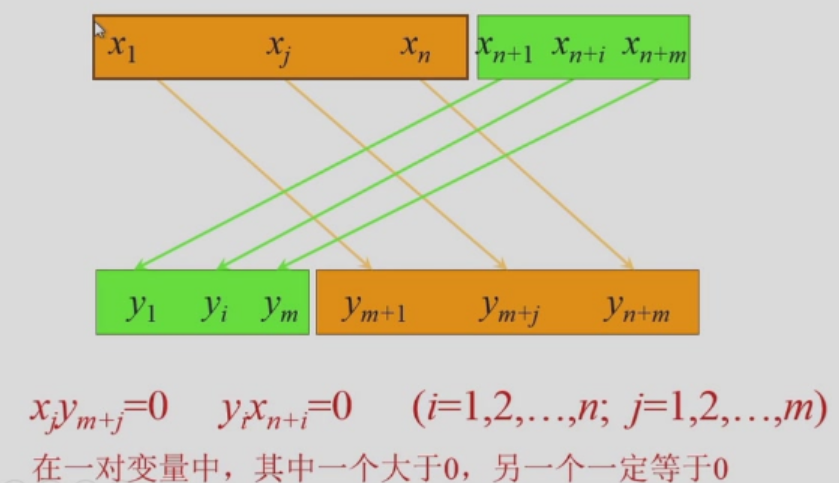
互补松弛性(Complementary Slackness)¶
\(\hat{X},\hat{Y}\) 是原问题和对偶问题的可行解,\(X_s,Y_s\) 是松弛变量的可行解,
则 \(\hat{X}\) 和 \(\hat{Y}\) 是最优解当且仅当 \(Y_s\hat{X} = 0,\hat{Y}X_s = 0\)
给了 m+n 个方程,互补松弛定理的等式
2、对偶松弛定理: 先将问题的对偶解算出来,得到对偶解的值(条件1),代入对偶问题的不等式可得到对偶问题不等式是否为严格不等式(条件2)
条件 1:说明对偶问题的解如果不为 0,原问题的对应解为等式(即 AX-b=0)
条件 2:反之如果将对偶问题解代入可得为严格不等式,则原问题的对应解为 0。

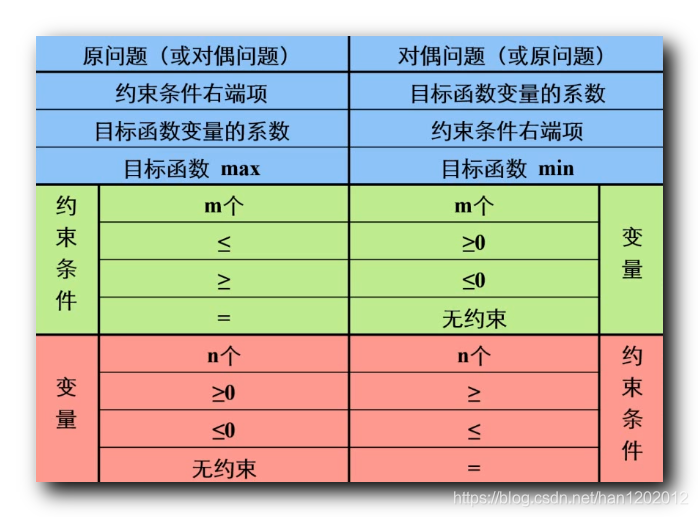
约束条件的转化 ¶
一个问题的约束和对偶问题的变量有关系
| 原问题 | 对偶问题 |
|---|---|
| 约束 | 原变量 |
| 原变量 | 约束 |
| 松弛变量 | |
| 松弛变量 | 原变量 |
| 基解 | 检验数 |
| 检验数 | 基解 |
系数矩阵是转置

对偶单纯形法 ¶
单纯形表上,原问题的检验数对应对偶问题的一个基解,相反数关系 ;
单纯形表同时给出原问题和对偶问题的基解。
单纯形表的解释:保持 x 可行解,y 演变为可行解
证明
对偶问题的约束方程 \(A^Ty-y_s = c^T\)
记录\(A = [B\ N]\quad y_s= [y_{sB}^T \ y_{sN}]\)
对偶单纯形法,是原始单纯形法
步骤 1:构造初始可行解
构造一个对偶问题的初始可行解,要求全部检验数 \(\sigma_j\le0,\sigma_j = c_j-\sum\limits^m_{i=1}c_ia_{ij}\)
步骤 2:相邻基可行解迭代
所有 \(b_i>0\),已经是最优解
- 取 \(x_r\) 出基变量,\(b_r = \mathop{min}\limits_i\{b_i<0\},i = 1,\dots,m\)
- 入基变量 \(x_s\),\(\theta' = \frac{\sigma_s}{a_{rs}} = \mathop{min}\limits_i\{\frac{\sigma_j}{a_{rj}}|a_{rj} <0,j = 1,\dots,n\}\)
所有 \(a_{ij}\ge0\)
说明对偶问题无界解
步骤 3:跳出循环
可行性分析
如上选取的目的:保持 \(\sigma_j ' \le 0\), \(y\) 为可行解
分析: \(\sigma_j ' = \sigma_j - \frac{a_{rj}}{a_{rs}}\sigma_s = a_{rj}\left(\frac{\sigma_j}{a_{rj}}-\frac{\sigma_s}{a_{rs}}\right)\)
因为 \(\sigma_j \ge 0\), \(a_{rs}\) 为主元素,有 \(a_{rs} < 0\),
当 \(a_{rj} \ge 0: \sigma_j / a_{rj} \ge 0, \sigma_s / a_{rs} \ge 0\), 所以 \(\sigma_j ' \le 0\)
当 \(a_{rj} < 0: \sigma_j / a_{rj} - \sigma_s / a_{rs} \ge 0\), 所以 \(\sigma_j ' \le 0\)
- 初始解可以是非可行解,当检验数都 \(\le0\) 时候,就可以进行基变换,不需要添加人工变量
- 当变量多于约束条件的时候,用对偶单纯形法可减少计算工作量
- 用于灵敏度分析及求解整数规划的割平面法
三、灵敏度分析 ¶
最优解在参数、约束条件或变量个数发生变化时候的影响
- 参数变化的情况,最优解怎么变
- 最优解 / 最优基不变时候,参数变化的范围
【运筹学】- 对偶理论与灵敏度分析 ( 三 )( 灵敏度分析 )_ 哔哩哔哩 _bilibili
原问题可行解就是满足 \(b\ge 0\)
对偶问题可行解的条件是满足最优性检验条件,求最大(Max)的时候,\(\sigma_i <0\)(不能再增加了)
| 原问题 | 对偶问题 | 处理 |
|---|---|---|
| 可行解 | 可行解 | 最优解 / 最优基不变 |
| 可行解 | 非可行解 | 用单纯形法迭代求解 |
| 非可行解 | 可行解 | 用对偶单纯形法迭代求解 |
| 非可行解 | 非可行解 | 重新编制单纯形表 |

原问题可行解,\(b\ge0\)
对偶问题可行解,\(\sigma \le 0\)
① \(b\) 的变化:\(x_B=B^{-1}b\)
\(\mathbf{B}^{-1}\) 是松弛变量对应的技术系数
② \(c\) 的变化:
\(\sigma_A=c-c_BB^{-1}A \quad \sigma_N=c_N-c_BB^{-1}N\)
\(\sigma_j=c_j-c_BB^{-1}p_j\)
- 非基变量变化:只计算改变的一列即可
- 基变量变化:需要重新计算所有非基变量的检验数
③ \(a_j\) 的变化
\(A'=B^{-1}A \quad p_j'=B^{-1}p_j\)
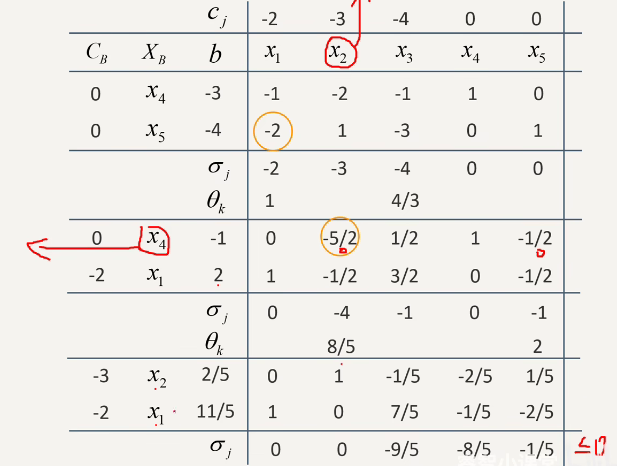
问:如何安排产品产量,可获最大利润?
| 原料 | 产品 | A | B | C | 备用资源 |
|---|---|---|---|---|---|
| 甲 | 1 | 1 | 1 | 1 | 12 |
| 乙 | 1 | 2 | 2 | 2 | 20 |
| 利润 | 5 | 8 | 6 |
解:\(max z=5x_1+8x_2+6x_3\)
\(\begin{cases} x_1+x_2+x_3+x_4=12 \\ x_1+2x_2+2x_3+x_5=20 \\ x_1,x_2,x_3\geq0 \end{cases}\)
最终单纯形表:
| 5 | 8 | 6 | 0 | 0 | |||
|---|---|---|---|---|---|---|---|
| \(c_B\) | 基 | \(b\) | \(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | \(x_5\) |
| 5 | \(x_1\) | 4 | 1 | 0 | 0 | 2 | -1 |
| 8 | \(x_2\) | 8 | 0 | 1 | 1 | -1 | 1 |
| \(\sigma_j\) | 0 | 0 | 0 | -2 | -2 | -3 |
(1) 非基变量系数 \(c_3\) 的改变范围
\(\sigma_3=c_3-c_BB^{-1}p_3\)
\(=c_3-[5 \quad 8]\left[\begin{array}{cc}2 & -1 \\ -1 & 1\end{array}\right]\left[\begin{array}{c}1 \\ 2\end{array}\right]=c_3-8 \leq 0\)
即 \(c_3 \leq 8\)
(2) 基变量系数 \(c_1\) 的改变范围
\(\sigma_A = c - c_BB^{-1}A\)
\(=[c_1,8,6,0,0]-[c_1,8]\left[\begin{array}{ccccc}1 & 0 & 0 & 2 & -1\\ 0 & 1 & 1 & -1 & 1 \end{array}\right]\)
\(=[0,0,-2,-2c_1+8,c_1-8]\leq 0\)
\(\begin{cases} -2c_1+8\leq 0 \\ c_1-8\leq 0 \end{cases} \quad \therefore 4\leq c_1\leq 8\)
保持最优方案不变,求 \(b_1\) 的变化范围。
\(B^{-1}b=\left[\begin{array}{cc}2 & -1 \\ -1 & 1\end{array}\right]\left[\begin{array}{c}b_1 \\ 20\end{array}\right]\geq 0\)
\(\begin{cases} 2b_1-20\geq 0 \\ -b_1+20\geq 0 \end{cases} \quad \therefore 10\leq b_1\leq 20\)

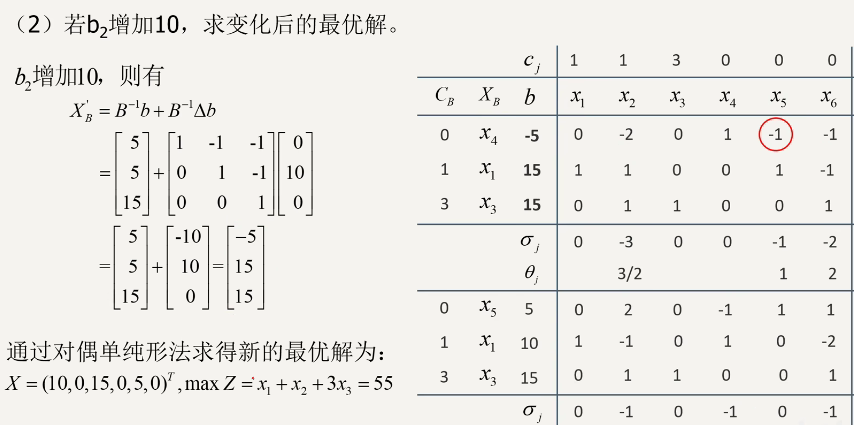
( 计划生产的产品工艺结构改变 )
(1)、非基变量\(x_j\)工艺改变
只影响单纯形表\(p_j\)列,即\(\sigma_j\)。
关键看\(\sigma_j\leq 0\)?还是\(>0\)?可用类似前述方法解决。
(2)、基变量\(x_j\)工艺改变,具体分析
例:对于新产品 D,已知 1 个单位 D 要消耗甲 : 3 乙 : 2
问:保持原有生产比例,利润为多少时,投产产品D有利?
解:\(\sigma_6=c_6-c_BB^{-1}p_6=c_6-[-5 \quad 8]\left[\begin{array}{cc}2 & -1 \\ -1 & 1\end{array}\right]\left[\begin{array}{c}3 \\ 2\end{array}\right]=c_6-12>0\)
得 \(c_6>12\)
例:新增加电力约束:13 已知 A、B、C 每单位需电 2、1、3
问:原方案是否改变?
解:\(2x_1+x_2+3x_3\leq 13\);原方案 A: 4 B: 8 C: 0;\(16>13\) 原方案要改变
例题 ¶
套裁问题¶
注意这种先分情况,再列写方案求解的思路
例:某车间接到制作 100 套钢架的订单,每套钢架要用长为 2.9m,2.1m,1.5m 的圆钢各一根,已知原料长 7.4m,问应如何下料,可使所用原料最省。
| 方案 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 2.9 | 1 | 2 | 0 | 1 | 0 |
| 2.1 | 0 | 0 | 2 | 2 | 1 |
| 1.5 | 3 | 1 | 2 | 0 | 3 |
| 合计 | 7.4 | 7.3 | 7.2 | 7.1 | 6.6 |
| 剩余 | 0 | 0.1 | 0.2 | 0.3 | 0.8 |
设 \(x_j\) 为按方案 \(j\)下料的原料根数
结果 : \(X^*=\left[30, 10, 0, 50, 0\right]^T ,\quad z^*=16m\)
最优跟踪控制问题¶
已知被控对象的输入输出模型为:
\(y(k+1) = 0.5\cdot y(k) + u(k)\quad k = 1,2,\dots,10\)
控制输入约束
\(|u(k| \le M \quad |u(k+1)-u(k)| \le N \quad k = 1,2,\dots,10\)
求使下列目标最小的控制序列 \(u(k)\)
\(\mathop{min}\limits_{u(k),1\le k\le 10} \ max |y(k)-r(k)|\)
令 \(t = max |y(k)-r(k)|\)
\(-t\le y(k+1)-r(k) \le t\)
非线性约束线性化
绝对值变成双向不等式
运输规划 ¶
运输规划是研究如何在满足一定约束条件下,将货物从产地运到销地的最优方案,包括以下内容:
(1)求初始基本可行解——最小元素法、伏格尔法、西北角法
(2)求检验数并判断——闭回路法、位势法
(3)调整运量——闭回路法
产销平衡模型¶
s.t.
其中,\(a_i\) 表示第 \(i\) 种产品的生产量,\(b_j\) 表示第 \(j\) 种产品的销售量。
问题的特点 ¶
-
\(A\) 矩阵稀疏,\(P_{ij}=[0,...,0,1,0,...,0,1,0,...,0]^T\)
-
基变量只有 \(m+n-1\) 个
-
一定存在(有界)最优解,\(x_{ij}=\frac{a_jb_j}{\sum\limits_{i=1}^ma_i}=\frac{a_jb_j}{\sum\limits_{j=1}^nb_j}\) 可行解
为什么基变量是 \(m+n-1\)
数学模型总共有m*n 个变量(m 个产地和 n 个销售地一一组合
又因为这是产销平衡下的运输问题模型,所以产量之和也等于销量之和\(\sum\limits^m_{i=1}a_i = \sum\limits^n_{j=1}b_j\)
也就是说,可以做到有两行完全一样,比如让前面的m行加到其中一行,后面的n行加到其中一行,就会得到两个相同的约束条件,一行减去另一行得到一行全为0的向量。
结合矩阵秩的求法,最小非零行数为矩阵秩的值;所以模型最多只有 m+n-1 个独立约束方程,即系数矩阵的秩 r<=m+n-1.
\(\sigma_j = c_j-c_B \mathbf{B}^{-1}P_j\)
\(\sigma_j = c_j - Y^T P_j\)
基变量检验数为 0
表上作业法:求初始基可行解 ¶
可以使用简化版的单纯形法求最优解 , 该方法称为 " 表上作业法 "
西北角法 ¶
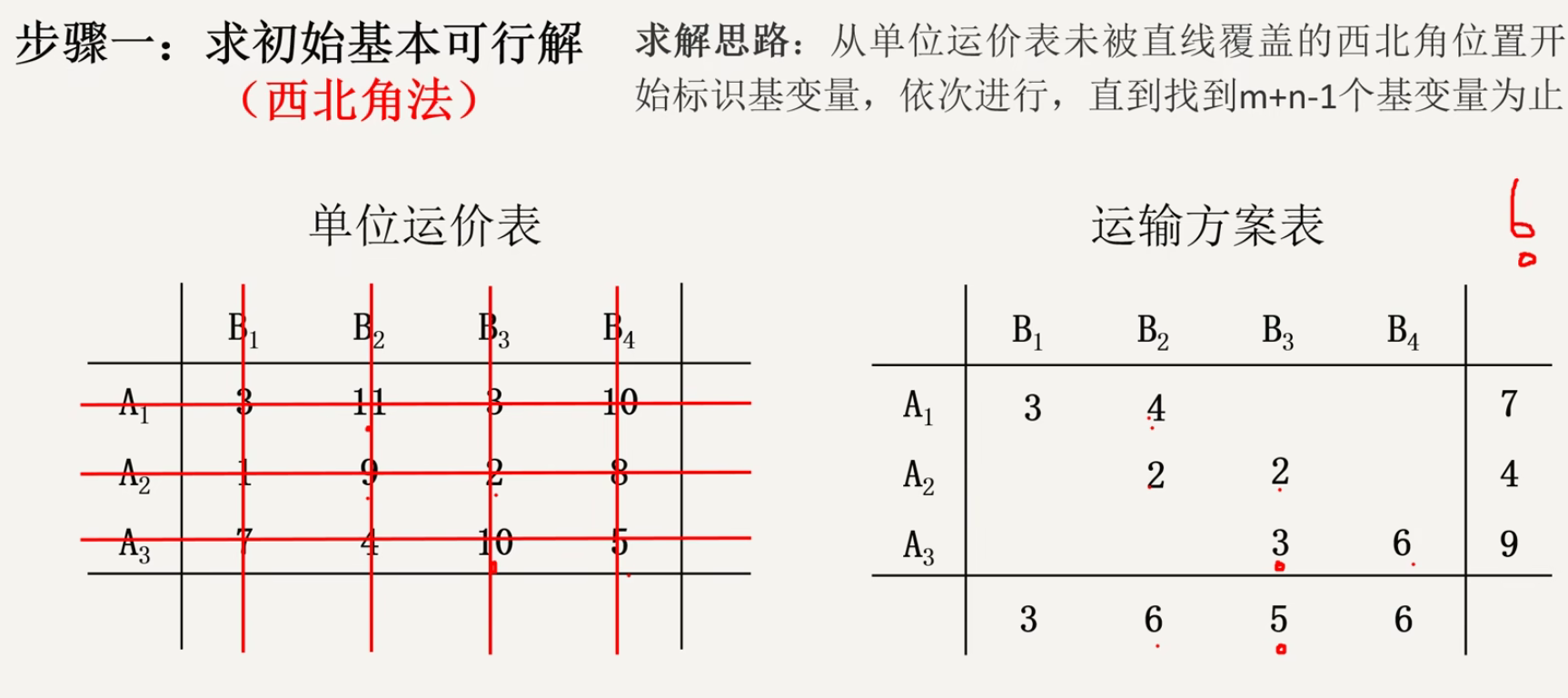
最小元素 ¶
使用贪心的思想,优先安排满运费最低的
就近供应 , 从运费最小的地方开始供应 , 然后逐步供应运费稍高的地方 , 直到最终供应完毕为止 ;
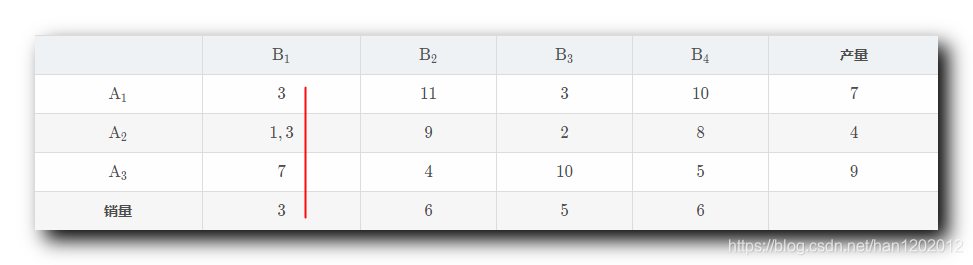
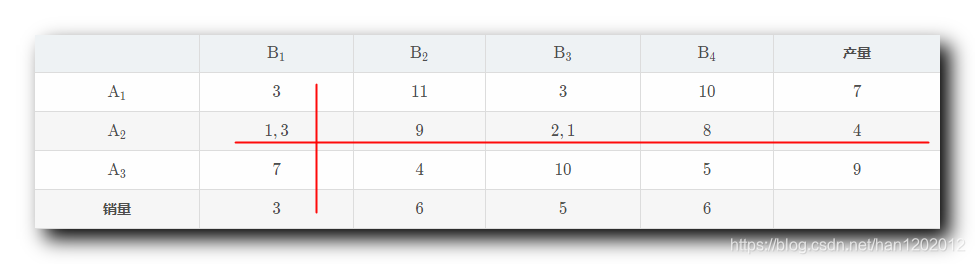
差额法 ( Vogel ) ¶
" Vogel 方法 " 的核心思想就是从运价表中 , 分别计算 各行 , 各列 的 最小运费 和 次最小运费 差额 , 填写到表的 最右列 和 最下行 ;
应该 优先满足差额较高的行列 优先安排运输 ;
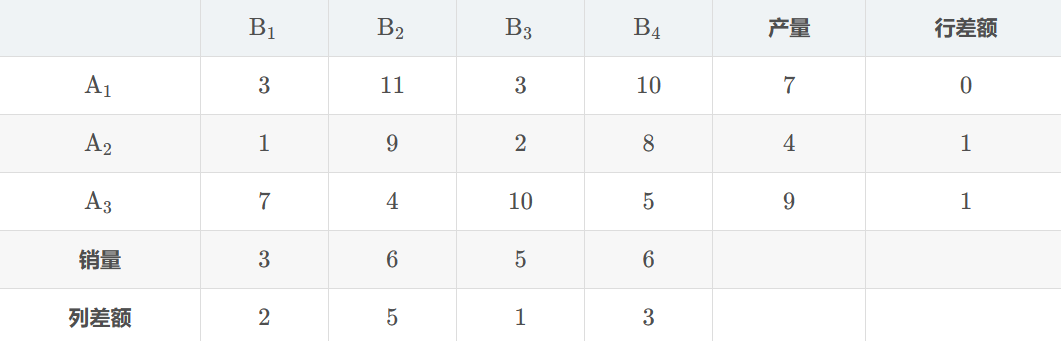
最优性检验 ¶
得到一组基可行解之后,使用检验数判定该解是否是最优解。
检验数符号
变量 \(x_{ij}\) 的检验数记作 \(\lambda_{ij}\)。
检验数判定原则
运输规划的目标函数求最小值时,所有的非基变量检验数 \(\lambda_{ij}\) 都非负,该基可行解就是最优解,该运输方案是最优方案。
求检验数的方法
- 回路法
- 位势法
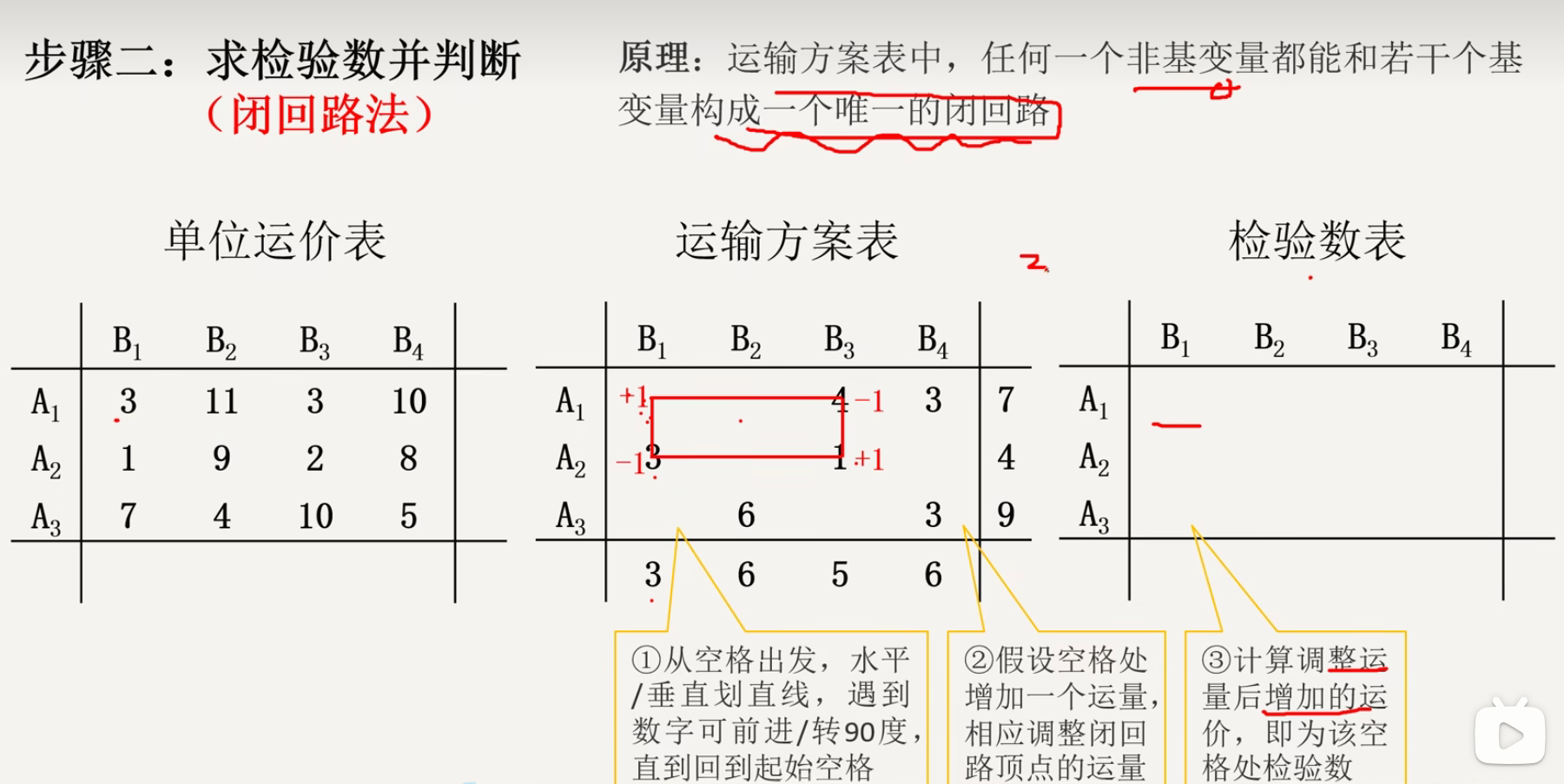
以非基变量为起点 , 出发的格子使用加号 + ++ , 第二个格子使用减号 − -− , 之后的歌词依次使用 加号减号交替 + − +-+− 符号 ;
计算上述闭回路的运费代数和 ,
如果代数和 大于等于 0 , 说明当前的非基变量格子取 0 就是 最优选择 ;
如果代数和 小于 0, 说明当前的非基变量格子取 0 不是最优选择 ;
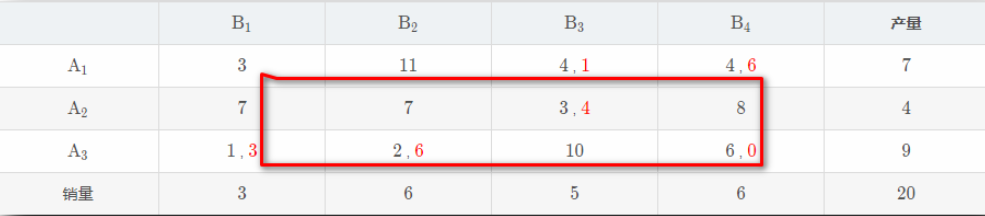
\(\sigma_{11} = 3-1+6-4 = 4\geq 0\)
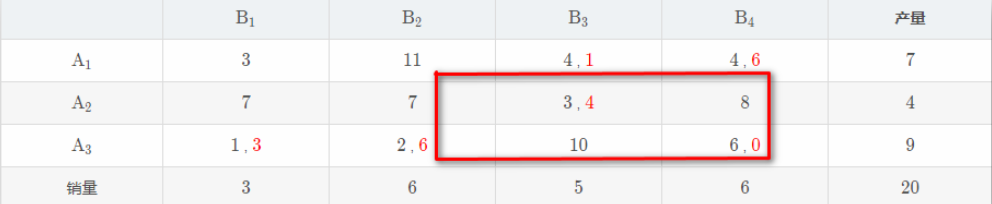
\(σ_{12}=11−2+6−4=11\geq0\)
所有的非基变量检验数都 \(\geq 0\) , 当前的基可行解就是最优解 ;
整数规划 ¶
核心问题
根据整数规划问题的的松弛问题的最优解 , 如何找其整数规划问题 的整数最优解 , 是整数规划问题的核心问题
- 纯整数规划:\(x_j\) 全部取整数的线性规划。
- 混合整数规划:\(x_j\) 部分取整数的线性规划。
- 0-1 型整数规划:\(x_j\) 只能取 0 或 1 的线性规划。
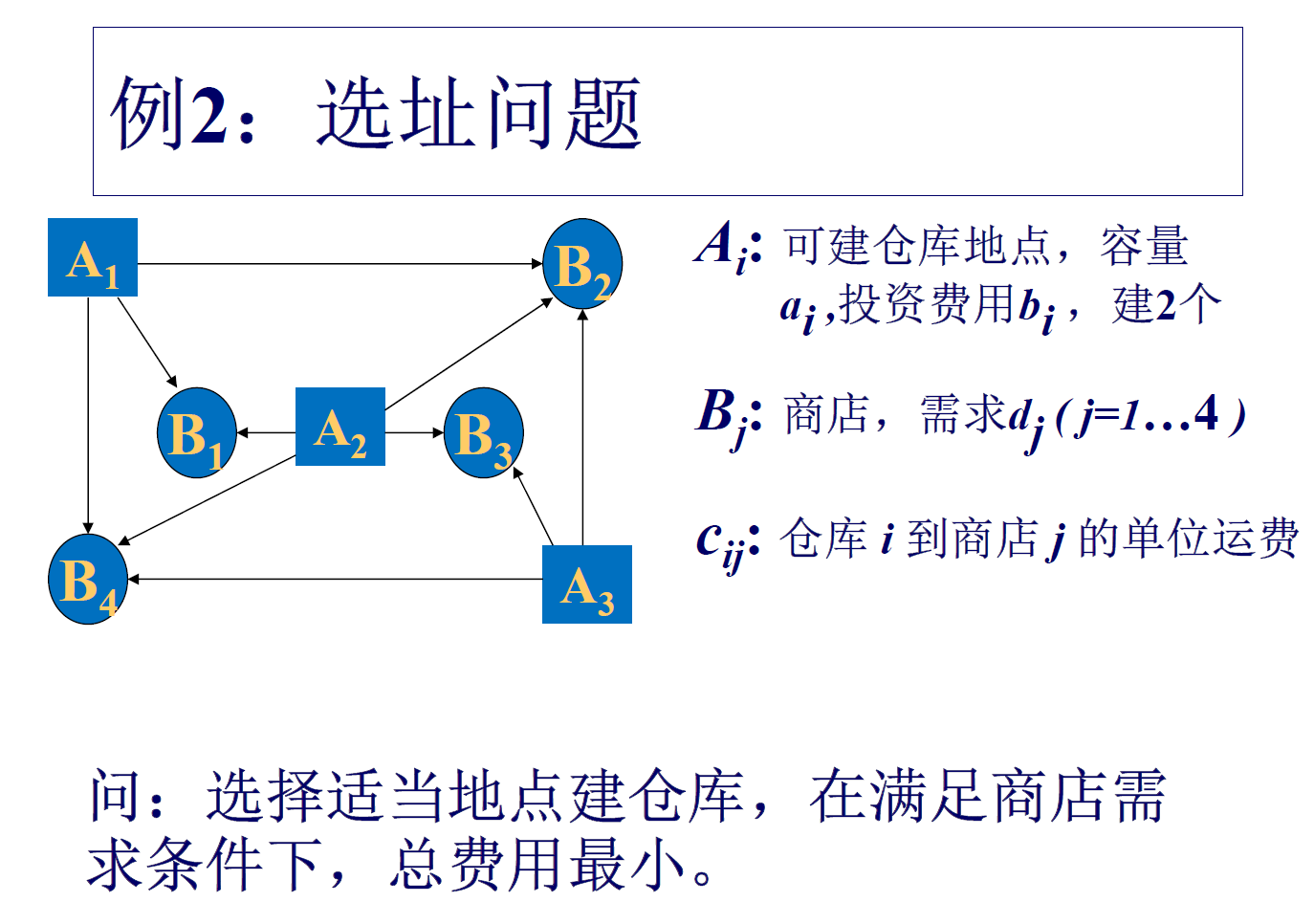
数学模型 ¶
-
如何将第 \(i\) 个变量排除在外:在右侧约束中乘上逻辑变量 \(y_i\)
-
不等式约束如何满足:右侧加上极大数 \(M\),约束变为 \(a_{i1}x_1+a_{i2}x_2+\dots a_{in}x_n \le b_i + M\cdot(1-y_i)\),则 \(y_i = 0\) 时候,约束无效
-
\(p\) 个约束当中只有 \(q\)个有效 \(a_{i1}x_1+a_{i2}x_2+\dots a_{in}x_n \le b_i + M\cdot(1-y_i) \\ y_1 + \dots + y_p = p-q\)
-
前置课程,选 2 必须先选 1 约束:逻辑变量 \(y_1 \ge y_2\)


朴素思想:找松弛最优解周围的整数点;但有可能找不到严格最优解
松弛问题:放松原规划问题的整数条件所得到的新规划问题。
分支定界法 ¶
分治 + 剪枝
分枝:将原问题转化为子问题;
定界:确定界限减少搜索范围。
优点 ¶
(1)、可求解混合整数规划;
(2)、思路简单、灵活;
(3)、速度快;
(4)、适合上机。
步骤 ¶
将每个变量分为上下最接近的两个整数,逐步满足整数规划的约束条件。
- 求松弛问题的最优解
-
分支与定界
任选一个非整数解变量 \(x_i\),在松弛问题中加上约束:
\(x_i \leq \lfloor x_i \rfloor\) 和 \(x_i \geq \lceil x_i \rceil + 1\) -
检查到分支松弛问题的解及目标函数值:
如果该分支的解是整数,并且目标函数值大于等于其它分支的目标值,则剪去其它分支,停止计算;
如果没有得到最优整数解,如果该分支的解是小数,并且目标函数值大于整数解的目标值,需要继续进行分支,直到得到最优解。
新的分支松弛问题特征:
- 原问题求最大值时,目标值是分支问题的上界;
- 原问题求最小值时,目标值是分支问题的下界;
例子 ¶
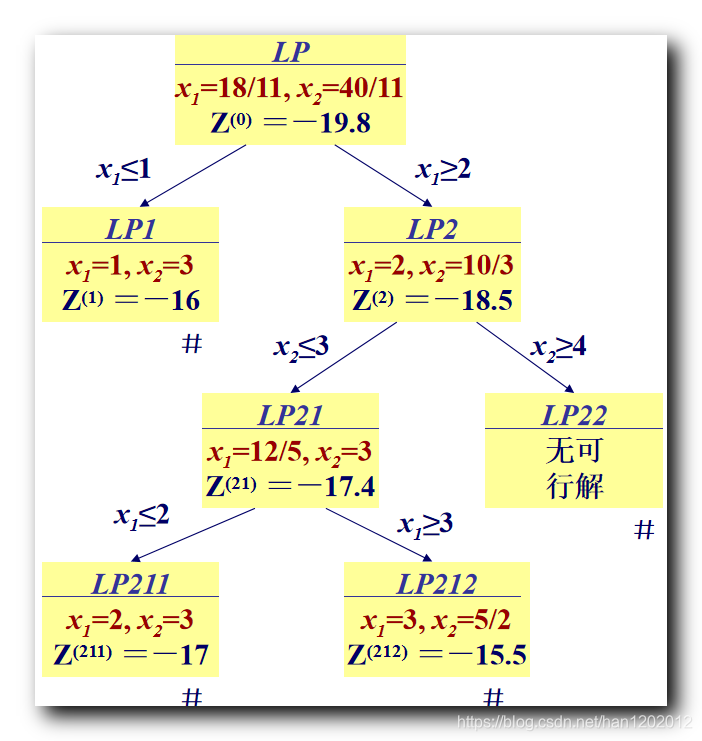
割平面法 ¶
思路:构造切割可行域问题的割平面,把整数 最优解变为切割后松弛问题的顶点。
割一刀,最好使得整数解处于顶点的位置上
利用整数约束条件引入新变量,构造新的松弛问题进行求解。
割平面法解题的标准形式
注意: 当\(a_{ij}\)不是整数时,可乘以某一个倍数化为整数。 目的: 使所有的松弛变量、人工变量均为整数。
(0-1) 指派问题 ¶
s.t.
独立零元素的个数
定理 (D.Konig): 系数矩阵 C 中独立零元素的个数最多等于能覆盖所有零元素的最少直线数。
- 标记没有独立零元素所在行
- 标记打√行中所有非独立零元素所在列
- 标记打√列中独立零元素所在行
- 没有打√的行和打√的列标上直线
克尼格定理
在分配问题中,对于效率矩阵 \([a_{ij}]\),进行以下操作:
- 对每一行元素加上或减去一个常数\(u_i\)。
- 对每一列元素加上或减去一个常数\(v_j\)。
得到新的效率矩阵\([b_{ij}]\),两个效率矩阵\([a_{ij}]\)与\([b_{ij}]\)分配问题的最优解相同。
算法复杂度 \(O(n^4)\)

应用举例 ¶
- 旅行商问题(Traveling Salesman Problem):给定一个包含若干城市的集合,以及两两城市之间的距离,求解访问每个城市一次后回到起始城市的最短路径。这是一个 NPC 问题。
- 生产调度问题(Production Scheduling Problem):给定一组工作任务和它们的时序约束,确定一个可行的生产调度计划。这个问题是 NP-hard 的。
- 0-1 背包问题(Knapsack Problem):给定一组物品和它们的重量、价值,以及一个背包的容量限制,求解如何选择物品以最大化背包中的总价值。这是一个 NP-hard 问题。
- 装箱问题(Bin Packing Problem):给定一组物品和它们的尺寸,以及一些相同尺寸的箱子,求解如何将物品装入箱子以最小化使用的箱子数量。这是一个 NPC 问题。
- 图着色问题(Graph Coloring Problem):给定一个图和一些颜色,求解如何为图中的每个顶点分配颜色,使得没有两个相邻的顶点有相同的颜色。这是一个 NPC 问题。
- 聚类问题(Clustering Problem):给定一组数据点和它们的相似性度量,求解如何将它们分成不同的聚类,使得相似的点在同一聚类中,而不相似的点在不同聚类中。这个问题是 NP-hard 的。
目标规划 ¶
思想:软约束 + 优先级
概念与定义 ¶
目标规划是用来解决多目标规划问题的,并且决策者事先对每个不同的目标都存在着一个期望值即理想值;即通过之前的生产运营数据计算出的最优值
-
多个约束,很可能可行域为空 \(\rightarrow\) 为约束设置不同的优先级,先满足高优先级的约束
-
常常存在多目标:分清主次,设置优先级(d 的编号越小,优先级越高
) ,并按照优先级进行加权,构成一个新的单目标函数 - 保证多个目标尽可能接近,而不会放弃某个目标
硬约束与软约束
- 硬约束:指必须严格满足的等式约束和不等式约束。这些约束是由客观条件限定的,一定要满足的,管理者无法控制,故不应考虑其偏差变量。
- 软约束:实现起来可以有偏差(di)的管理目标约束。实际中不要求绝对满足,所求解不一定是可行解,但是是满意解
偏差变量 \(d_i\):表示实际值与目标值之间的差距。
-
$d_i^+ $ 正偏差,表示实际值 - 指标值
-
\(d_i^-\)负偏差,表示指标值 - 实际值
与线性规划区别
- 线性规划的目标是一个刚性的目标 . 但实际应用中,目标常常是模糊的;解决方法:建立软约束
- 线性规划立足于求满足所有约束条件的可行解,要求各个约束条件相容且可行域不是空集,而实际中的问题往往存在相互矛盾的约束条件 , 目标规划可在相互矛盾的约束条件下找到满意解 , 即满意方案 .
- 线性规划只能处理一个目标的问题 , 而目标规划能够统筹兼顾多个目标的关系求得更切合实际的解 .解决方案:设置优先级
- 目标规划找到的最优解是指尽可能达到或接近一个或多个已给定指标值的满意解
- 线性规划对约束条件是不分主次地同等对待 , 而目标规划可根据实际需要给予轻重缓急的考虑 .
建模 ¶
\(\max d^+\) 与 \(\min d^-\) 的选择
| 条件 | 结果 |
|---|---|
| \(f(x) = g\), 恰好达到目标值 | \(\min z = f(d^+_k + d_k^-)\) |
| \(f(x) \ge g\),超过指标值,正偏差不限制,负偏差尽量小 | \(\min z = f(d_k^-)\) |
| \(f(x) \le g\),不超过指标值,负偏差不限制,正偏差尽量小 | \(\min z = f(d_k^+)\) |
| 当实际值确定只会大于目标值时 | \(d_i^+>0\),而 \(d_i^-=0\) |
| 当实际值确定只会小于目标值时 | \(d_i^->0\),而 \(d_i^+=0\)。 |
| 实际值等于目标值时 | \(d_i^+=d_i^-=0\) |
| 任何一种情况 | \(d^+ \cdot d^- = 0\) |
优先因子 \(P\)¶
绝对优先级
- \(\min\{P_1d_1^+,P_2d_2^+\}\)
- \(\alpha_1 \gg \alpha_2 \gg \alpha_3\)
相对优先级
- 调整同一绝对优先级下的相对优先级
单纯形法求解 ¶
使用单纯形法求解 \(d^+ \cdot d^- = 0\) 自动满足
\(d^+\) 和 \(d^-\) 不可能同时是基变量;无论怎么变换,都是相反数的关系
序贯法求解 ¶
有 K 个优先级,先按照第一个优先级求得最优值
将已计算目标函数值,作为下一级目标的硬约束。
再求第二优先级的最优值