跳转至

第四章 Tree

约 1090 个字 预计阅读时间 4 分钟

术语解释

树是 N 个节点和 N-1 条边的集合

节点 \(n_i\) 的深度为从根到 ni 的唯一路径的长

节点 \(n_i\) 的高度为从 ni 到一片树叶的最长路径的长

树的高度等于根的高度

性质

  • 无环
  • 加上一条边就有环，去掉一条边就不连通
  • 节点数 = 所有节点的度数 +1
  • 度为 m 的树，第 i 层至多有 \(m^{i-1}\) 个节点
  • 最多节点：（等比数列求和）\(\frac{m^h - 1}{m-1}\)
  • n 个结点的 m 叉树最小高度 代入上一行

1、先序遍历：先遍历根节点，再遍历左节点，最后遍历右节点； 2、中序遍历：先遍历左节点，再遍历根节点，最后遍历右节点； 3、后序遍历：先遍历左节点，再遍历右节点，最后遍历根节点；

二叉树

特点：

每个节点都不能有多于两个的儿子

实现：

image-20230101184951393

二叉查找树BST binary search tree

特点：

对于树中的每一个节点 X，它的左子树中所有项的值都小于 X 中的项，它的右子树中所有项的值都大于 X 中的项。

contains

思路：遇到比 X 小的节点就递归右子树；遇到比 X 大的节点就递归左子树

image-20230101190630001

findMin 和 findMax

思路：一直往左走或者一直往右走

image-20230101190756266

insert

思路：像 contains 一样沿着树查找，如果找到 X 则什么也不做，否则将 X 插入到所遍历路径的最后一点上。

image-20230101191356007

remove

思路：

如果节点是树叶，直接删除

如果节点有一个儿子，则该节点的父节点调整它的链以绕过该节点后删除

如果节点有两个儿子，用其右子树的最小数据代替该节点的数据并且递归删除那个节点

image-20230101192614904

AVL 树

结点数目一定，保持树的左右两端保持平衡，树的查找效率最高。

用插入的成本弥补查询的效率

但当插入操作多于查询操作时候不方便。

特点：

带有平衡条件的二叉搜索树，它保证树的深度是 O(log(N))，平衡条件为其每个节点的左子树和右子树的高度最多相差 1的二叉查找树。每个节点都保留高度信息。

方法：

问题结构：左右深度差值 >1

从第一个有问题的节点开始，向叶子节点伸展三个节点，把中间数字第二大的节点提升，其他两个节点分列两侧——左边放左边，右边放右边。

image-20231113142105049

image-20231113142031094

image-20230101195437730

1 和 4 使用单旋转 2 和 3 使用双旋转

单旋转

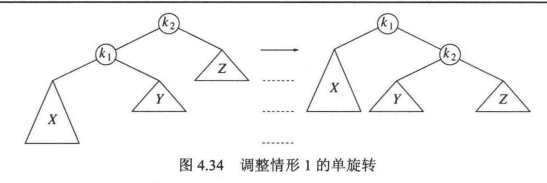
image-20230101200041908

思路：将 X 上移一层，Z 下移一层，抓住 k1 轻轻抖动

双旋转

旋转前条件：

深度高的是左子树，那么左子树平衡必须偏左，如果偏右，则需要加一次旋转使得平衡偏左，最后再右转；

深度高的是右子树，那么右子树平衡必须偏右，如果偏左，则需要加一次旋转使得平衡偏右，最后再左转；

image-20230101202411868

image-20230101202422717

balance

image-20230101202654097

image-20230101202711279

红黑树

特点

最长子树不超过最短子树的 2 倍

不需要很多旋转

方法

  1. 根节点是黑色的
  2. 插入节点是红色的
  3. 看叔叔脸色（叔叔红脸，三世取反；叔叔黑脸，AVL 调整）

缺点

树的深度变多，查找次数增加，io 变慢

红黑树不严格要求平衡，且再插入、排序、查询操作时候更为稳定。

在连续插入操作时，效率较高。

红黑树的插入实现

什么是红黑树动画理解

伸展树

应用：输入法候选框，cache

一个节点在一次被访问后，这个节点很可能不久再次被访问。那么伸展树的做法就是在每次一个节点被访问后，我们就把它推到树根的位置。

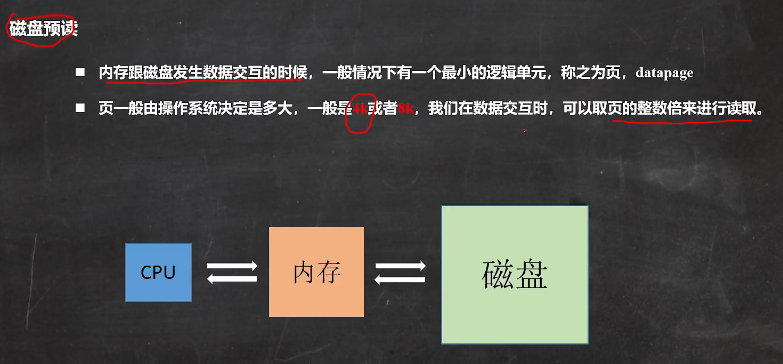
B-tree

key-value 文件系统的索引

线性表和哈希表不合适

b 树的引用

有序的多路平衡查找树

绝对平衡 每一个节点高度都相同，平衡因子均等于 0

image-20231113153948020

image-20231113154712384

B+tree

非叶子节点只存储记录，叶子节点存储数据。

把空间让渡给索引