第七章 Sorting ¶
约 480 个字 158 行代码 预计阅读时间 4 分钟
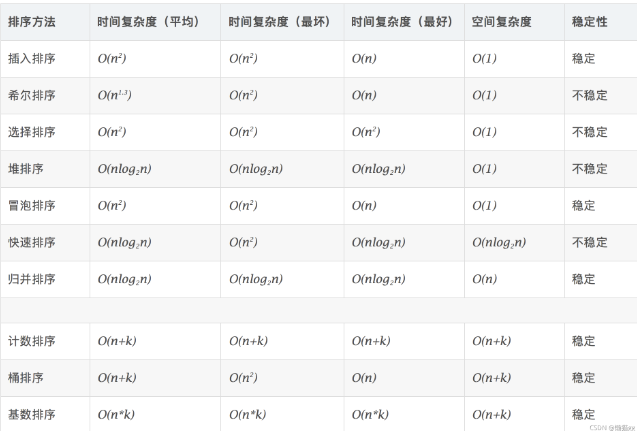
n2 级 ¶
冒泡排序 ¶
// bubble sort
std::vector<int> bubble_sort(const std::vector<int> &arr){
std::vector<int> sorted_array = arr;
int n = sorted_array.size();
for(int i = 0; i < n; i++)
for(int j = i+1; j < n;j++)
if(sorted_array[i] > sorted_array[j])
std::swap(sorted_array[i],sorted_array[j]);
return sorted_array;
}
选择排序 ¶
// selection sort
std::vector<int> selection_sort(const std::vector<int> &arr){
std::vector<int>sorted_array = arr;
int n = sorted_array.size();
for(int i = 0; i < n;i++){
int min = sorted_array[i];
int s = i;
for(int j = i; j < n; j ++){
if(sorted_array[j] < min)
s = j;
}
std::swap(sorted_array[i],sorted_array[s]);
}
return sorted_array;
}
插入排序 ¶
在第 p 趟,将位置 p 上的元素向左移动直至找到它在前 p+1 个元素中的正确位置
时间复杂度 O(N^2)
N 个互异的元素的数组的平均逆序数是 N(N-1)/4
通过交换相邻元素进行排序的任何算法时间复杂度 Ω(N^2)
// insertion sort
std::vector<int> insertion_sort(const std::vector<int> &arr){
std::vector<int> sorted_array = arr;
int n = sorted_array.size();
for(int i = 1; i < n ;i++){
int j = i-1;
int key = sorted_array[i];
while(j > 0 && key < sorted_array[j]){
sorted_array[j+1] = sorted_array[j];
j--;
}
sorted_array[j+1] = key;
//注意这里的写法,省略了一些步骤,不管j是否移动过,这样都可以保证最后插入正确
}
return sorted_array;
}
希尔排序 ¶
//shell_sort
std::vector<int> shell_sort(const std::vector<int> &arr){
std::vector<int> sorted_array = arr;
int n = sorted_array.size();
for(int gap = n>>1; gap > 0; gap >>=1){
for(int i = gap; i < n;i++){
int key = sorted_array[i];
int j = i-gap;//注意这里起始的位置
while(j > 0 && sorted_array[j] > key){
sorted_array[j+gap] = sorted_array[j];
j-= gap;
}
sorted_array[j+gap] = key;
}
}
return sorted_array;
}
nlogn 级 ¶
快速排序 ¶
(1) 如果 S 的元素个数为 0 或 1 返回
(2) 取 S 中的一个元素 v 为枢纽元
(3) 将 S-v 划分成两个不相交的集合
(4) 返回 {qiucksort(S1),v,qiucksort(S2)}
可以三个元素去中间值来确定枢纽元以及小数组直接快速排序
快速排序最慢 O(N^2) 平均 sita(NlogN)最坏 O(NlogN)
// quick sort
int partition(std::vector<int> &arr,int left,int right){
int pivot = arr[left];
int i = left+1,j = right;
while(i <= j){
while(i<=j && arr[i] < pivot) i++;
while(i<=j && arr[j] > pivot) j--;
if(i <= j) std::swap(arr[i++],arr[j--]);
}
std::swap(arr[left],arr[j]);
return j;
}
void quick_sort(std::vector<int> &arr,int left,int right){
if(left < right){
int pivot_position = partition(arr,left,right);
quick_sort(arr,left,pivot_position-1);
quick_sort(arr,pivot_position+1,right);
}
}
归并排序 ¶
将数组分而治之,最后再加上线性的 O(N) 合并的代价
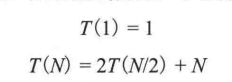


// merge sort
void merge(std::vector<int> &arr,int left, int mid , int right ){
std::vector<int> temp(right-left+1);//这里一定要初始化长度
int i = left, j = mid + 1, k = 0;
while(i <= mid && j <= right){
temp[k++] = arr[i]<arr[j]? arr[i++]:arr[j++];
}
while(i <= mid) temp[k++] = arr[i++];
while(j <= right) temp[k++] = arr[j++];
for(int i = 0; i < k;i++){
arr[left+i] = temp[i];
}
}
void merge_sort(std::vector<int> &arr,int left,int right){
if(left < right){
int mid = (left + right)/2;
merge_sort(arr,left,mid);
merge_sort(arr,mid+1,right);
merge(arr,left,mid,right);
}
}
堆排序 ¶
建立 N 个元素的二叉堆 O(N)
执行 N 次 deleteMin 每次 O(logN)
总运行时间 O(NlogN)
// heap sort
void heapify(std::vector<int> &arr, int n, int i ){
//在长度为n的二叉堆中调整第i个元素
int max = i;
int left = 2*i +1, right = 2*i + 2;
if(left < n && arr[left] > arr[max]) max = left;//这里一定要写left<n的判断,不然不会是你想要排序的序列
if(right <n && arr[right] > arr[max]) max = right;
if(max != i){
std::swap(arr[max],arr[i]);
heapify(arr,n,max);
}
}
void heap_sort(std::vector<int> &arr){
int n = arr.size();
//构建最大堆,从倒数第二层开始调整
for(int i = n/2-1; i >=0;i--){
heapify(arr,n,i);
}
//查询堆顶元素并调整到数组末尾
for(int i = n-1 ; i >0 ;i--){
std::swap(arr[0],arr[i]);
heapify(arr,i,0);
}
}
其他 ¶
桶排序 ¶
桶排序(Bucket sort)是将数据分到有限数量的桶子里,然后每个桶再分别排序
先创建 n 个桶,桶的区间跨度 =( 最大值 - 最小值 )/ 桶的数量
遍历原始序列,将序列放入桶中
每个桶内部的元素分别排序
遍历所有桶,将桶中元素依次输出
O(M+N)
计数排序 ¶
稳定性:保持顺序不变
void counting_sort(vector<int> &arr,int exp){
const int n = arr.size();
const int base = 10;//基数排序10进制
vector<int> counting_array(base);
for(int i = 0; i < n;i++){//注意这里是循环原数组
counting_array[(arr[i]/exp)%base]++;
}
//计算前缀和
vector<int> prefix_sum_array(base);
prefix_sum_array[0] = counting_array[0];
for(int i = 1;i < base;i++){
prefix_sum_array[i] = prefix_sum_array[i-1] + counting_array[i];
}
//排序
vector<int> sorted_array(n);
for(int i = 0; i < n;i++){
int index = prefix_sum_array[(arr[i]/exp)%base] - 1;
sorted_array[index] = arr[i];
prefix_sum_array[(arr[i]/exp)%base]--;
}
for(int i = 0; i < n ;i++){
arr[i] = sorted_array[i];
}
}
基数排序 ¶
基数排序(Radix Sort)是将待排序序列的每个元素统一为同样位数长度的元素,位数较短的通过补 0 达到长度一致,然后从最低位或从最高位开始,依次进行稳定的计数排序,最终形成有序的序列
对于每一位进行计数排序,从而达到
穿孔制表机