第五章 散列表与 hash ¶
约 1361 个字 预计阅读时间 5 分钟
address = H [key]
找不同 找相同 经典的 hash 应用
散列表 ¶
一种以常数平均时间执行插入删除查找的技术
根据关键码值 (Key value) 而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
冲突:
当一个元素被插入时与一个已经插入的元素散列到相同的值
分离链 ¶
接法 ¶
将散列到同一个值的所有元素保存到一个链表中
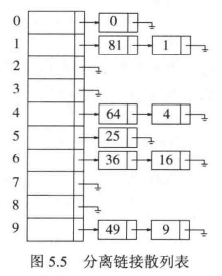
装填因子:散列表中的元素个数 / 该表的大小 等于链表的平均长度
填装因子越低,发生冲突的可能性越小,散列表的性能越高。一旦填装因子大于 1,就应该调整散列表的长度。
线性探测法 ¶
遇到冲突后,就按照某种规则,寻找下一个位置,直到找到空位置为止;
线性探测就是在发生冲突后,在原来的地址上往下一个地址找,一个一个的往下探测,直到找到空位置为止。
容易出现一次聚集 适用于装填因子小于 0.5
平方探测法 ¶
平方探测就是在发生冲突后,在原来的地址上往下(\(1^2, 2^2\)…)地址找,一个一个的往下探测,直到找到空位置为止。
解决一次聚集问题 快速
双散列 ¶
hash1 = x mod m
小于 n 的质数 z
hash2 = z - (x mod z)
冲突函数: f(i) = i * hash2(x)
耗时间 预期探测次数几乎和随机冲突解决方法的情形相同
再散列 ¶
对于使用平方探测的开放定址散列法,如果散列表填的太满,那么操作的运行时间将开始消耗过长,且插入操作可能失败。一种解决方法是建立另外一个大约两倍大的表,扫描整个原始散列列表,计算每个(未删除的)元素的新增散列值将其出入新表中,这个操作就是再散列。
散列表何时扩展,大多数实现是设置一个装载因子 α(设 m 和 n 分别表示表长和填入的点数,则将 α = n/m 定义为散列表的装填因子,α 越大,表越满,冲突越大
删除方法 ¶
- 永不删除
- 标记法
伪随机数 ¶
独立
均匀 同余方法保证
简单均匀哈希 simple uniform hashing
\(P(h(k) = i) = \frac{1}{m}\)
\(E[T] = (1+\Theta(\frac{n}{m})),\alpha := \frac{n}{m}\) 为装载率
乘同余方法 ¶

MT19937¶
全域散列解决的是确定性散列算法无法应对特殊输入的问题。我们有 m(为方便讨论,不妨设 m 远大于 2)个格子时,单个好的散列函数的冲突概率是 1/m(已经均匀散列了,但还会恰好两个掉到同一个格子里
灵感是随机地选散列函数。如果散列函数是随机选择的,那么精心构造的数据就不一定起作用了。但是,
- 多少个备选函数才够呢?比如,两个是不够的。比如我们有两个散列函数 h1 和 h2 来随机选择,各 50% 概率被选到。那么构造一个 h1 的特殊输入(让 h1 100% 冲突
) ,这个输入里任意两个元素仍然会有 50% 的情况一定冲突(就是 h1 被选中的概率) ,没有达到理想的 1/m。 - 备选函数够多就可以吗?比如,这些函数都会在两个特殊的点上面冲突,即存在 x != y,使得任取 h 都有 h(x) == h(y),那么用这两个点作为输入,冲突概率就是 100%。也就是说,这些函数冲突的地方还不能太重合。
全域散列指出可以选择 |H| 个散列函数,且它们最大重合 ≤ |H|/m。其中重合是指,对任意 x != y,散列函数集合 H 中 h(x) == h(y) 的散列函数个数。随机选择散列函数后,对于精心构造的 x, y(我知道 x, y 会在某个或某些函数上冲突
hash 的应用 ¶
开发应用一:安全加密 ¶
说到哈希算法的应用,最先想到的应该就是安全加密。最常用于加密的哈希算法是 MD5(MD5 Message-Digest Algorithm,MD5 消息摘要算法)和 SHA(Secure Hash Algorithm,安全散列算法)
开发应用二:唯一标识 ¶
哈希算法可以对大数据做信息摘要,通过一个较短的二进制编码来 表示很大的数据