有趣问题探究 ¶
约 783 个字 预计阅读时间 3 分钟
排队延时问题 ¶
本书作者制作的排队延时的可视化动画
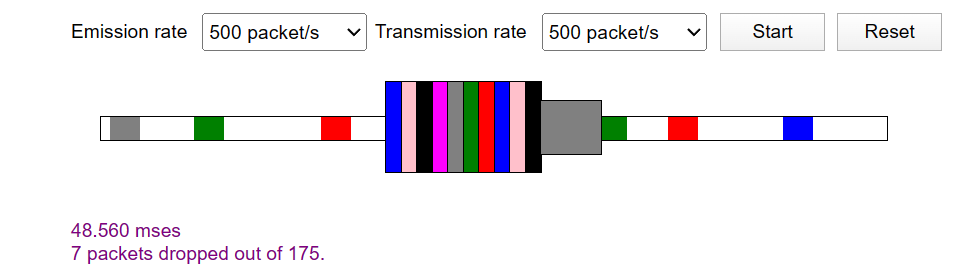
\(\frac{L \cdot a}{R} > 1\)时 ¶
队伍显然越来越长,直到发散
\(\frac{L \cdot a}{R} = 1\) 时 ¶
分为几种情况
- 周期性到达,很规律,来一个发一个,这个时候没有排队延时
类似流水线
- 短时间集中,但是也是规律的;这个时候排队延时是等差数列,平均一下即可
类似车队下高速
- 随机到达,书中只描述了一个趋势:
即趋于 0 的时候排队延时也趋于 0,流量强度趋于 1 时候,排队延时趋于正无穷。
但是也没有说具体数学模型

查询资料 ¶
网上资料假设了两个前提
- 到来分组符合泊松分布
在给定间隔内期望有 \(λ\) 个事件的泊松分布下,同一间隔内 \(k\) 个事件的概率为
\(\frac{\lambda^k e^{-\lambda}}{k!}\)
- 分组等长
证明:在这些假设前提下,流量强度 =1 时候,排队延迟无限大
Denote 到达率为 \(l\),处理速率为 \(u\),也就是该条链路的带宽,流量强度 \(p=\frac{l}{u}\)
考虑到处理单个等长的数据包的时间应该是固定的,根据排队论的知识和 Kendall 表示法,符合 M/D/1 模型,进而由公式得到
平均分组数量 \(Ls=p + \frac{1}{2} \cdot \frac{p^2}{(1-p)}\) 平均排队延时 \(Wq=\frac{p}{2u(1-p)}\)
可以看到 p 趋向于 1 时分母为 0,排队延时趋于无穷。
ref¶
为什么流量强度为 1 时排队时延是无穷? - 知乎 (zhihu.com)

DNS 的过程 ¶
禁用 IP 访问 ¶
不同的域名通过 A 记录或者 CNAME 方式可以连接都同一个 IP 下,同一个 IP 也可以设置多个不同站点,那么访问不同的域名都转发到同一 IP ,怎么区分这些不同的站点呢,就是用的 Host 字段。这样每次访问都会根据不同的 Host 的信息请求到不同的站点上面。
1.host 字段可以是域名,也可以是 ip 地址。host 字段域名 /ip 后可以跟端口号,如 Host: www.6san.com:8080
2.host 可以由程序自定义,某些程序为了防止运营商或防火墙拦截会定义虚假 host
3.http1.1 中 host 字段可以是空值,http1.0 中可以缺失 host 字段
4.http 响应头中不包含 host 字段,所以 wireshark 中 http.host 过滤到的都是请求包
5. 因为 http 头中的 host 字段可以由程序自定义,所以 host 字段的值就会有很多特殊情况,如包含多个’/' 字符的 HOST 头信息,结尾含有”.”等
http 头中可以没有 host 字段吗?
在 http 1.1 中不能缺失 host 字段 , 如果缺失 , 服务器返回 400 bad request,http1.1 中不能缺失 host 字段,但 host 字段可以是空值。
在 http 1.0 中可以缺失 host 字段。