Logic¶
约 3545 个字 预计阅读时间 14 分钟
演绎逻辑的核心逻辑
必然地导出
大部分人都是归纳鬼才、类比高手、演绎残废
基础知识 ¶
- 概念:有意义的词项;ex:苹果、人、桌子
- 命题:概念集合,确定关系;ex:苹果是水果,人是动物,桌子是家具
- 推理:从前提必然地导出结论
- 逻辑:确保推理与论证有效的规则
- 论证:有推出关系的语群

AEIO

逻辑是形式科学,形式有效不等于内容有效
历史 ¶
1. 古代逻辑(公元前 5 世纪–公元 5 世纪)¶
- 苏格拉底、柏拉图与亚里士多德:古希腊哲学家为逻辑学奠定了基础。尤其是亚里士多德,他被认为是逻辑学的奠基人。亚里士多德的《工具论》是逻辑学的经典之作,他提出了“三段论”作为推理的一种形式,这是传统形式逻辑的核心。 - 智者学派:智者学派的成员,如普罗塔戈拉斯,发展了论证技巧和修辞学,影响了后来的逻辑思考,尤其是在推理和辩论的层面。
2. 中世纪逻辑(公元 5 世纪–14 世纪)¶
- 基督教哲学家的影响:在中世纪,逻辑学的研究与神学、哲学紧密结合,特别是亚里士多德的逻辑学被基督教哲学家如托马斯 · 阿奎那等人所采纳并进一步发展。 - 修辞学与辩证法:中世纪的学者不仅关注推理的形式,也研究了语言和修辞如何影响论证的有效性,尤其在辩证法和神学辩论中尤为重要。
3. 近代逻辑的奠基(16 世纪–19 世纪)¶
- 笛卡尔与莱布尼茨:笛卡尔强调数学与理性推理的基础,而莱布尼茨则提出了“理性语言”的概念,预示着后来的符号逻辑的发展。
- 波尔布朗与布尔:乔治 · 布尔在 19 世纪中期发展了代数逻辑(布尔代数
4. 现代逻辑(20 世纪至今)¶
- 符号逻辑与数理逻辑的兴起:20 世纪初,逻辑学经历了深刻的变革,尤其是在哥德尔、不完全性定理、罗素和怀特海的《数理逻辑原理》以及康托尔集合论的影响下。数学逻辑成为一门独立的学科,深入探讨了集合论、命题逻辑、谓词逻辑等基础。 - 形式化与自动化:随着计算机科学的发展,逻辑学的符号化与形式化理论得到了广泛应用。形式化逻辑成为计算机程序设计和人工智能的理论基础。 - 非经典逻辑:20 世纪中期以后,随着对经典逻辑的深刻理解,非经典逻辑如模态逻辑、直觉主义逻辑、直觉主义逻辑等得到了研究。这些逻辑系统挑战了传统逻辑的某些假设,提出了更为多元和灵活的推理方式。
5. 当代逻辑学的发展¶
- 人工智能与自动推理:在现代人工智能的研究中,逻辑学扮演了重要的角色,尤其是在推理、知识表示和自动定理证明等方面。 - 量子逻辑:量子力学的发展导致了量子逻辑的提出,这种逻辑挑战了经典逻辑中的某些基本假设,尤其是关于命题的真值和推理的规则。
词项逻辑:关注概念 ¶
三段论 ¶
思维中澄清概念关系; - 中项必须在前提中周延至少一次
命题逻辑:关注命题——算算算 ¶
命题逻辑是应用一套形式化的规则对以符号表示的描述性陈述进行推理的系统。
命题连接词 ¶
复合命题:穷尽所有符合命题的判断规则
| 命题连接符号 | 表示形式 | 意义 |
|---|---|---|
| 与 (and) | \(p \land q\) | 命题合取 (conjunction),即“p 且 q” |
| 或 (or) | \(p \lor q\) | 命题析取 (disjunction),即“p 或 q” |
| 非 (not) | \(\neg p\) | 命题否定 (negation),即“非 p” |
| 条件 (conditional) | \(p \rightarrow q\) | 命题蕴含 (implication),即“如果 p 则 q” |
| 双向条件 (bi-conditional) | \(p \leftrightarrow q\) | 命题双向蕴含 (bi-implication),即“p 当且仅当 q” |
可以通过真值表判断真假
| \(p\) | \(q\) | \(\neg p\) | \(p \land q\) | \(p \lor q\) | \(p \rightarrow q\) | \(p \leftrightarrow q\) |
|---|---|---|---|---|---|---|
| False | False | True | False | False | True | True |
| False | True | True | False | True | True | False |
| True | False | False | False | True | False | False |
| True | True | False | True | True | True | True |
- 否定 (\(\neg p\)): 当 \(p\) 为假时,\(\neg p\) 为真;当 \(p\) 为真时,\(\neg p\) 为假。
- 合取 (\(p \land q\)): 当 \(p\) 和 \(q\) 都为真时,\(p \land q\) 为真;否则为假。
- 析取 (\(p \lor q\)): 当 \(p\) 或 \(q\) 至少有一个为真时,\(p \lor q\) 为真;否则为假。
- 蕴含 (\(p \rightarrow q\)): 当 \(p\) 为真且 \(q\) 为假时,\(p \rightarrow q\) 为假;否则为真。
- 双向蕴含 (\(p \leftrightarrow q\)): 当 \(p\) 和 \(q\) 都为真或都为假时,\(p \leftrightarrow q\) 为真;否则为假。
蕴含
如果 \(p\) 那么 \(q\):\(p \rightarrow q\),\(p\) 是 \(q\) 的充分条件 , 表示的是一种蕴含关系。所以当 \(p\) 不成立的时候,相当于 \(p\) 是空集,空集是任何集合的子集,所以 \(p \rightarrow q\) 一定成立。
命题演算 ¶
可以使用与或非表示所有命题连接词
通过逻辑等价,我们可以将命题等价地转换为其他命题
| 公式 | 等价公式 |
|---|---|
| \(\alpha \land \beta \equiv \beta \land \alpha\) ( \(\land\) 的交互律 ) | \((\alpha \Rightarrow \beta) \equiv \neg \alpha \lor \beta\) ( 蕴涵消除 ) |
| \(\alpha \lor \beta \equiv \beta \lor \alpha\) ( \(\lor\) 的交互律 ) | \((\alpha \Leftrightarrow \beta) \equiv (\alpha \Rightarrow \beta) \land (\beta \Rightarrow \alpha)\) ( 双向消除 ) |
| \((\alpha \land \beta) \land \gamma \equiv \alpha \land (\beta \land \gamma)\) ( \(\land\) 的结合律 ) | \(\neg (\alpha \land \beta) \equiv (\neg \alpha \lor \neg \beta)\) ( De Morgan ) |
| \((\alpha \lor \beta) \lor \gamma \equiv \alpha \lor (\beta \lor \gamma)\) ( \(\lor\) 的结合律 ) | \(\neg (\alpha \lor \beta) \equiv (\neg \alpha \land \neg \beta)\) ( De Morgan ) |
| \(\neg (\neg \alpha) \equiv \alpha\) ( 双重否定 ) | \((\alpha \land (\beta \lor \gamma)) \equiv (\alpha \land \beta) \lor (\alpha \land \gamma)\) ( \(\land\) 对 \(\lor\) 的分配律 ) |
| \((\alpha \Rightarrow \beta) \equiv \neg \beta \Rightarrow \neg \alpha\) ( 逆否命题 ) | \((\alpha \lor (\beta \land \gamma)) \equiv (\alpha \lor \beta) \land (\alpha \lor \gamma)\) ( \(\lor\) 对 \(\land\) 的分配律 ) |
可以从一个复合命题推导出等价的命题,而不用列出真值表
推理规则 ¶
归结:\(\alpha \lor\beta, \neg \alpha\) 推出 \(\beta\)
| 推理规则 | 形式 | 说人话 |
|---|---|---|
| 假言推理 (Modus Ponens) | \(\frac{\alpha \rightarrow \beta, \alpha}{\beta}\) | 满足了前提条件,推出结论 |
| 与消解 (And-Elimination) | \(\frac{\alpha_1 \land \alpha_2 \land \cdots \land \alpha_n}{\alpha_i (1 \leq i \leq n)}\) | 众多条件抽一个 |
| 与导入 (And-Introduction) | \(\frac{\alpha_1, \alpha_2, \ldots, \alpha_n}{\alpha_1 \land \alpha_2 \land \cdots \land \alpha_n}\) | 果宝特工,归位 |
| 双重否定 (Double-Negation Elimination) | \(\frac{\neg \neg \alpha}{\alpha}\) | 否定之否定 |
| 单项消解或单项归结 (Unit Resolution) | \(\frac{\alpha \lor \beta, \neg \beta}{\alpha}\) | |
| 消解或归结 (Resolution) | \(\frac{\alpha \lor \beta, \neg \beta \lor \gamma}{\alpha \lor \gamma}\) 或 \(\frac{\alpha_1 \lor \alpha_2 \lor \cdots \lor \alpha_m, \neg \alpha_k}{\alpha_1 \lor \alpha_2 \lor \cdots \lor \alpha_{k-1} \lor \alpha_{k+1} \lor \cdots \lor \alpha_m} (\neg \alpha_k = \neg \beta)\) | 有一对相反的,可以抵消 |
归结法:反证法
例子
例 1:

例 2:
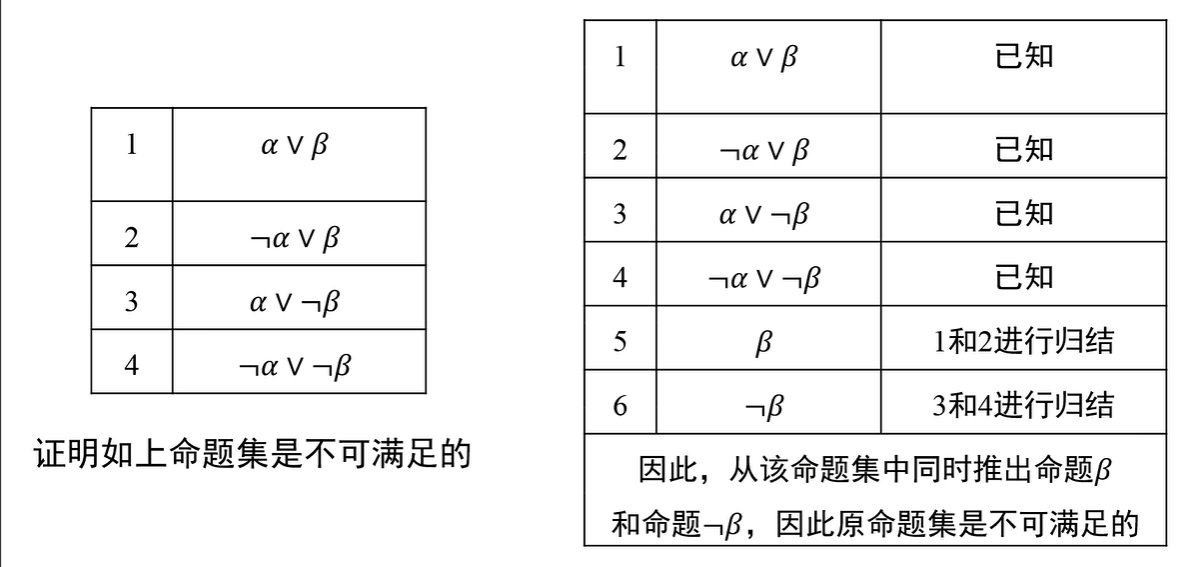
例 3:

命题范式 ¶
- 有限个简单合取式构成的析取式称为析取范式
- 由有限个简单析取式构成的合取式称为合取范式
- 析取范式与合取范式统称为范式 (normal form)
- 一个析取范式是不成立的,当且仅当它的每个简单合取式都不成立。
- 一个合取范式是成立的,当且仅当它的每个简单析取式都是成立的。
任一命题公式都存在着与之等值的析取范式与合取范式 (注意:命题公式的析取范式与合取范式都不是唯一的)
求 \(\neg (\alpha \rightarrow \beta) \lor \neg \gamma\) 的析取范式与合取范式
谓词逻辑——表达关系 ¶
命题逻辑有局限性,无法表示从属关系、个体关系等

不同原子命题蕴含个体、群体、关系等,命题逻辑无法表现;需要分析原子命题,分离其主语和谓语
个体、谓词、量词
谓词 ¶
- 谓词中个体变元用个体常量带入后就变成了命题,如 \(\text{car}(x)\) (\(x\) 是车)这个谓词中 \(x\) 用吉普车代替,则 \(\text{car}(\) 吉普车 \()\) 是命题。
大写字母表示谓词,有一元谓词和 n 元谓词(可以有若干个个体变量)
函数与谓词的区别
函数中个体变元用个体常量带入后,得到的仍然是个体(值域)
谓词中个体变元用个体常量带入后就变成了命题
如 \(\text{car}(x)\) (\(x\) 是车)这个谓词中 \(x\) 用吉普车代替,则 \(\text{car}(\) 吉普车 \()\) 是命题。
函数是从定义域到值域的映射;
谓词是从定义域到 \(\{ \text{True}, \text{False} \}\) 的映射
量词 ¶
全称量词 (universal quantifier, \(\forall\))
- 全称量词用符号 ∀ 表示,表示一切的、凡是的、所有的、每一个等。
- \(\forall x\) 表示定义域中的所有个体,\(\forall x P(x)\) 表示定义域中的所有个体具有性质 P
存在量词 (existential quantifier, \(\exists\))
- 存在量词用符号 ∃ 表示,表示存在、有一个、某些等。
- \(\exists x\) 表示定义域中存在一个或若干个个体,\(\exists x P(x)\) 表示定义域中存在一个个体或若干个个体具有性质 P
合式公式 ( 复杂谓词 )
- 命题常项、命题变项、原子谓词(不存在任何量词与联结词)是合式公式。
- 如果 \(A\) 和 \(B\) 是合式公式,那么 \(\neg A\)、\(A \land B\)、\(A \lor B\)、\(A \rightarrow B\)、\(A \leftrightarrow B\) 都是合式公式
- 如果 \(A\) 是合式公式,\(x\) 是个体变元,则 \(\exists x A(x)\) 和 \(\forall x A(x)\) 也是合式公式
- 有限次地使用上述规则获得的公式是合式公式
推理规则 ¶
- 全称量词消去 (Universal Instantiation, UI): \((\forall x) A(x) \rightarrow A(y)\)
- 全称量词引入 (Universal Generalization, UG): \(A(y) \rightarrow (\forall x) A(x)\)
- 存在量词消去 (Existential Instantiation, EI): \((\exists x) A(x) \rightarrow A(c)\)
- 存在量词引入 (Existential Generalization, EG): \(A(c) \rightarrow (\exists x) A(x)\)
真值 ¶
永真性:如果谓词公式 P 对个体域 D 上的任何一个解释都取得真值 T,则称 P 在 D 上是永真的 ; 如果 P 在每个非空个体域上均永真,则称 P 永真;如果谓词公式 P 对个体域 D 上的任何一个解释都取得真值 F,则称 P 在 D 上是永假的 ; 如果 P 在每个非空个体域上均永假,则称 P 永假。(T 和 F 是谓词逻辑真值表的 True 和 False)
可满足性 / 不可满足性:对于谓词公式 P,如果至少存在一个解释使得 P 在此解释下的真值为 T,则称 P 是可满足的;否则,则称 P 是不可满足的。
等价性:给定任何两个谓词公式 A 和 B,设它们有共同的个体域 E,若对 A 和 B 的任一组变元进行赋值,所得命题的真值相同,则称谓词公式 A 和 B 在 E 上是等价的,记作:A⇔B
命题符号化 ¶
(1)猫比老鼠跑得快。 (2)有的猫比所有老鼠跑得快。 (3)并不是所有的猫比老鼠跑得快。 (4)不存在跑得同样快的两只猫。
设 \(F(x,y)\) 表示 "x 比 y 跑得快 ",\(C(x)\) 表示 "x 是猫 ",\(M(x)\) 表示 "x 是老鼠 "。
(1) \((\forall x)(\forall y)((C(x) \land M(y)) \rightarrow F(x,y))\)
(2) \((\exists x)(C(x) \land (\forall y)(M(y) \rightarrow F(x,y)))\)
(3) \(\neg(\forall x)(\forall y)((C(x) \land M(y)) \rightarrow F(x,y))\)
(4) \(\neg(\exists x)(\exists y)(C(x) \land C(y) \land x \neq y \land \neg F(x,y) \land \neg F(y,x))\)
基础题
有如下事实:
- 所有伟大的厨师都是意大利人
- 所有意大利人都喜欢享用美食
- 迈克尔(Michael)或路易斯(Louis)是一位伟大的厨师
- 迈克尔不是一位伟大的厨师
因此,路易斯喜欢享用美食**
1. 定义合适的谓词(1.5 分
定义如下谓词:
\(GC(x)\): x 是一位伟大的厨师
\(I(x)\): x 是意大利人
\(EF(x)\): x 享用美食
2. 使用定义的谓词表述上述语句(2.0 分)
谓词逻辑表达:
1) \((\forall x)(GC(x) \Rightarrow I(x))\)
2) \((\forall x)(I(x) \Rightarrow EF(x))\)
3) \(GC(\text{Michael}) \lor GC(\text{Louis})\)
4) \(\neg GC(\text{Michael})\)
因此: 5) \(EF(\text{Louis})\)
3. 将谓词语句转换为标准子句(2.5 分)
转换为子句(量词实例化和蕴含消除):
1) \(\neg GC(x) \lor I(x)\)
2) \(\neg I(y) \lor EF(y)\)
3) \(GC(\text{Michael}) \lor GC(\text{Louis})\)
4) \(\neg GC(\text{Michael})\)
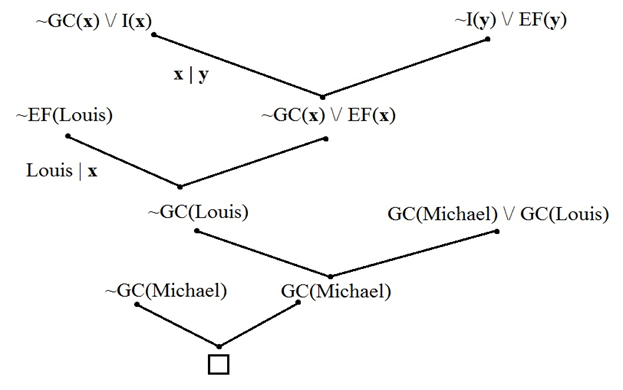
4. 应用归结方法证明结论 5,画出归结过程并标注出合适的合一(4 分)
否定结论:
1) ~EF(Louis)
证明案例


每一个奇数均存在一个大于它的奇数: - \(\text{odd}(x): x\) 是奇数 - \(\text{Great}(x, y): x 大于 y\) - \((\forall x)(\text{odd}(x) \rightarrow (\exists y)(\text{odd}(y) \land \text{Great}(y, x)))\)
证明:
- \((\neg \forall x) \text{Plane}(x) \rightarrow \text{on\_fly}(x)\)
- \((\exists x)(\neg \text{Plane}(x) \rightarrow \text{on\_fly}(x))\)
- \((\exists x)(\neg \text{Plane}(x) \lor \text{on\_fly}(x))\)
- \((\exists x)(\text{Plane}(x) \land \neg \text{on\_fly}(x))\)
- \(\text{Plane}(a) \land \neg \text{on\_fly}(a)\)
- \(\text{Plane}(a)\)
- \(\neg \text{on\_fly}(a)\)
- \((\forall x)(\text{plane}(x) \rightarrow (\text{in\_ground}(x) \lor \text{on\_fly}(x)))\)
- \(\text{plane}(a) \rightarrow (\text{in\_ground}(a) \lor \text{on\_fly}(a))\)
- \(\text{in\_ground}(a) \lor \text{on\_fly}(a)\)
- \(\text{in\_ground}(a)\)
- \(\text{Plane}(a) \land \text{in\_ground}(a)\)
- \((\exists x)(\text{plane}(x) \land \text{in\_ground}(x))\)
应用领域:专家系统 ¶
把某个领域的自然语言、文本语句进行逻辑化,使用谓词进行表达,把问题推给推理机,推理机就能得出结论