规则学习 ¶
约 1067 个字 预计阅读时间 4 分钟
概念学习:属于模型驱动学习中的一种,从给定的某一类别的若干正例和反例中获得该类别的一般定义。概念学习也可以看作是一个搜索问题的过程,它在预定义的假设空间中搜索假设,使其与训练样例有最佳的拟合度
定义:
给定一个样例集合以及每个样例是否属于某个概念的标注,怎样推断出该概念的一般定义,又称从样例中逼近
概念学习是指从有关某个布尔函数的输入输出训练样例中推断出该布尔函数
机器学习(埋坑)—— 概念学习(Concept Learning)-CSDN 博客
- 实例空间
- 假设空间
- 训练样例:训练样例的表示可由一个序偶对 \(<x,c(x)>\) 完成。其中 x 是一个训练样本,
- 正例
- 反例
- 目标概念:一个布尔函数
Find-S 算法 ¶
从 H 中最特殊假设开始,然后在假设覆盖正例失败时将其一般化
1) 将 \(h\) 初始化为 \(H\) 中最特殊假设 ( 即所有属性均为 \(\emptyset\) )
2) 对训练样例集 \(D\) 中的每个正样例 \(d^+\):
- 对 \(h\) 的每个属性约束 \(a_i\)
- 如果 \(x\) 满足 \(a_i\),那么不做任何处理
- 否则将 \(h\) 中 \(a_i\) 替换为 \(x\) 满足的另一个更一般约束
3) 输出假设 \(h\)
例子 ¶
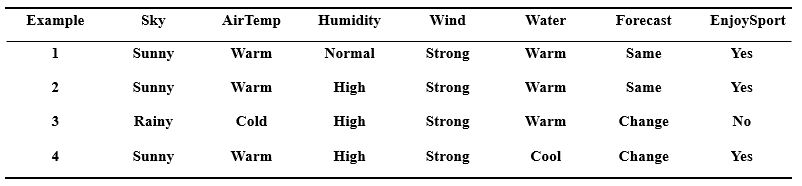
初始化最特殊假设:\(h \leftarrow < \emptyset, \emptyset, \emptyset, \emptyset, \emptyset, \emptyset>\)
输入正样例 1,一般化假设:\(h \leftarrow <Sunny, Warm, Normal, Strong, Warm, Same>\)
输入正样例 2,一般化假设:\(h \leftarrow <Sunny, Warm, ?, Strong, Warm, Same>\)
输入反样例 3,假设 h 保持不变(h 已经能够正确地识别反例)
输入正样例 4,一般化假设:\(h \leftarrow <Sunny, Warm, ?, Strong, ?, ?>\)
问题 ¶
-
收敛性问题:Find-S 算法无法确定是否拟合到目标概念
-
假设选择问题:Find-S 算法找到的是满足训练样例集 D 的最特殊假设 h,而没有考虑满足条件的最一般假设和介于二者之间的其他假设
-
健壮性问题:算法健壮性较差,当训练样例集 D 中出现错误样例时,会严重破坏算法
归纳偏置 ¶
1)假定目标概念必须在假设空间中 2)对于任何实例来说,若不符合最特殊假设,除非其为正例可由其他知识逻辑推出,否则均判别为反例
变型空间与候选消除算法 ¶
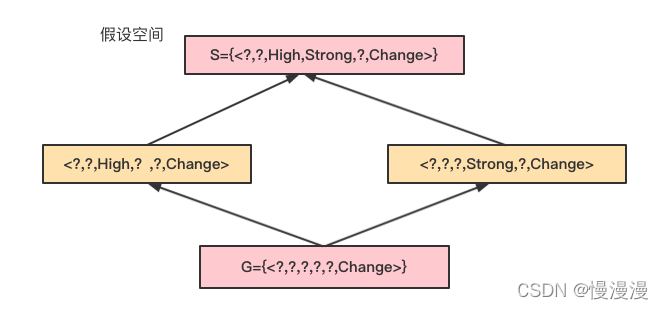
变型空间:与训练样例一致的所有假设的集合,即变型空间中任意一个假设都能覆盖所有的正例并排斥所有的反例。变型空间一般用极大一般假设 G 和极大特殊假设 S 来表示,所有位于 G 和 S 之间的假设都在变型空间内
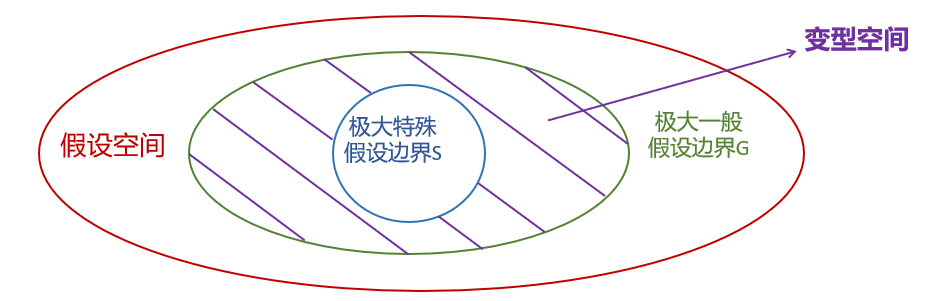
步骤 ¶
1) 初始化 \(G\) ( 所有属性均为 \(?\) );初始化 \(S\) ( 所有属性均为 \(\emptyset\) )
2) 对训练样例集 \(D\) 中的每个正样例 \(d^+\):一般化 \(S\)
对训练样例集 \(D\) 中的每个负样例 \(d^-\):特殊化 \(G\)
( 在更新 \(S\) 和 \(G\) 时,每一步均需要保证 \(G\) 包含 \(S\))
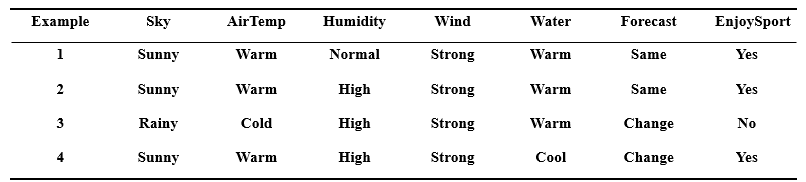
例子 ¶
| Example | Outlook | AirTump | Humidity | Wind | Water | Forecast | EnjoySport |
|---|---|---|---|---|---|---|---|
| D1 | Sunny | Warm | Normal | Strong | Warm | Same | No |
| D2 | Sunny | Warm | High | Strong | Warm | Same | No |
| D3 | Rainy | Cold | High | Strong | Warm | Change | Yes |
| D4 | Sunny | Warm | High | Strong | Cool | Change | Yes |
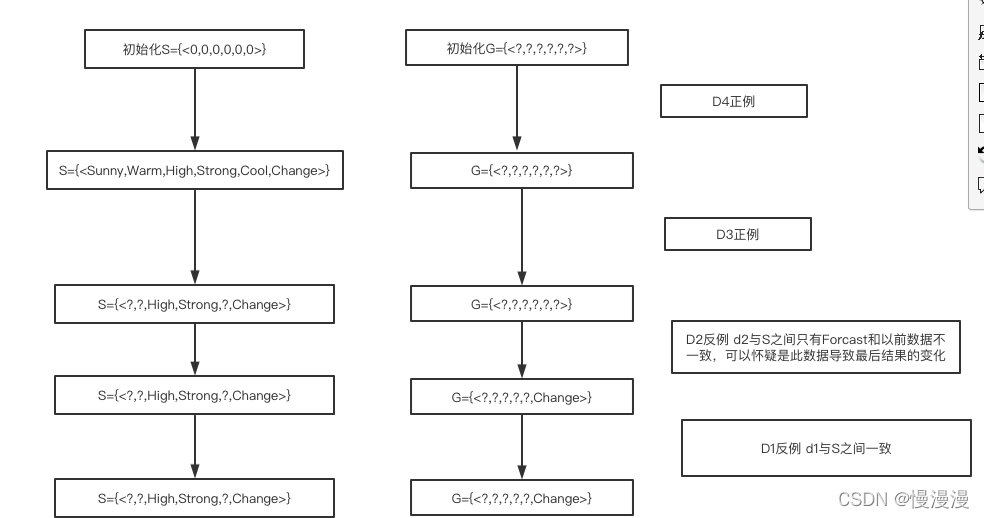
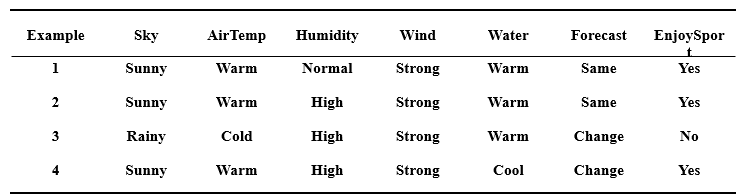
例 2
在候选消除算法中,如果训练样例按 EnjoySport 例子中的逆序出现,请分步给出 S 和 G 边界集合。

归纳偏置 ¶
1)假定目标概念必须在假设空间中 2)对于任何实例来说,若不在变型空间中,除非其为正例可由其他知识逻辑推出,否则均判别为’new instance’或’don’t know’
应用 ¶
-
变型空间和候选消除算法应用于质谱分析中的规则推理
-
变型空间和候选消除算法应用于学习搜索控制规则
-
具有类比学习和概念学习能力的混合学习机制算法 LM 在专家系统中引入机器学习机制,解决构造专家系统的瓶颈问题 ' 知识获取 ',使专家系统体现出更高的智能