Interpretable ML¶

Explainable ML refers to methods and techniques in the application of ML systems such that the results of the solution can be understood by human experts and users

transparent models & opaque models

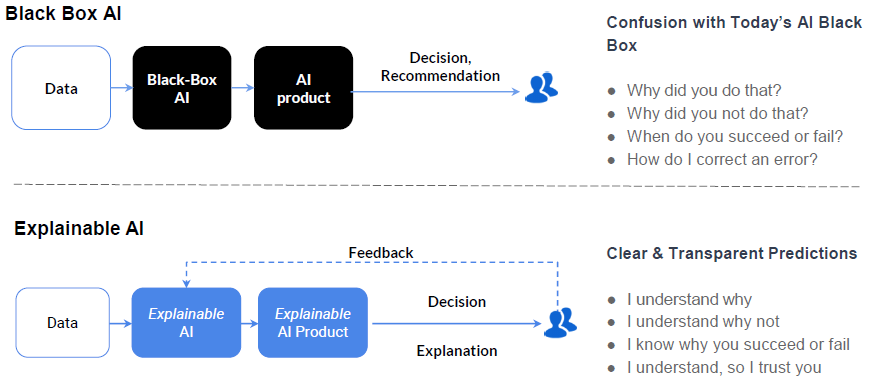
Feature relevance (or feature attribution) is also applied with non-image data for quantifying the influence of each input variable toward the model decision

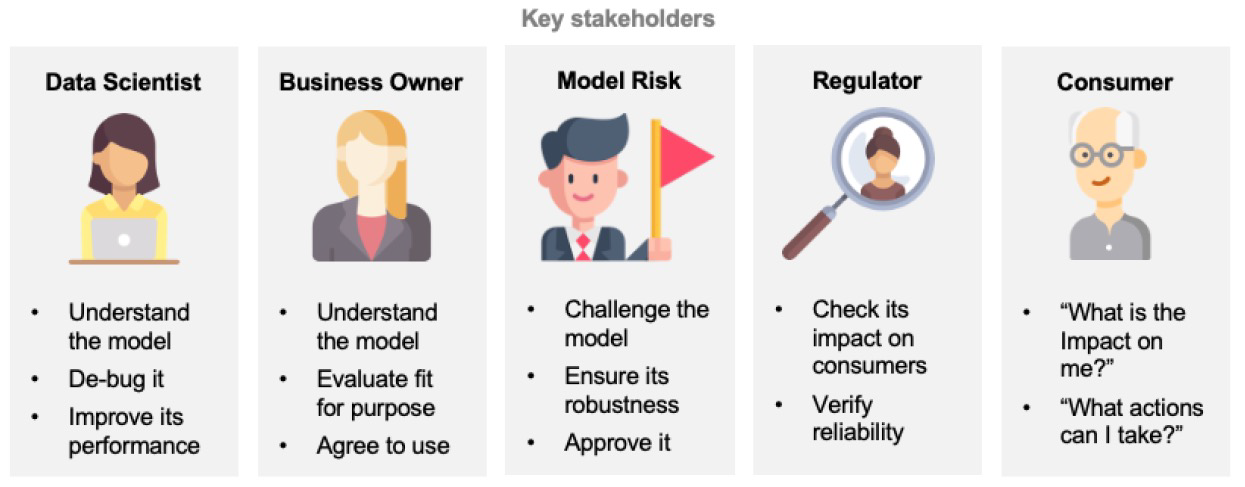
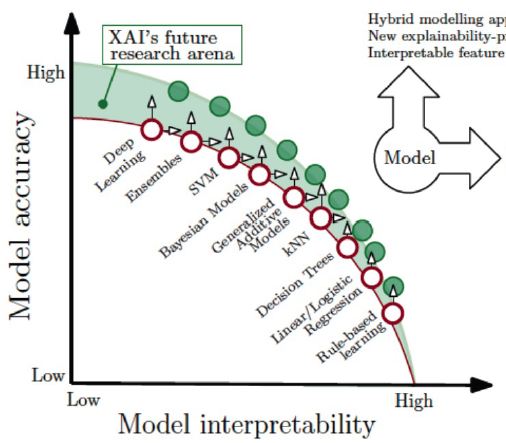
Currently, the best performing models in terms of accuracy are the least interpretable

Pixel level¶

!!! note "which input pixels are important when a model classifies one input example? (Local Explanation)"

Vanilla BackProp¶

The approach uses backpropagation to visualize the gradients with respect to each pixel of an image

[1312.6034] Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps

Guided BackProp¶

Occlusion Maps¶

Systematically occlude different portions of the input image with a grey square, and monitor the output of the classifier

E.g., in the image, the strongest feature is the dog’s head - Occlusion maps is an older and computationally expensive method

CAM¶

CAM produces a heatmap for the pixels that activate the most model’s prediction of a specific class of objects

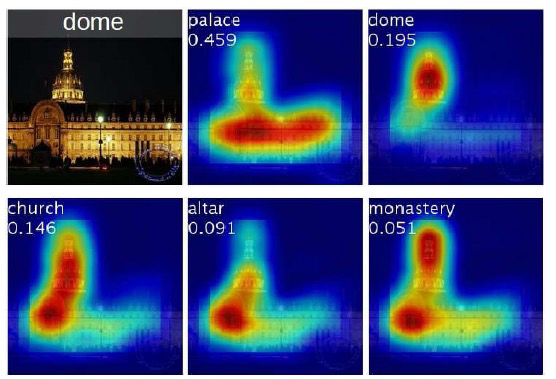
Grad-CAM¶

Grad-CAM is an extension of the CAM approach

• It employs gradient backpropagation to improve the heatmaps
• Compare Grad-CAM to Guided BackProp for the classes ‘Cat’ and “Dog’ in the image

Guided Grad-CAM¶

Integrated Gradients¶

Integrated gradients employs the integral of the gradients of a black-box model \(F\) along a straight-line path from a baseline input \(z\) to an input instance \(x\)

LRP¶

Layer-wise Relevancy Propagation

LRP calculates the attribution (i.e., relevance, importance) of each pixel \(i\) in the input image x to the model prediction \(f(\mathscr{x})\)

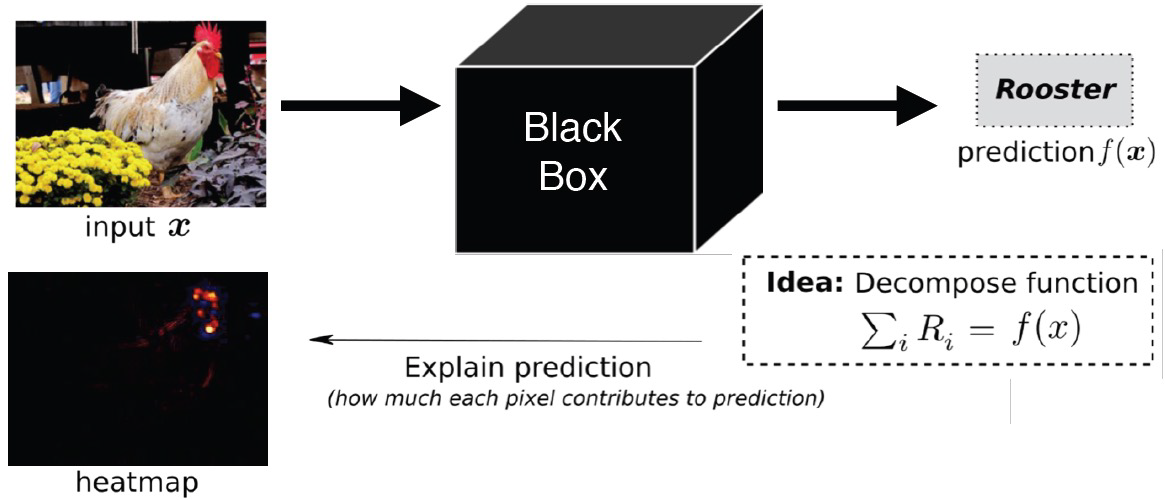
feature level¶

LIME¶

LIME 算法：模型的可解释性（代码实现）-CSDN 博客

全称 Local Interpretable Model-agnostic Explanations，可以理解为模型的解释器。

"Why Should I Trust You?": Explaining the Predictions of Any Classifier

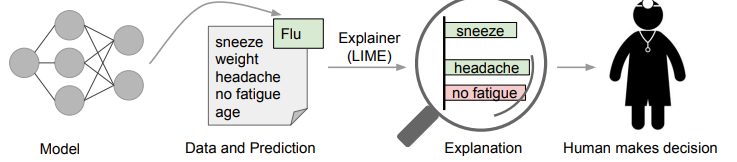- 用户需要信任预测结果：举一个论文中提到的例子，一个医学模型判断病人患病，通过 LIME 算法同时给出病人的病史症状包括喷嚏、头痛等特征，医生利用自己的先验知识，就能更好地借助模型做出决定。

• 建模者需要信任模型：每个算法都需要对模型整体信任度有一定的衡量，意思就是模型是否学到了我们所预期的东西。论文中举出一个文章分类的例子，判断该文章与“基督教“有关还是与”无神论教“有关，分类器本身达到了 90% 的准确率。但是利用 LIME 解释器，发现”无神论教“的重要特征，是”Posting“( 邮件标头的一部分 )，这个词与无神论本身并没有太多的联系。这意味着尽管模型准确率很高，但所学习到的特征是错误的。

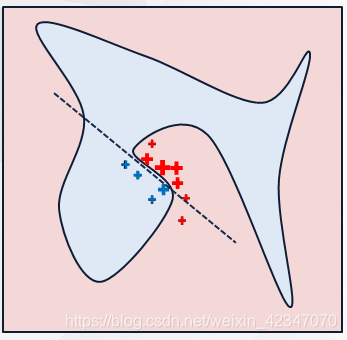
如图所示，红色和蓝色区域表示一个复杂的分类模型（黑盒），图中加粗的红色十字表示需要解释的样本，显然，我们很难从全局用一个可解释的模型（例如线性模型）去逼近拟合它。但是，当我们把关注点从全局放到局部时，可以看到在某些局部是可以用线性模型去拟合的。具体来说，我们从加粗的红色十字样本周围采样，所谓采样就是对原始样本的特征做一些扰动，将采样出的样本用分类模型分类并得到结果（红十字和蓝色点），同时根据采样样本与加粗红十字的距离赋予权重（权重以标志的大小表示）。虚线表示通过这些采样样本学到的局部可解释模型，在这个例子中就是一个简单的线性分类器。在此基础上，我们就可以依据这个局部的可解释模型对这个分类结果进行解释了。

SHAP¶

shapley Values

一群拥有不同技能的参与者为了集体奖励而相互合作。那么，如何在小组中公平分配奖励？

机器学习中的 Shapley 值怎么理解？

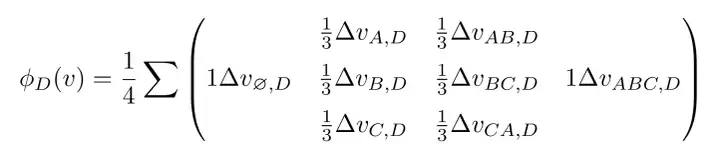
考察一个对象对剩余对象的子集，有什么边际影响。

这才是 Shapley 值背后真正的力量和吸引力。然而，这是有代价的。对于一组参与游戏的 \(n\) 个玩家，你将需要分析 \(2^n\) 个子集才能计算 Shapley 值。

有一些方法可以使计算更加实际可行，在引言中我提到了 SHAP 框架，它的主要优点是，当将 Shapley 值应用于机器学习时，它能够更有效地计算 Shapley 值。

Concept level¶

!!! note "which high-level concepts are important when a model classifies one class of inputs across the entire dataset? (Global Explanation)"

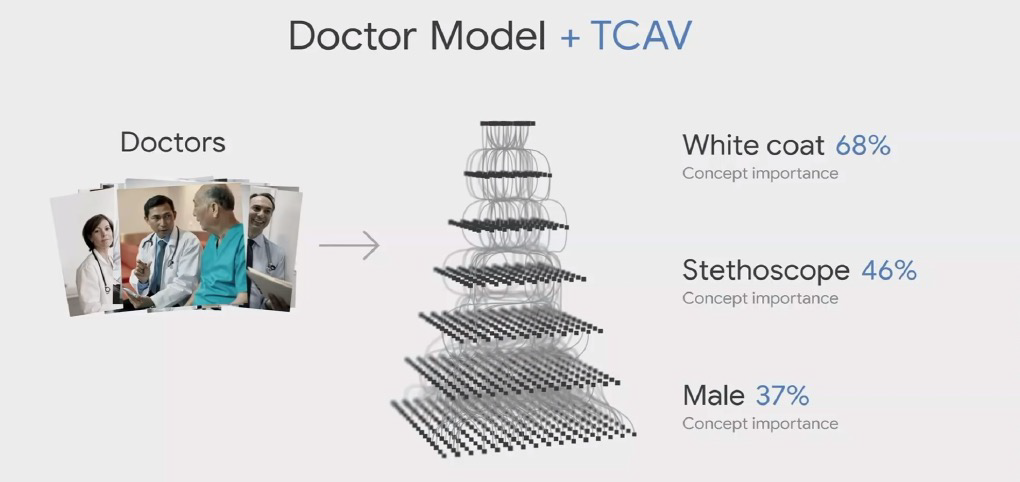
TCAV¶

1. Represent the concept as a vector (referred to as Concept Activation Vector (CAV) 决策边界线的正交向量 )
2. Quantify the sensitivity of an image to the CAV vector
3. Measure the importance of the concept to multiple images of the same class

ACE¶

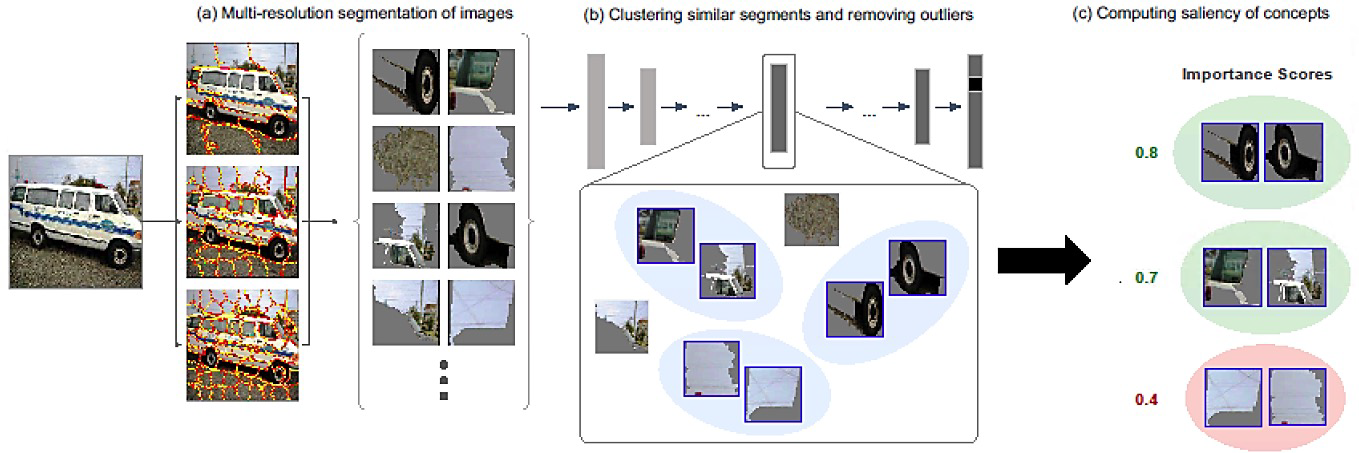
ACE advantage over the TCAV approach: It does not require a manual selection of a set of positive and negative images for a concept

Instance level¶

prototype & criticism¶

Prototypes: representative examples of the class

Criticisms: examples of the class that are not well represented by the prototypes

Maximum Mean Discrepancy (MMD) to measure the discrepancy between two distributions, given by

Prototypes¶

To find prototypes: 1. Start with an empty set of prototypes. 2. While the number of prototypes is below the chosen number $ m $: - For each instance in the dataset, check how much MMD is reduced when the instance is added to the set of prototypes. - Add the data instance that minimizes MMD to the set of prototypes. 3. Return the set of prototypes.

Criticisms¶

To find criticisms, the following witness function is used: $$ text{witness}(x) = frac{1}{n} sum_{i} k(x, x_i) - frac{1}{m} sum_{j} k(x, z_j) $$ - The witness function evaluates which of two distributions fits the instance $ x $ better.

counterfactuals explanation¶

change the input feature vectors

因果推断可解释性 之 反事实解释综述（三） - 知乎