07 | 降维 ¶

• dimensionality reduction tries to transform high-demensional data into a low-dimensioanl space while preserving the data structure.
• data might lie on low-dimensional manifolds.

Curse of Dimensionality

– For fixed \(n\), as \(p\) increases, the data become sparse – As \(p\) increases, the number of possible models explodes(computation burden, variable selection necessary)

kNN | k 近邻 ¶

KNN 是一种经典的监督学习方法，也是 lazy learning 的代表，不需要任何训练

1. 选择距离度量
2. 选择最近的 k 个样本 - 如果是回归任务，那么结果就是k个样本的平均or加权平均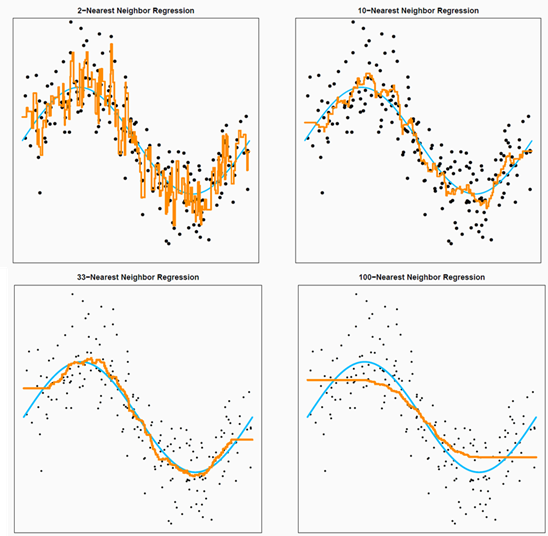； - 如果是分类任务，则采用投票 or 加权投票(majority vote)

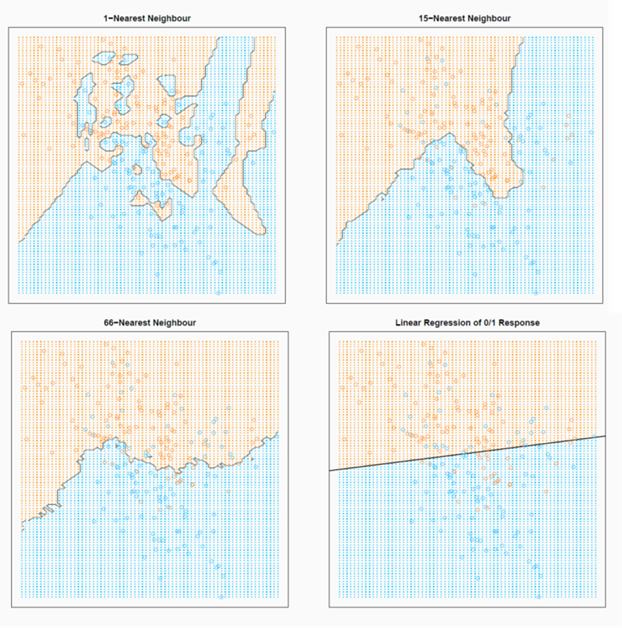
1NN¶

1NN 是 kNN 的特殊情况，k=1，这个时候模型复杂度很高

错误率分析 ¶

给定测试样本 \(x\)，若其最近邻样本为 \(z\)，则最近邻分类器出错的概率就是 \(x\) 与 \(z\) 类别标记不同的概率，即

假设样本独立同分布，且对任意 \( x \) 和任意小正数 \( \delta \)，在 \( x \) 附近 \( \delta \) 距离范围内总能找到一个训练样本；换言之，对任意测试样本，总能在任意近的范围内找到式中的训练样本 \( z \)。令 \( c^* = \arg\max_{c \in \mathcal{Y}} P(c \mid x) \) 表示贝叶斯最优分类器的结果，有

• 假设是 \(\delta\) 范围内必定能找到一个点（1NN 的假设接近）
• 表明如果噪声比较小的话，选择 1NN 是合理的

bias-var 分析 ¶

1NN 的时候，当点数很大的时候，1NN 可以无限接近于真实点，模型的 bias 约等于 0；模型的 var（不同数据集合下的表现）约等于 \(\sigma^2\)

不同数据集间的差距就是系统的噪声，可以理解为 var 体现了这一点

knn 的时候，variance 约为 \(\frac{\sigma^2}{k}\),\({bias}^2\) 会增加，因为 neighbours 远离 \(x_0\)

• 当 k 增大的时候，模型复杂度降低，模型趋于整体的均值，bias 增加，var 降低。
• k 较小的时候，模型复杂度高，模型的 bias 低，但是 var 比较高

过拟合和模型复杂度 ¶

Degrees-of-freedom and model complexity are related concepts, and they can be used to prevent over-fitting

对于 kNN 来说，其自由度是 \(\frac{n}{k}\) - 1NN 的自由度是n - nNN 的自由度是1

k 趋于无穷大，\(\frac{n}{k}\) 趋于 0 时，KNN 是相合的

计算 ¶

• Lazy Learning: Need to store the entire training data for future prediction
• Prediction can be slow. Needs to calculate the distance from x0 to all training sample and sort them.
• Some fast nearest neighbor search algorithms such as k-d tree
• A distance measure may affect accuracy

但是如果求解的问题有低维的结构（manifold 流形），那么精度会高一点

MDS | Multiple dimensional Scaling¶

第一步——求解距离矩阵 D

def get_distance_matrix(data):
	expand_ = data[:, np.newaxis, :]
	repeat1 = np.repeat(expand_, data.shape[0], axis=1)
	repeat2 = np.swapaxes(repeat1, 0, 1)
	D = np.linalg.norm(repeat1 - repeat2, ord=2, axis=-1, keepdims=True).squeeze(-1)
	return D

第二步——求解内积矩阵 B

def get_matrix_B(D):
	assert D.shape[0] == D.shape[1]
	DD = np.square(D)
	sum_ = np.sum(DD, axis=1) / D.shape[0]
	Di = np.repeat(sum_[:, np.newaxis], D.shape[0], axis=1)
	Dj = np.repeat(sum_[np.newaxis, :], D.shape[0], axis=0)
	Dij = np.sum(DD) / ((D.shape[0])**2) * np.ones([D.shape[0], D.shape[0]])
	B = (Di + Dj - DD- Dij) / 2
	return B

第三步——求解 Z 矩阵

\(B = Z^T Z\)

def MDS(data, n=2):
	D = get_distance_matrix(data)
	B = get_matrix_B(D)
	B_value, B_vector = np.linalg.eigh(B)
	Be_sort = np.argsort(-B_value)
	B_value = B_value[Be_sort]               # 降序排列的特征值
	B_vector = B_vector[:,Be_sort]           # 降序排列的特征值对应的特征向量
	Bez = np.diag(B_value[0:n])
	Bvz = B_vector[:, 0:n]
	Z = np.dot(np.sqrt(Bez), Bvz.T).T
	return Z

PCA¶

降维技巧 | 导论与流形学习：⅕

第一阶段找了一个新的坐标系来表示数据，这个新的坐标系不是随便找的，是要求能最大限度的看出每个轴上的数据变化大小

第二阶段在新坐标系下取前 k 个变化最大的轴上的数据（最大特征值对应的轴），从而实现降维。

一文让你彻底搞懂主成成分分析 PCA 的原理及代码实现 ( 超详细推导 )_pca 主成分分析图解释 -CSDN 博客

如何直观地理解「协方差矩阵」？

【数据降维 - 第 4 篇】多维尺度变换（MDS）快速理解，及 MATLAB 实现 - 知乎

利用 PCA 降维的手工计算实例 _ 给定如下数据 , 采用 pca 计算降维时所用的特征向量 -CSDN 博客

kernel PCA¶

PCA 和 SVD 的关系：

SVD：

U 是特征向量，S 是特征值，V 是特征向量

协方差矩阵告诉我们变量的方差和联合方向

流形学习 ¶

LLE¶

原始空间到子空间

度量学习 ¶

距离 ¶

欧式距离：在每个方向上同等重要；有缘千里来相会；无缘对面手难牵

马氏距离：

NCA | Neighborhood Components Analysis¶