05 | Bayes 贝叶斯分类器 ¶

约 2851 个字预计阅读时间 11 分钟

本章知识点

计算给定一个table，算好瓜坏瓜

公式推导 E step公式 M step公式

$x$ sample

$y$ state of the nature

$P(y|x)$ given $x$,what is the probability of the state of the nature

条件概率： $$ P(A|B) = frac{P(A,B)}{P(B)} $$

先验概率 | prior: $P(A)$the probability A being True. this is the knowledge

反映了我们关注的标签在自然界中 ( 无人为干预的情况下 ) 的数量分布情况（在某个特征下也可以）。例如：我们可以看在 lightness 特征条件下 See bass 和 salmon 这两个标签的数量情况。更简单的来讲，先验就是在我们不知情的情况下猜测的标签种类。（我们倾向于猜测炸弹不会爆炸，因为其先验概率很小）

如果没有先验概率的情况下，我们可能会认为 salmon 和 sea bass 的捕捉概率是相等的。这种假设并不适用于任何情况。$P(y_{1} )=P(y_{2} )$

如果是二分类问题 $P(y_{1} )+P(y_{2} )=1$
如果只根据先验信息进行决策 - 即如果y1的概率大于y2则认为是y1，否则就是y2. - 先验概率不一定准确，没有用到事物本身的feature，纯在猜测。

似然性 | likelihood: $P(B|A)$the probability of B being true,given A is true

概率和似然

概率： 在一件事的结果未知的情况下，通过事件自身的性质估计事件各个结果的可能性的大小，就是事件各个结果发生的概率。（抛硬币：硬币有两面，所以两面分别朝上的概率都是百分之五十，概率只有在事件发生前是有意义的，因为当硬币抛出后，结果就已经确定了。）
似然： 基于事件已经确定的结果来推测产生这个结果的可能环境（环境中的某些参数）。（抛硬币：直接抛硬币 10000 次，其中 8000 次正面朝上，2000 次反面朝上，我们会认为硬币的构造比较特殊，进而推测该硬币的具体参数）

后验概率 | posterior: $P(A|B)$

贝叶斯定理 $$ P(A|B) = P(A)frac{P(B|A)}{P(B)} $$

\[ [后验概率] = [先验概率]\times[后验概率] \]

【官方双语】贝叶斯定理，使概率论直觉化 _ 哔哩哔哩 _bilibili

rationality is not about knowing facts, it's about recognizing which facts are relevant

新证据不能直接决定看法，而是应该更新你的观点

最大似然概率决策 MLE

\[ P(y_i|x) = \frac{P(x|y_i) P(y_i)}{P(x)} \]

Bayes Decision Rule

Decide $y_1$, if $P(y_1|x)> P(y_2|x)$,otherwise $y_2$

因为 $P(x)$ 与类别 $y_i$ 无关，所以可以省略

最小化错误概率

最小错误其实和最大后验概率是等价的，因为最小错误就是最大化后验概率。（使用二分类来理解）

例子

Bayesian Risk | 贝叶斯风险 ¶

并不是所有的错误代价都是相同的

如果将两个类别互相识别错误的风险相当的前提下，类别只需要比较两者的后验概率即可，就与之前绘制直方图类似。如果两者不相等，则需要依据风险函数比较大小进行类别判定。

\[ \begin{align*} E_{ij} = E(\hat{y_i}|y_j)\\ R(\hat{y_1}|x) = E_{11} P(y_1|x)+E_{12}P(y_2|x) = E_{12}P(y_2|x)\\ R(\hat{y_2}|x) = E_{21} P(y_1|x)+E_{22}P(y_2|x) = E_{21}P(y_1|x)\\ \end{align*} \]

决策方法：选风险最小的，decide $y_1$ if $R(\hat{y_1}|x) < R(\hat{y_2}|x)$

二分类中：当 likelihood ratio 超过某个与 x 无关的阈值时候，就做决策

\[ \begin{align*} E_{21}P(x|y_1)P(y_1) > E_{12}P(x|y_2)P(y_2)\\ \frac{P(x|y_1)}{P(x|y_2)} > \frac{E_{12}P(y_2)}{E_{21}P(y_1)}\\ \end{align*} \]

如果 $E_{12} = E_{21}$，最小化风险函数 Risk 就是最大化后验概率 P(yi|x)

你会觉得要让等式左边的 R 越小，等式右边的 P 不是也该越小吗？为什么要最大化呢？仔细看下表你就会发现 R 中的 $\hat{y}$ 的下标和 P 中的 $y$ 的下标是不一样的，你要 $\hat{y_1}$ 的 Risk 值越小，$\hat{y_2}$ 对应的 P 值就越小，$y_1$ 对应的 P 值就应该越大，所以确实是 given x 条件下 $y_1$ 的后验概率越大

多分类的情况：seek a decision rule that minimizes the probability of error or maximizes the accuracy;

\[ \begin{align*} E(\hat{y_i}|y_j) = \begin{cases} 0 & if\ i=j\\ 1 & if\ i\ne j \end{cases} \end{align*} \]

如何理解贝叶斯最优分类器

假设我们已经“上帝视角”地获得了 $ P(Y|x) $，即知道在每个 $ x $ 的条件下，每个类别 $ Y $ 的概率。基于这些概率，贝叶斯最优分类器会选择具有最大后验概率的类别作为最终的决策结果。

假设我们在做垃圾邮件分类，已经知道：
- $ P(Y = 1 | x) = 0.8 $（即这封邮件是垃圾邮件的概率为 0.8） - $ P(Y = 0 | x) = 0.2 $（即这封邮件是非垃圾邮件的概率为 0.2）

根据贝叶斯最优分类器的规则，会将该邮件判断为垃圾邮件（$ \hat{y} = 1 $），错误率是 0.2。

回顾 ¶

贝叶斯的框架 - 知道先验概率P(yi)，知道似然P(x|yi)，我们就可以得到一个最优的分类器。 - 现实生活中，很难获取到准确的似然的信息（特征维度太高或者特征并不充分）。 - 常用的做法：利用训练数据去估计出先验概率和似然，再去做贝叶斯决策。

classifier assigns a feature when:

\[ g_i(x) > g_j(x), \forall j \neq i \]

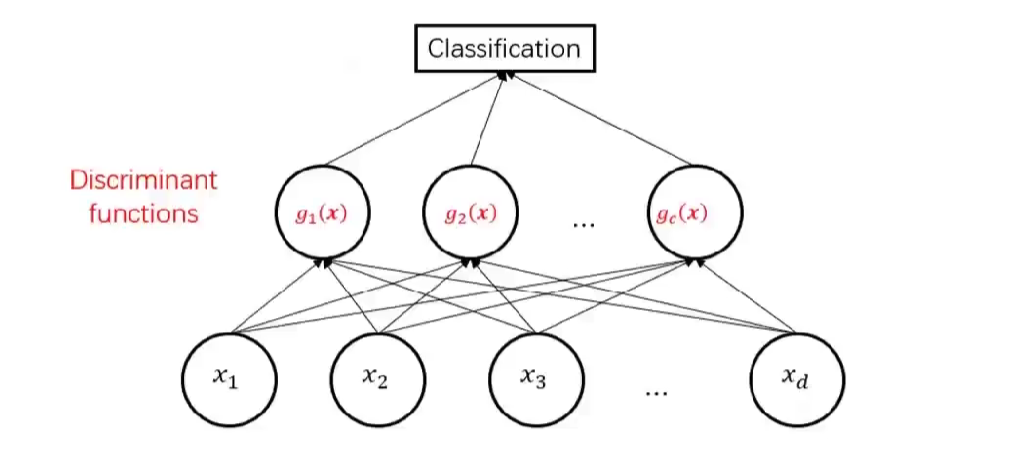中间的节点是一个分类器

判别函数是先验
判别函数是后验：贝叶斯决策
似然函数：极大似然估计
期望风险最小化：贝叶斯风险

极大似然法 maximum likehood ¶

概率和似然

这两个概念我经常有点糊涂

所谓概率就是已知参数 $\theta$ 的情况下，求 $X$ 的分布

而似然是指在给定 X 的情况下，去预估参数 $\theta$，

根据已有的数据 ( 相当于 $\textbf{X}$) 学到相应的分布 ( 即 $\theta$), 此概念对应 training 阶段 , 即在训练阶段 , 是根据已有的 $X$ 来估计其真实的数据分布服从什么样的分布 $\theta$

一个质量不均的骰子，投了很多次，求一个分布

Decision Regions and surfaces

learning 的过程其实就是将 feature space 分成不同的 decision regions
现实生活中，由于只能从有限的样本中学习，所以只能得到 likelihood 和先验的估计值

离散形式极大似然估计

先验概率：将频率估计为概率 $P\left(y_{k}\right)=\frac{N_{y_{k}}}{N}$

似然：在类别为 $y_k$ 的样本中特征为 $x_i$ 样本的占比。$P\left(x_{i} \mid y_{k}\right)=\frac{\left|x_{i k}\right|}{N_{y_{k}}}$

连续形式极大似然估计

discretize: the range into bins，对于体重来说，可以 50-100kg，100-150kg，150-200kg。再将数据段离散成不同的类别即可。
two-way split: 暴力分为两个段，设置一个中间值，小于中间值的设为一类，大于中间值的设为另一类。
Probability Density estimation: assume attribute follows a normal distribution or some other distribution

朴素贝叶斯 ¶

curse of dimensionality: feature space becomes sparse

假设特征之间是独立的

\[ \begin{align*} P(y|x_1,\dots,x_p) \propto P(x_1,\dots,x_p | y) P(y)= P(y)P(x_1|y)P(x_2|y)\dots P(x_p|y)\\ \end{align*} \]

好处： - robust to isolated noise points - can handle missing values - robust to irrelevant features - 可解释性非常好 - 计算量非常小 - 在实践中表现好的原因：数据中的特征之间的关系很弱；或者就算等式两侧不相等，其大小的相对关系仍然是一致的

问题： - 上述假设在实际中可能并不成立 - float point underflow - 0 probability - laplace smoothing: $P(x_i| y_k) = \frac{|x_{ik}|+1}{N_{y_k}+K}$,K是label的数量

改成取 $\ln$ 的原因

最重要的不是值本身，而是相对大小为了避免向上溢出，和向下溢出（浮点数问题），take a log

例题

处理数据 ¶

连续型需要估计参数，比如均值和方差

需要记住高斯分布的公式

\[ P(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]

离散型使用计数的方法

朴素贝叶斯处理连续值

假设我们有一个分类问题，要预测某个花的类型（类别 $C_1, C_2$），数据有一个特征是花瓣长度（连续值）。

训练数据：
$C_1$: 花瓣长度 = [1.2, 1.5, 1.3, 1.7]
$C_2$: 花瓣长度 = [3.2, 3.8, 3.6, 3.4]

估计参数： - 对 $C_1$：计算均值 $\mu_1$ 和标准差 $\sigma_1$ [ mu_1 = frac{1.2 + 1.5 + 1.3 + 1.7}{4} = 1.425,quad sigma_1 = sqrt{frac{(1.2-1.425)^2 + cdots}{4}} approx 0.18 ] - 对 $C_2$：计算均值 $\mu_2$ 和标准差 $\sigma_2$ [ mu_2 = 3.5,quad sigma_2 approx 0.24 ]
计算概率密度： - 假设测试样本的花瓣长度为 $x = 1.4$： [ P(x|C_1) = frac{1}{sqrt{2pi} cdot 0.18} expleft(-frac{(1.4-1.425)^2}{2 cdot 0.18^2}right) approx 2.21 ] [ P(x|C_2) = frac{1}{sqrt{2pi} cdot 0.24} expleft(-frac{(1.4-3.5)^2}{2 cdot 0.24^2}right) approx 0.001 ]
结合先验概率： - 若先验概率相等，则取概率密度较大的类别，即 $P(C_1|x) > P(C_2|x)$，预测类别为 $C_1$。

半朴素贝叶斯 ¶

常见方法 - SPODE：super parent one-dependence estimator - TAN：tree-augmented naive bayes - AODE：averaged one-dependence estimator

贝叶斯网络 ¶

构建 ¶

评分函数 ¶

最小描述长度：MDL|minimal description length

\[ s(B|D) = f(\theta)|B| - LL(B|D) \]

$|B|$ 是网络的大小，$LL(B|D)$ 是网络的似然度，$f(\theta)$ 是一个参数，用来平衡网络的大小和似然度

inference 推断 ¶

精确推断：直接根据贝叶斯网的定义的联合分布计算

近似推断 - 吉布斯采样 - 进行T次采样，逐个考察每个非证据变量 - 变分推断 - 相互独立，同种机制生成 - 盘式jis

EM 算法 ¶

极大似然估计：

\[ LL(\theta|x,z) - \nP(x,z|\mathcal{\theta}) \]

何谓 likelihood 似然 - 知乎

一个样本的似然计算：已知某个样本，对于某个参数，代入密度函数，这可能性就算出来了。

一堆样本的联合似然函数计算：假设样本采样是独立同分布的，也就是它们之间是独立的。然后，似然函数，就是每个样本的似然连乘。

为何 log 似然函数，把连乘变求和，方便后续最大似然估计，求导。

最大似然估计就是从一堆参数值中，找一个最有可能的参数。这就是为何用到对似然函数去求导 ( 高数的事情了 )，找最值。

简介与思想 ¶

EM 算法，全称 Expectation Maximization Algorithm，译作最大期望化算法或期望最大算法，它是一种迭代算法，用于含有隐变量（hidden variable）的概率参数模型的最大似然估计或极大后验概率估计。