02 | Linear Regression¶

y 是一个连续的值； 区别于classification，y是一个离散的值

Polynomial Curve Fitting¶

\(f(x,\omega) = \omega_0 + \omega_1x + \omega_2x^2 + \omega_3x^3 + \dots + \omega_Mx^M = \sum_{j=0}^{M}\omega_jx^j\)

loss function: MSE:

\(MSE(\omega) = \frac{1}{N}\sum_{i=1}^{N}(y_i - f(x_i,\omega))^2\)

模型是已知的，\(\omega\) 未知，通过最小化 MSE 来求解 \(\omega\)

• 最小二乘法

只能用于线性回归

using matrix notation for convenience: \(X = [1,x,x^2,x^3,...,x^n], y = [y_1,y_2,...,y_n]^T\)

\(Loss(\omega) = (y - X^T\omega)^T(y - X^T\omega)\)

梯度： \(\nabla_{\omega}Loss(\omega) = -2X(y - X^T\omega)\)

令梯度为 0，求解 \(\omega\)，得到 \(\omega = (X^TX)^{-1}X^Ty\)

• Gradient Descent | 梯度下降法 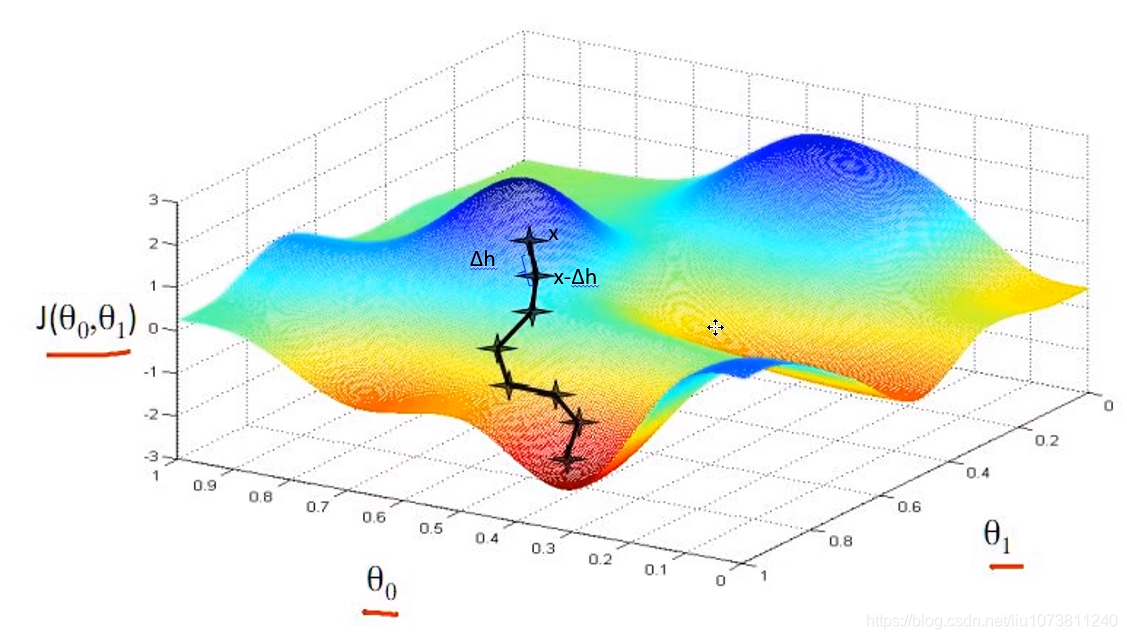步长的大小：学习率 Time complexity: \(O(ndt)\),t是迭代次数,d是特征的数量,n是样本的数量

stochastic gradient descent | 随机梯度下降法 - randomly select b(batch size) samples from the training set - Time complexity: \(O(bdt)\)

• Quasi Newton Method | 拟牛顿法

模型 ¶

损失函数 | 统计模型 ¶

如果将小批量的总损失替换为小批量损失的平均值，需要如何更改学习率？

如果将小批量的总损失替换为小批量损失的平均值，则需要将学习率乘以批量大小。这是因为在计算梯度时，我们使用了小批量中所有样本的信息。因此，如果我们将小批量的总损失替换为小批量损失的平均值，则相当于将每个样本的梯度除以批量大小。因此，我们需要将学习率乘以批量大小，以保持相同的更新步长

损失为什么求平均：更好调学习率，相当于学习率之和梯度有关，和 batch size 没有关系

每次算梯度的时候要记得清零，不然会做累加

l1 loss¶

不常用绝对差值而用平方损失：不好求导

有不平滑性，可能不稳定

离远点较远的时候，不一定希望有一个很大的梯度

l2 loss¶

Huber Robust loss¶

softmax 回归 ¶

• 不仅对硬分类感兴趣，还对软分类（概率）感兴趣

直接使用实数对应不太合适，所以使用向量来代表分类

为什么使用 ¶

• 线性有可能有负数，概率应该是非负的
• 概率之和需要为 1

交叉熵 ¶

信息论：

信息量 ： 不确定 -》确定的难度

可以理解为惊异程度，不确定度更大，则信息量更大

系统的熵

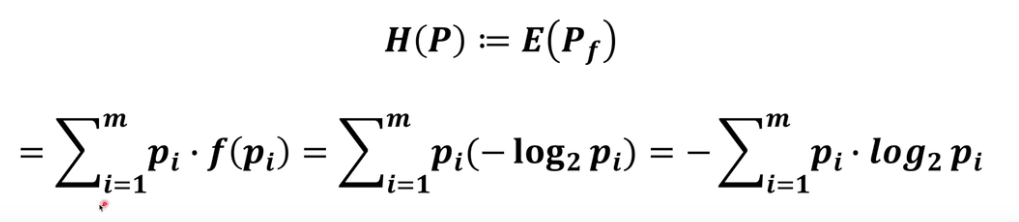
KL 散度

交叉熵

衡量两个概率的区别

我们可以把交叉熵想象为“主观概率为 \(Q\) 的观察者在看到根据概率 \(P\) 生成的数据时的预期惊异”。

（i）最大化观测数据的似然； （ii）最小化传达标签所需的惊异。

优化算法 | 优化模型 ¶

随机梯度下降：随机采样

关注的不是收敛快不快，而是收敛到哪一个点；牛顿法可能不平坦

训练过程 ¶

对于每一个小批量，我们会进行以下步骤 :

• 通过调用 net(X) 生成预测并计算损失 l（前向传播）。
• 通过进行反向传播来计算梯度。
• 通过调用优化器来更新模型参数。

训练框架 ¶

epoch: 训练轮次 iter 训练小批量

nn 模块定义了大量的神经网络层和常见损失函数。

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad() # 清除梯度，防止累计
        l.backward() # 自动计算梯度
        trainer.step() # 优化算法
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

初始化 ¶

可以使用固定的初始值，但是不能为 0

读取 ¶

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

batchsize 中最后一个 batch 中多余的样本： 1. 丢掉 2. 再随机采样，补满 3. 直接使用小样本

学习率 ¶

尝试使用不同的学习率，观察损失函数值下降的快慢。

学习率过大前期损失值下降快，但是后面不容易收敛 学习率太小，损失函数下降慢

调学习率的一些心得 1. 选择对学习率不太敏感的算法：Adam 2. 合理的参数的初始化

学习率设置过大会导致梯度爆炸的问题

收敛判断 | epoch ¶

• 真实训练中，凭直觉
• 先训练小批次

overfitting | 过拟合 ¶

在测试集上效果好的模型就是好的模型

在测试集上效果差的模型就是差模型

把 training data 中的 noise 也学习到了

• Ridge Regression | 岭回归

Loss(omega*)

regularization: 一些先验的假设，比如 \(\omega\) 是稀疏的，或者 \(\omega\) 是平滑的；避免学习到

超参数： - \(\lambda\)：控制正则化的强度: \(\lambda\)越大，正则化的强度越大，模型越简单，training error 越大；如下图，左侧叫做过拟合，右侧叫做欠拟合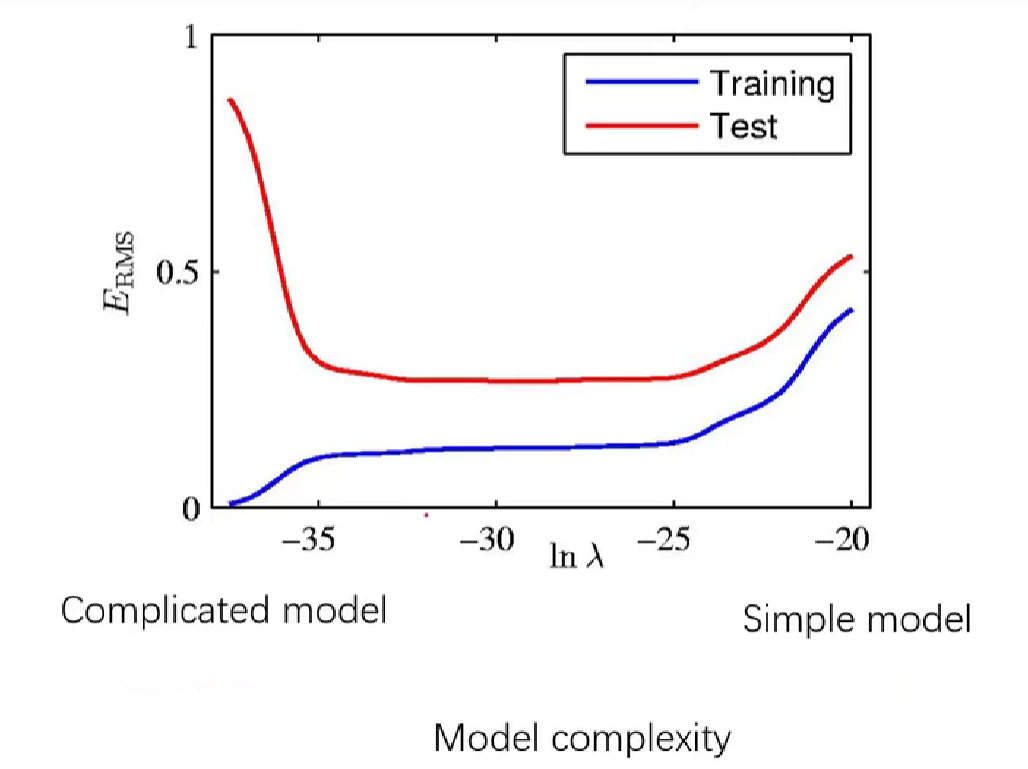 - \(\alpha\)：控制学习率

神经网络需要学习一些噪声：batchsize 小一点有时候不是坏事 采用dropout的方法

教小孩的时候不能一直夸奖

Logistic Regression¶

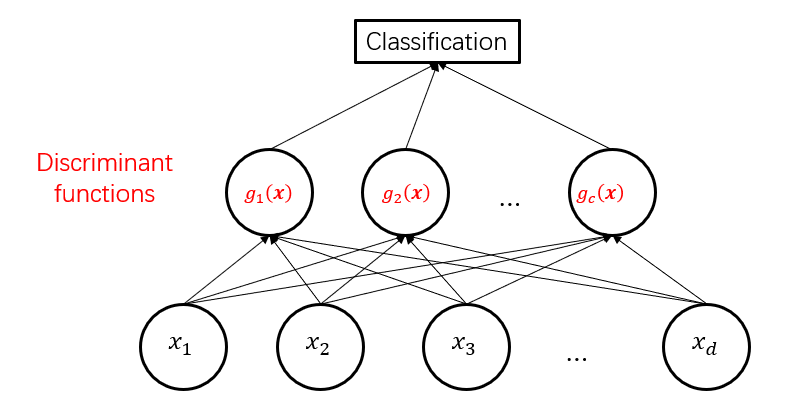
线性回归有一个很强的假设，就是 y 是连续的；并且有更像邻近数的趋势 (MSE 对于线性回归不是一个好的 function)

• one vs. Rest

logistic function:

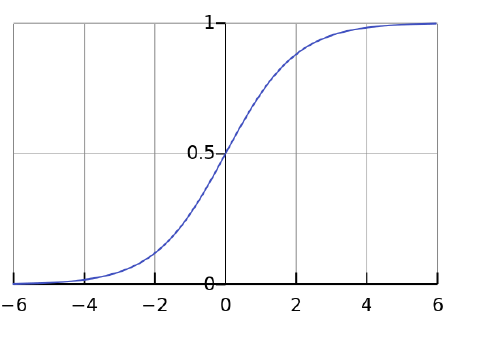
• sigmoid function: \(f(x) = \frac{1}{1+e^{-x}}\) CDF(累积分布函数)ofthe standard logistic distribution
  使用sigmoid函数将线性回归的输出转换为概率

为什么 loss function 要取 log - 为了方便求导 - 取log使得连乘变成连加，不会丢失信息

Assumptions behind logistic regression - l(a) = -sum_{iin I} log(1+e^{-y_i a^T x_i})

pros: - binomial distribution is a good assumption for classification - provide a probability - low computation, easy to optimize - support online learning:梯度下降的模型都支持在线学习

cons: - too simple:high bias & low variance

对于分类问题，只关心分类正确的类的值

LDA¶

理解主成分分析（1）——最大方差投影与数据重建 - Fenrier Lab

简单理解线性判别分析 - 知乎

LDA 线性判别分析——投影的疑问解答 _lda 投影 -CSDN 博客

最小化类内方差

最大化类间方差

因为自变量只有 \(w\)，不一定二者都能同时达到最优，所以整合到一起取下式的最大值：

LDA——线性判别分析基本推导与实验 -CSDN 博客

二分类线性判别分析，看懂这篇就够了 - 知乎