Uninformed Search¶

约 1317 个字 52 行代码预计阅读时间 6 分钟

评判标准	广度优先 (BFS)	深度优先 (DFS)	有限深度 (DLS)	迭代加深 (IDS)
简单表述	从最浅节点开始扩展，探索所有可能性。序列为先进先出	一条路径一直向下扩展，没有节点可以扩展就向前回溯，序列为先进后出	在 DFS 基础上限制深度在一个常数 \(l\)，防止过深。	逐步增加深度限制 \(l\)
完备性 ( 是否有解 )	Yes	No	Yes, if l ≥ d	Yes
最优性（是否最优解）	No/Yes	No	No	No/Yes
时间复杂度	\(O(b^{d+1})\)( 最深一层 )	\(O(b^m)\)	\(O(b^l)\) ( 深度限制 )	\(O(b^d)\)
空间复杂度	\(O(b^{d+1})\)	\(O(b^m)\)	\(O(b^l)\)	\(O(b^d)\)

注：DFS 不完备是因为可能陷入无穷循环，不满足最优性是因为默认 - b: branching factor, 每个节点可以扩展的子节点数 - d: solution depth, 解的深度(最优解在的深度) - m: maximum depth, 整个搜索空间的最大深度

目标形式化：“成功“的状态描述
问题形式化：根据所给的目标考虑行动和状态的描述
搜索：通过对行动序列代价计算来选取最佳的行动序列
执行：给出”解“执行行动

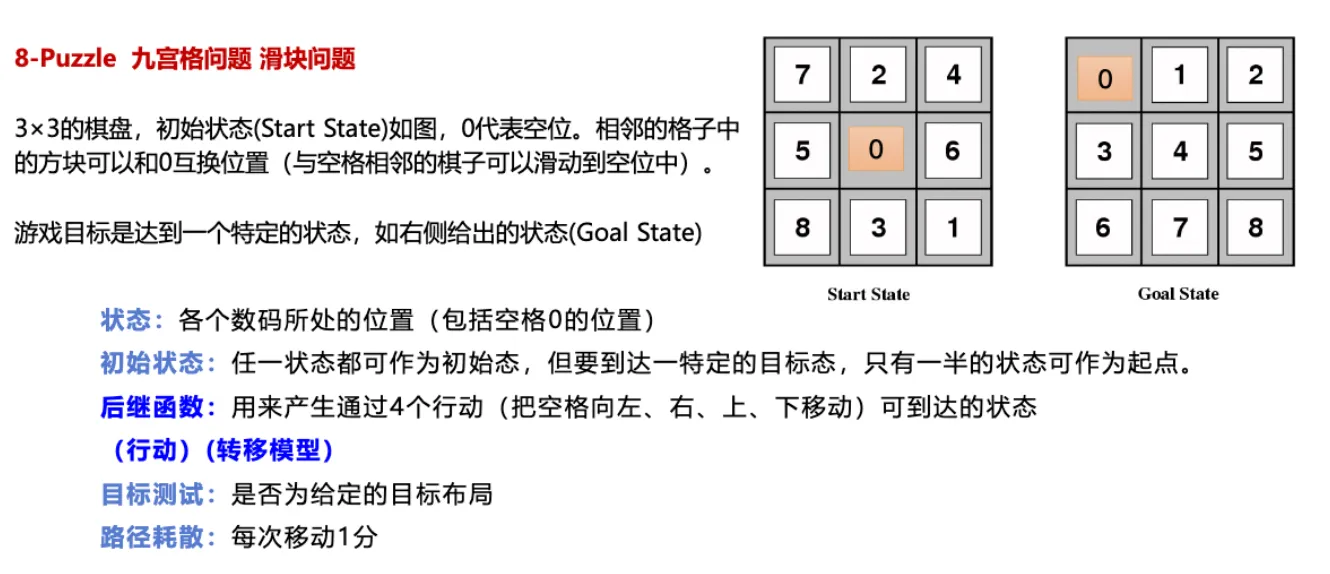
良定义的问题及解：

良定义问题五要素：初始状态、可能行动、转移模型、目标测试函数、路径耗散函数。
问题环境用状态空间表示，状态空间中从初始状态到目标状态的路径是一个解。

搜索基本概念 ¶

图搜索与数搜索

状态图搜索：

搜索：从初始节点出发沿着与之相连的边试探地前进，寻找目标节点的过程
搜索树：搜索过程中经过的节点和边按照原图的连接关系会构成一个树
解：搜索过程中搜索树会不断增长，直到搜索树中出现目标节点，搜索便停止

两个表：

CLOSED 表：记录考察过的节点
OPEN 表：登记当前待考察的节点

图搜索：树搜索 +explored set

BFS¶

Breadth-first Search （宽度优先搜索）

可以实现两类问题

从节点 A 出发，有前往节点 B 的路径吗
从节点 A 出发，前往节点 B 的哪条路径最短

Search Strategy （搜索策略）：扩展最浅的未扩展节点。 Implementation（实现方法）：使用FIFO队列，即新的后继节点放在后面。

Breadth-first Search Algoruthm on a Graph （图的宽度优先搜索算法）

数据结构——队列 ¶

数据结构：队列（Queue）像排队一样，先进先出（FIFO）。

你从一个起点开始，先查看所有“邻居”（直接相连的点）。再从这些“邻居”出发，查看它们的“邻居”，一层一层地扩展。

Uniform-cost Search （一致代价搜索）¶

是对广度优先搜索算法的引伸，扩展路径消耗 \(g(n)\) 最低的节点。即 \(f(n) = g(n)\) 即启发式搜索的效用函数，是当前路径的评价指标。

使用优先级队列储存边缘

当每个边缘有不同的成本时，该算法开始起作用。

完备性、最优性：零代价行动时可能陷入死循环，如果每一步的耗散都大于等于某个正值常数则能保证完备性和最优性
时间、空间复杂度：由路径代价而不是深度来引导，引入 C 表示最优解的代价。若每个行动的代价至少为 e，那么最坏情况下算法时间和空间复杂度为 \(O(b(1+[C/e]))\)

性能分析 ¶

DFS | 深度优先搜索 ¶

类似于“不撞南墙不回头”

BFS 常用于找单一的最短路线，它的特点是 " 搜到就是最优解 "，而 DFS 用于找所有解的问题，它的空间效率高，而且找到的不一定是最优解，必须记录并完成整个搜索，故一般情况下，深搜需要非常高效的剪枝（剪枝的概念请百度）。

数据结构——栈（stack）¶

像装箱子一样，后进先出（LIFO）。过程：从一个起点开始，你沿着一条路走到底，直到不能走了为止。然后返回上一个分叉点，尝试另一条路。重复直到所有路径都走过。

DFS 递归模板——使用系统栈

boolean DFS(Node cur, Node target, Set<Node> visited) {
    return true if cur is target;
    for (next : each neighbor of cur) {
        if (next is not in visited) {
            add next to visted;
            return true if DFS(next, target, visited) == true;
        }
    }
    return false;
}

DFS 栈模板

boolean DFS(int root, int target) {
    Set<Node> visited;
    Stack<Node> s;
    add root to s;
    while (s is not empty) {
        Node cur = the top element in s;
        return true if cur is target;
        for (Node next : the neighbors of cur) {
            if (next is not in visited) {
                add next to s;
                add next to visited;
            }
        }
        remove cur from s;
    }
    return false;
}

性能 ¶

完备性：有限空间中完备；无限深度空间中不完备
最优性：No
时间复杂性：\(O(b^m)\)，m 为状态空间中路径的最大长度
空间复杂性：\(O(bm)\)，线性空间

DLS | Depth-limited Search （深度受限搜索）¶

若状态空间无限，深度优先搜索就会发生失败。这个问题可以用一个预定的深度限制\(l\)得到解决，即：深度\(l\)以外的节点被视为没有后继节点。缺点：如果我们选择\(l<d\)，即最浅的目标在深度限制之外，这种方法就会出现额外的不完备性。如果我们选择\(l>d\)，深度受限搜索也将是非最优的。

Iterative Deepening Search （迭代加深搜索）¶

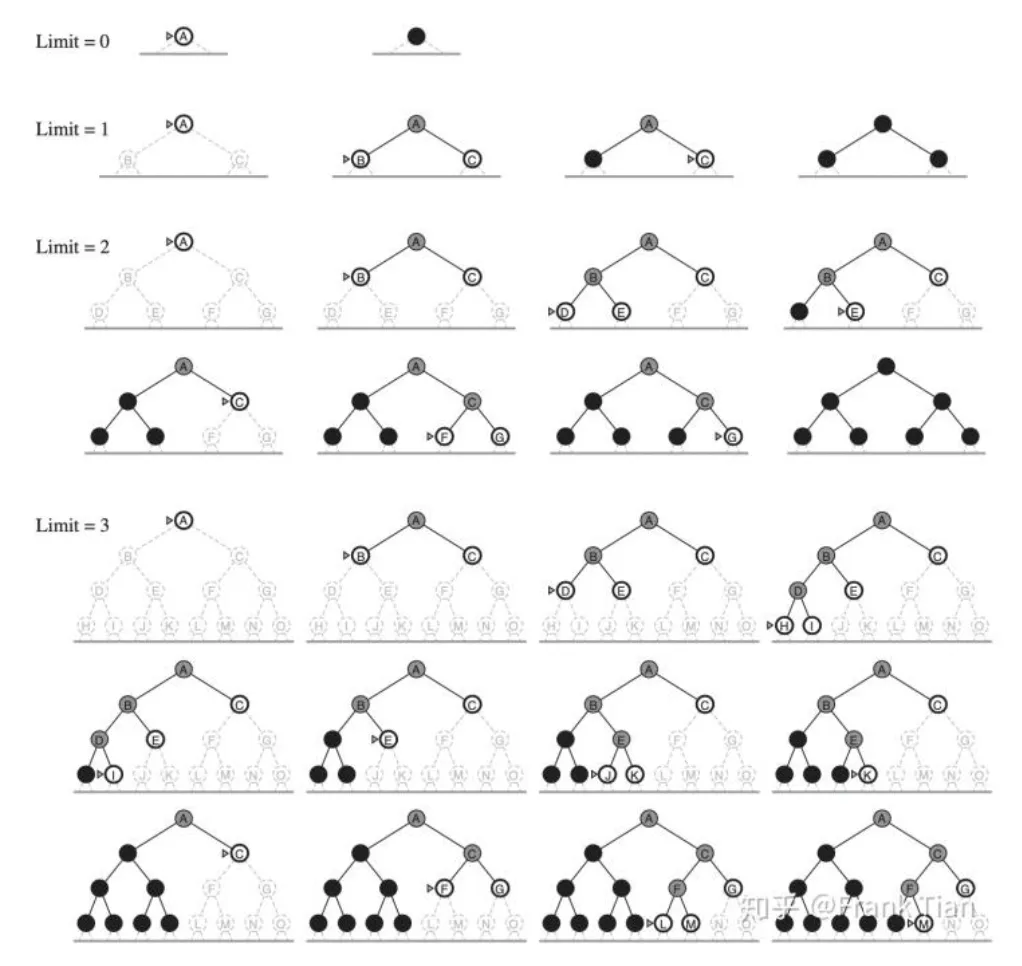一般来说，当搜索空间很大且解的深度未知时，迭代加深搜索是首选的盲目搜索方法

例题 ¶

全排列 ¶

DFS 全排列

#include <iostream>
int number[10]={0,1,2,3,4,5,6,7,8,9};
int num[10];
bool vis[10]={0};
void dfs(*int num,int n){
    if (n==10){
        for (int i=0;i<10;i++){
            cout<<num[i];
        }
        cout<<endl;
        return;
    }
    for(int i=0;i<10;i++){
        if (!vis[i]){
            vis[i]=1;
            num[n]=number[i];
            dfs(num,n+1);
            vis[i]=0;
        }
    }
}
int main(){ 
    dfs(num,0);
    return 0;
}

Bidirectional Search （双向搜索）¶

实际上，BS 就是将 BFS 画的半径为 d 的一个大圆，换成了半径为 d/2 的两个小圆。